AutoCAD与ParaSolid三维边界模型信息直接交换

张应中， 罗晓芳， 乔 磊

（大连理工大学机械工程学院，辽宁 大连 116024）

AutoCAD与ParaSolid三维边界模型信息直接交换

张应中， 罗晓芳， 乔 磊

（大连理工大学机械工程学院，辽宁 大连 116024）

对 ACIS和 ParaSolid的三维实体边界表达数据结构进行分析，基于DwgDirect接口技术，直接打开AutoCAD的DWG文件，对AutoCAD的DWG文件中基于ACIS的三维实体边界信息遍历，获取实体边界的拓扑信息和几何信息；基于ParaSolid提供的API开发函数，通过实体拓扑构造、实体几何构造和几何与拓扑附属关联，实现AutoCAD与ParaSolid三维边界模型的直接交换。最后给出一个直接交换实例。

计算机应用；AutoCAD；ParaSolid；三维边界模型；直接交换

AutoCAD是目前应用最广泛的二维CAD平台，AutoCAD从R11开始具有三维实体模型，从 R13开始采用 ACIS几何核心来构造三维实体，随着版本不断升级，三维造型功能日益强大，并且得到广泛的应用。ParaSolid是目前国际上最为成熟，应用最广的几何造型内核，CAD中著名的 UG、SolidWorks、SolidEdge等都是以ParaSolid作为几何造型内核；CAM和CAE中大部分软件系统都支持 ParaSolid的数据格式。研究和实现AutoCAD与ParaSolid三维边界模型信息交换有重要的实际意义。

异构环境下，三维边界模型信息交换方法目前普遍采用的是基于中间文件[1-2]，为此制定和形成一些国际标准和行业标准，例如 IGES、DXF和STEP等。基于中间文件交换要求系统具备能生成符合标准的中间文件功能，并且存在信息丢失，操作烦琐，效率低问题，由于AutoCAD系统的支持信息交换能力不强，造成基于AutoCAD系统的三维实体信息资源不能实现有效的交换。

本文基于DWGDirect技术，直接打开DWG图纸，搜索和遍历AutoCAD中基于ACIS的三维实体边界几何和拓扑信息，通过 ParaSolid的边界拓扑映射，直接生成 PrarSolid三维边界实体，实现AutoCAD与ParaSolid三维边界模型的直接交换。

1 三维边界模型信息表达

1.1 实体边界表达模型

边界表达(B-reps)是三维实体模型最基本的表达方法，是将形体表达为它的有限数量的边界表面的集合。表面可能是平面，也可能是曲面，每个表面又可用它的边界的边及顶点表示。B-rep中信息分为两类：一类是几何数据，描述形体的大小、尺寸、位置、形状等；另一类是拓扑信息，拓扑是研究图形在形变与伸缩下保持不变的空间性质的一个数学分支。拓扑只关心图形内相对位置关系，不问它的大小与形状。在B-rep中拓扑信息是指用来说明体、面、边及顶点之间连接关系的一类信息。

1.2 PreaSolid 边界表达模型

ParaSolid 是美国UGS公司的一个业界领先的几何实体建模内核，其拓扑实体定义如下[3]：

（1） 体(Body) 体是ParaSolid中一种基本形体，可以由一个或多个简单形体连接组合而成。它有以下几种形式：Acorn：孤立点，Wire：线框，Sheet：薄板，Solid：立体，General：一般形体。

（2） 区域(Region) 区域是一个开放的三维空间的连通子集，它的边界是一系列的点、边和有向面。

（3） 壳(Shell) 壳是一系列有向面和边的集合，面的一面或双面都可以被外壳引用。外壳的组成：面和方向逻辑的集合；边的集合；单个的顶点。

（4） 面(Face) 是一个曲面的有界集合，它的边界是若干个环，是一个二维的区域。边界为零个环的面构成一个封闭的实体，如一个球面。

（5） 环(Loop) 是一个面的边界，是一个连接的二维实体。一个环在一个方向上不能通过一条边两次。环的方向是这样规定的：沿该环的方向前进，面在左边。

（6） 翼(Fin) 表示一条边在环中的方向。它包含两个数据：一个是逻辑值，表示边与环是否同向；另一个数据是在该条边具有不同的局部精度时，边所依附的曲线。

（7） 边(Edge) 是一条曲线上有界的一段，它的边界是零个、一个或两个顶点。边是一个一维区域。

（8） 顶点(Vertex) 顶点表示空间中的一个点，是一个零维的区域。

ParaSolid几何实体分为基本几何实体和构造几何实体，都具有三种类型：Surface曲面、Curve曲线和Point点。Surface曲面主要依附于拓扑 Face面，典型曲面有：平面、圆柱面、圆锥面、圆环面、球面、过渡曲面、样条曲面、异构几何曲面、偏移曲面、扫描曲面和旋转曲面；Curve曲线主要依附于拓扑 Edge边，典型曲线有：直线、圆、椭圆、B样条曲线、一般样条曲线、异构几何曲线。

基本几何实体依附在对应的拓扑体上，构造几何实体是新创建的还没有附属关联的几何实体，都可以表达为Body体。ParaSolid几何实体与拓扑实体关系如图1所示。

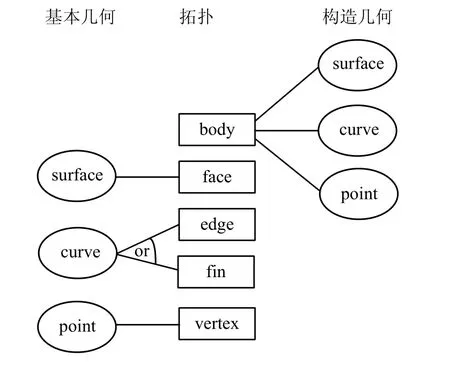
图1 ParaSolid几何实体与拓扑实体关系

1.3 ACIS边界表达模型

ACIS是美国 STI公司(Spatial Technology Inc.)推出的具有开放式软件体系结构的实体造型软件开发平台。ACIS的边界模型也是表达为拓扑表示和几何表示，拓扑结构按层次从上到下分解成下列对象[4]：体(Body)、块(Lump)，表示空间一个有边界的相互连通的区域；壳(Shell)、面(Face)、环(Loop)、有向边(Coedge)、边(Edge)、顶点(Vertex)。其几何表达类型和拓扑信息关系与上述ParaSolid基本类似。

2 DWG中的 ACIS三维模型边界信息的提取

AutoCAD图形保存的缺省文件是 DWG文件，DWG是一个压缩格式未公开的二进制格式文件，目前CAD图纸绝大部分是以DWG格式存贮。能直接打开DWG图纸，并且能搜索和遍历出ACIS三维边界几何和拓扑信息是实现直接交换的基础。

DWGdirect是由开放设计协会(Open Design Alliance)推出的用于独立于 AutoCAD平台之外访问DWG文件接口，目前已被国际上众多公司所接受。本文采用 DWGdirect接口访问和搜索DWG文件中基于ACIS的三维实体边界几何和拓扑信息。

2.1 DWG中三维实体元素

在DWGDirect中，DWG文件的图形实体数据在内存中由一个 OdDbDatabase类的实例表示[5]，并且提供了一个可以访问其图形数据库实体对象的块表记录遍历迭代器(OdDbBlock TableRecordIterator)，通过该迭代器可以遍历存储在块表空间中的各种实体图形，如二维的直线段、圆弧、圆，三维的圆柱面、圆锥面、球面和三维实体等。

三维实体元素是OdDb3dSolid类一个实例，OdDb3dSolid类是从 OdDbEntity类派生而来，OdDbEntity类是数据库实例中所有绘图对象的基类。同时，在DWGdirect中还提供了一个通用几何类 OdGe类和用于边界表示的 OdBr类。OdGe类是用来实现2D和3D几何对象操作的。OdBr库是一个边界表示库，允许用户以只读的方式去访问ACIS所创建的用边界表示法表示的实体，这类实体指的是OdDb3dSolid类的对象。

2.2 DWGdirect的三维实体边界定义

OdBr库中提供了一个用来定义实体边界表示的拓扑对象的接口类OdBrEntity。它的结构层次如图2(a)所示。OdBrEntity类是Brep结构抽象类；OdBrBrep类是Brep实体边界类，它是提供在OdDb3dSoid实体中对ACIS实体数据的Brep结构进行遍历的最高层。

OdGe库中提供一个OdGeEntity3d类，它是所有OdGe类的几何对象的基类。它的结构层次如图2(b)所示。

2.3 实体边界数据获取

DWGdirect定义一个访问ACIS边界数据结构的接口 OdBrBrep类，通过 OdBrBrep为OdDb3dSolid实例对象和ACIS边界之间建立联系。同时还定义了遍历访问ACIS边界拓扑结构的遍历器(traverser)类，可以遍历访问ACIS边界的壳、面、环、边、点拓扑信息和几何信息。对每一个OdDb3dSolid三维实体对象，其实现步骤如下：

（1） 创建 OdBrBrep实例对象，通过OdDb3dSolid类的成员函数 brep (OdBrBrep&brep)赋值；

（2） 定义拓扑遍历器，自顶向下遍历ACIS边界拓扑结构树。拓扑遍历器的定义是按照壳、面、环、边、点自上而下拓扑顺序分别定义，即通过OdBrBrep实例定义壳拓扑遍历器，拓扑遍历三维实体对象所有壳拓扑，通过壳拓扑信息定义面拓扑遍历器，拓扑遍历壳对象所有面拓扑信息，通过面拓扑信息定义环拓扑遍历器，拓扑遍历面对象所有环拓扑信息，依次遍历下去，从而获取实体边界所有拓扑和几何信息。

图2 DWGdirect 实体边界表示结构

3 ParaSolid实体边界映射构造

ParaSolid采用与ACIS相类似的实体边界表示，同时ParaSolid提供一个API函数，可以直接构造出 ParaSolid实体的拓扑结构。尽管ParaSolid与ACIS实体边界表示有些差别，通过拓扑映射的方式，完全可以将上述获取的 ACIS边界数据通过以下步骤重新构造出 ParaSolid实体边界。

实体边界映射构造主要涉及三个步骤：拓扑构造；创建几何数据；关联拓扑与几何数据。为了保证几何造型的可靠性与正确性，构造的实体要满足正则拓扑实体的要求：正则形体不能有悬边、悬线、悬面等等，同时还需要精度误差进行控制。

3.1 拓扑构造

3.1.1 ParaSolid拓扑构造API函数

在ParaSolid中提供了一个拓扑构造API函数PK_BODY_create_solid_topology，用来创建实体的拓扑。函数的具体形式是[3]：

上述参数中classes[ ]数组描述构造那些拓扑实体，拓扑实体类型通过 PK_CLASS_body，PK_CLASS_shell， PK_CLASS_face，PK_CLASS_loop， PK_CLASS_edge，PK_CLASS_vertex表达体、壳、面、环、边和点。

parents[ ]、children[ ]和 senses[ ] 三个数组定义拓扑元素父子之间的关系，例如壳面关系、面环关系、环边关系等。通过拓扑元素父子之间的关系定义，将classes[ ]数组描述构造的拓扑实体关系联系起来，形成完整的实体拓扑结构。

拓扑元素及父子关系的选用按如下规则：

（1） 当体具有多个（大于1）壳拓扑时，外壳必须第一个定义；

（2） 环的子边必须按绕环顺序定义；边的子点必须按边的方向定义；

（3） 每个边作为子类必须被使用两次，每个拓扑关系一次；

（4） 一个环类必须以多个边类或者单个点作为子类，但不能以边和点混合或者多个点作为子类；

（5） 一个点类必须以多条边或单个环作为父类，其父类不能为边与环的组合或者多个环。

例如，一个方块体含有 33个拓扑(n_topols=33)，其中包括1个壳，6个面，6个环，12条边和 8个顶点。实体拓扑之间的关系共有60个，1个壳是由6个面组成，壳面关系为6；每个面由1个环组成，面环关系为6；一个环由4条边组成，环边关系为24；每条边由2个顶点组成，边顶点关系为24。parents[0]～parents[5]指向壳拓扑元素在在 class数组中序列号，此处全为 0；children[0]～children[5] 指向面拓扑元素在class数组中序列号，分别是1、2、3、4、5、6。senses[]定义了每两个拓扑实体之间的方向关系。当子类为边 PK_CLASS_edge，且当子类边在父类环的相同方向时，senses被赋值为PK_TOPOL_sense_positive_c；当子类边在父类环的相反方向时，senses被赋值为PK_TOPOL_sense_negative_c；其他情况下senses被赋值为PK_TOPOL_sense_none_c。

3.1.2 拓扑构造实现

拓扑构造实现的算法步骤如下：

（1） 计算要创建的拓扑体的个数

根据上述对ACIS边界拓扑遍历，计算出壳的个数、面的个数、环的个数、边的个数和点的个数之和。

（2） 设置各个拓扑体的类型

根据计算的拓扑体个数，分配拓扑体的类型数组空间，并根据拓扑类型设置相应数组位置拓扑类型值，例如一个体有一个壳，classes[0] =PK_CLASS_shel；一个壳有 6 个面，则 classes[1]～classes[6]=PK_CLASS_face。数组元素中下标变量Index和classes[Index]值确定了所构造的拓扑结构数组中第Index的拓扑类型。

（3） 计算拓扑体元素关系个数

根据上述 ParaSolid对拓扑体元素关系定义规则及ACIS边界拓扑遍历结果，计算拓扑体元素关系个数n_relations。

（4） 设置拓扑体元素关系

根据计算的扑体元素关系个数，分配拓扑体元素关系数组空间，即 parents[ ]、children[ ]和senses[ ]设置为同样大小的数组。并根据拓扑类型设置相应数组位置拓扑元素关系值。

3.2 几何构造

3.2.1 ParaSolid几何定义

ParaSolid几何实体有三种类型：Surface曲面、Curve曲线和Point点。Surface曲面类型有平面、圆柱面、圆锥面、圆环面、球面、过渡曲面、样条曲面、异构几何曲面、偏移曲面、扫描曲面和旋转曲面；Curve曲线主要有：直线、圆、椭圆、B样条曲线、一般样条曲线、异构几何曲线。

例如，圆柱面是通过一个三维点，圆柱面轴线方向矢量，参考方向矢量以及圆柱面的底面半径的数据结构定义：

3.2.2 几何创建

重新开始对ACIS边界拓扑遍历，重设拓扑定位指针变量 Index=0；并依壳、面、环、边、点的顺序，获取相应附属拓扑元素的几何信息，创建相应的几何实体，每遍历一个拓扑元素，拓扑定位指针变量Index加1。

ParaSolid提供针对具体各曲面、曲线和点实体构造的API函数。设置一个数据结构保存构造的几何实体和该几何实体相附属的拓扑定位指针，例如曲面实体保存数据结构如下：

3.3 几何与拓扑关联

一个有效的实体应该是具有完整的拓扑与几何信息数据，上面步骤所完成的只是一个分离的拓扑实体和几何实体，需要将其有机地关联系起来。

通过 PK_BODY_create_solid_topology函数成功完成拓扑构造后，返回已经创建的拓扑体存放在一个数组变量topols中，topols按照输入的顺序存放拓扑元素，即构造的拓扑体顺序与class[ ]数组中的顺序是一致的，这就为构造几何体与其对应拓扑关联创造条件。

ParaSolid 提供几何体与其对应拓扑关联的API函数。PK_FACE_attach_surfs函数关联曲面几何到Fcae面拓扑，PK_EDGE_attach_curve函数关联曲线几何到 Edge边拓扑，PK_VERTEX_attach_pointe函数关联点几何到Vertex点拓扑中。

4 交换应用实例

上述AutoCAD与ParaSolid三维边界模型的直接交换方法在作者开发的JhSolid2007下实现。JhSolid2007采用ParaSolid作为几何造型内核，VC++、OpenGL开发。基于DwgDirect接口，可以直接打开AutoCAD具有三维实体的DWG文件，将AutoCAD中的三维实体，在JhSolid2007下作为引入几何体生成。图3是一个交换的简单零件实例。

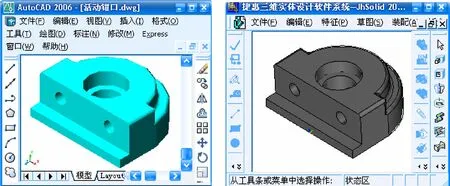
图3 交换零件实例

5 结 束 语

本文通过对AutoCAD中基于ACIS的三维实体边界表达数据结构和 ParaSolid的三维实体边界表达数据结构的分析，基于DwgDirect接口技术和ParaSolid提供的API开发函数，通过对ACIS的三维实体边界遍历，获取实体边界的拓扑信息和几何信息，通过拓扑构造、几何构造和几何关联，实现AutoCAD与ParaSolid三维边界模型的直接交换。为AutoCAD系统下三维实体信息资源的充分利用创造条件。

本文介绍的三维边界模型的直接交换方法对基于ParaSolid几何造型内核的UG、SolidWork等软件系统的二次开发实现直接读取DWG的三维实体信息也有一定的参考意义。

[1]Pratt Michael J, Anderson Bill D, Ranger Tony.Towards the standardized exchange of parameterized feature based CAD models [J]. Computer-Aided Design, 2005, 37 (12)：1251-1265.

[2]陈小安, 谭 宏. 三维几何模型的中性文件格式的数据交换方法研究[J]. 机械工程学报, 2001, 37(10)：93-99.

[3] Unigraphics Solutions Inc. ParaSolid online documentation [M/CD]. Unigraphics Solutions Inc,2000.

[4]赵建军, 王启付. 基于边界表达的ParaSolid与ACIS直接双向接口[J]. 计算机工程, 2004, 30(8)：40-41.

[5]Open Design Alliance. DWGdirect reference [M/CD].Open Design Alliance, 2003.

Direct Exchange of Three-dimensional Boundary Model Information between AutoCAD and ParaSolid

ZHANG Ying-zhong, LUO Xiao-fang, QIAO Lei
( School of Mechanical Engineering, Dalian University of Technology, Dalian Liaoning 116024, China )

The data structures of the three-dimensional solid boundary expression for ACIS and ParaSolid are analyzed, based on DwgDirect interface technology DWG files in AutoCAD are directly opened and the three-dimensional entity boundary information based on ACIS in AutoCAD's DWG file are searched and accessed. Based on the API development function provided by ParaSolid, by means of constructing topology entities, constructing geometry entities and associating geometry entities to topology entities procedures, the accessed boundary topology and geometry information can be directly exchanged to construct a solid model based on PrarSolid. Thus direct exchange of three-dimensional boundary model information between AutoCAD and ParaSolid is realized. At last an example of direct exchange is given.

computer application; AutoCAD; ParaSolid; three-dimensional boundary model;direct exchange

TP 391

A

1003-0158(2010)05-0169-06

2009-04-08

国家自然科学基金资助项目（60773214）

张应中（1961-），男，湖南绥宁人，副教授，博士，主要研究方向为计算机辅助设计，产品数字建模及处理技术。