轴力作用下K型焊接管节点的应力集中系数分析
2010-09-22邵永波
邵永波
(烟台大学土木工程学院,山东 烟台 264005)
1 引 言
K型管节点广泛应用于海洋平台结构中。在支承海洋平台的管状结构中,节点处通常是研究者最关注的部位,因为大多数管状结构的破坏主要是由节点处的破坏所引起的。海洋平台中的管节点结构主要承受由海浪和风造成的循环荷载,所以节点处易发生疲劳破坏。管节点的疲劳破坏主要表现为在焊缝处产生表面裂纹,表面裂纹的扩展会产生两方面的影响:一是造成节点结构在焊缝处的刚度降低,从而降低了节点结构的极限抗载能力,尤其是裂纹穿透管壁后,其扩展速度非常快,节点在焊接处容易产生断裂破坏,造成很严重的工程事故;二是表面裂纹穿透管壁后,管道内部的石油或者天然气会发生泄露,造成海面的污染。因此,应确保海洋平台结构在使用年限内不发生疲劳破坏。
在研究管节点疲劳寿命的时候,国内外经常使用的方法是参照S-N曲线,即通过计算管节点在焊缝处的热点应力大小来估计节点所能承受的疲劳载荷的循环次数。在估算焊缝周围的热点应力的时候,经常采用的方法是计算节点在承受不同载荷作用下的应力集中系数。国内钢结构设计规范(GB50017)中尚无提供对管节点应力集中系数的计算方法。国际上比较通用的计算管节点应力集中系数的设计规范是CIDECT[1]。但CIDECT中有关管节点应力集中系数的计算方法并不完善,需要根据节点的几何参数参考一定的曲线来确定节点的应力集中系数。这在工程设计中是不方便的,而且从曲线上读取数据也容易产生比较大的误差。国内对管节点应力集中系数的研究在80年代末就开始了,并已经取得了一些研究成果,如文献[2-6]。但是这些结果基本上是用试验或者有限元对某类型的节点进行测试或者计算。并没有提出一种简单适用的计算管节点应力集中系数的方法,所以很难应用到工程设计中去。如何提出另外一种更方便地应用于工程设计中的节点应力集中系数的计算方法是国内外很多研究者所感兴趣的。本文就是通过有限元分析和试验测试相结合,研究轴力作用下K型管节点焊接处应力集中系数的计算方法。
通常K节点的应力集中系数是由其几何参数、载荷形式、焊缝尺寸和边界条件等多种因素决定。工程中的K节点承受的最普通的载荷类型是轴向力(通常是一个支管受拉,另外一个支管受压)。K节点主管两个端部可以看成是固支的。因此,在研究K节点应力集中系数的时候,基本上集中在其几何参数和焊缝尺寸的影响上。研究如何模拟焊缝尺寸以及调查K节点几何参数对其应力集中系数的影响是精确估算K节点应力集中系数的主要因素。
2 KK型管节点焊缝的模拟方法
KK管节点是通过把四个支管焊接到主管外表面而形成的。支管和主管之间的交线在空间上是一条形状非常复杂的曲线。Cao等(1997)[7]提出了这条相交曲线的方程,为模拟焊缝提供了理论上的可行性。以前对管节点的研究经常采用两种假设:一是假定管壁的厚度与管的直径相比是很小的,因此忽略管壁厚度方向上应力的变化而把管壁看成一个曲壳;二是忽略焊缝对管节点应力集中系数的影响。这两个假设都过低地估计了管节点的几何刚度,从而会过高地估计焊缝处应力集中的程度。所以以前用于计算管节点应力集中系数的方法(如CIDECT)在工程设计中都是偏于保守的。为了更精确地计算管节点的应力集中系数,就必须考虑焊缝的影响。

在不考虑焊缝的情况下,支管和主管的内部和外部交线如图1a和1b中的实线所示。考虑焊缝的时候,支管和主管实际上的内外部交线如虚线所示。外部交线将向外移动一段距离T2,而内部交线则移动T3的距离。不考虑焊缝的时候,支管和主管初始的接触厚度为T1,如图1b所示。
通常T1沿着交线的大小是发生变化的,其大小取决于图2所示的两面角的大小和主管的曲率大小。一般情况下,支管厚度tb是要远小于主管半径R1的,这种情况下,T1的大小接近于tb/sin()γ 。
为模拟焊趾W0(如图1所示),可以从两管交线上一点A0向外延伸一段距离T2。沿着主管和支管的交线,T2随二面角γ0的不同而变化。角度γ0的变化范围是从假设主管和支管之间夹角θ的最小值(工程中的K节点中,此夹角的最小值大约为30°)到180°。T2的大小可以通过下面的公式计算:


其中,T2是外部焊缝厚度,k2是外部交线修正因子,FOSouter是比例因子,m是一个常数,θs是主管和支管之间的最小夹角。
经过修正以后,焊趾部分的外部交线方程可以写成如下形式:
其中,φ0为焊缝法线方向与主管轴向之间的夹角。
在公式(3)中,点 A0(XA0,YA0,ZA0)是外部交线上一点,点B0是由点A0沿支管方向移动(T1+T4)而得到的,如图3a和3b所示。

按照相同的方法,内部相交线上的点Ai到焊跟Wi的距离为T3,如图3所示。二面角γi的范围是从30°到 90°。 当 γi=30°时 T3取极大值,而当 γi=90°时 T3=0。 T3可以表示为如下形式:

其中,T3是外部焊缝厚度,k3是外部交线修正因子,FOSinner是比例因子,n是一个常数,θs是主管和支管之间的最小夹角。
经过修正以后,焊跟部分的内部交线方程可以写成如下形式:

管节点的焊接厚度Tw是由T1,T2和T3共同决定的,且必须满足有关规范(如AWS,2000[8])规定的焊缝厚度的最小要求。Tw可表示为:

其中kaws是由AWS(2000)[3]规范规定的焊缝厚度参数。
3 KK管节点有限元网格的产生
3.1 单元类型的选择
以往对管节点进行数值模拟时,基本上采用的是壳单元。这是由于大部分管节点的壁厚大小远小于其直径的原因。而且先前的研究工作中往往忽略了焊缝尺寸对管节点应力集中系数的影响。但是,壳单元在模拟管节点时有两个很难克服的缺点:一是在管壁厚度与直径相比不是非常大的情况下,应力沿着壁厚方向的变化难以反应出来;二是难以比较精确地模拟焊缝形状。Lee和Bowness[9]通过对管节点的研究发现管壁内外表面的应力大小并不相同,这种差异是由于管壁内的弯曲应力造成的。为了克服壳单元在模拟管节点上的缺陷,Herion等[10]通过研究提出了三维二次实体单元是最适合模拟带焊缝节点的单元。在本研究中,这种20结点的二次单元也被采用来模拟带焊缝的K节点。
3.2 有限元网格的产生原理和方法
采用有限单元法对结构进行分析时,所得到的数值结果的精度在很大程度上取决于所采用有限元网格中单元的质量和数量。所谓单元的质量是指在有限元网格中划分的单元不能过度扭曲,尤其是在应力梯度比较大的区域单元的边长比例不能太大。单元的数量是用来保证有限元结果的收敛性。在对一个结构进行有限元分析时,往往关心的是应力梯度高的区域,因为这个区域一般是结构发生破坏的地方。因此,在高应力梯度的区域,有限元网格可以划分得精密一些,而且应该控制这个区域的单元质量。反之,低应力区一般是结构分析中不关心的区域,为了提高计算效率,这个区域的网格划分可以相对粗糙一些,而且对单元质量的要求也不必太高。
根据以上原则,可以根据计算精度的要求,将整个K节点结构分成不同的区域,在每个区域单独进行网格划分。由于热点应力位于焊缝位置处,这个位置应力集中很严重,所以焊缝位置的网格划分需要精密,而且单元质量要求高。远离焊缝的区域对K节点应力集中的影响比较小,在这些区域可以采用比较粗糙的网格以减少计算时间。按照这个标准,整个K节点可以划分为几个不同的区域,如图4a所示,这几个区域的网格均单独生成。当每个区域网格生成以后,K节点的整体有限元网格可以通过合并各个区域的网格而得到,如图4b所示。
采用分区法产生K节点有限元网格可以保证焊缝处的网格的高质量,同时也保证这个区域网格密度大。在焊缝区域,沿着管壁厚度方向上共划分了三层单元。为了验证有限元结果的收敛性,本研究中提出了一种K节点网格自动加密方案。在这个方案中,每个单元的每条边都被平均分成两份,这样一个母单元被平均分成8个子单元。经过这样加密后的网格中单元数量是初始网格中单元数量的8倍。图5a中显示了焊缝区域的网格的加密过程,图5b则显示了对图4b中的K节点网格的加密结果。


4 K节点应力集中系数的计算方法
4.1 K节点应力集中系数的定义
管节点在焊缝处的应力分布不均匀,如图6所示。在轴向力作用下,支管在远离加力点和焊缝处截面上的应力分布是均匀的,大小为σn,称为名义应力。在焊缝周围,由于存在着应力集中,应力要比名义应力大得多,这个区域内的应力称为热点应力σh。热点应力和名义应力的比值称为应力集中系数,它反应了主管和支管交线处由于曲率不连续而造成的应力“突变”程度。
按照上述定义,K型管节点的应力集中系数(SCF)可以由以下公式计算得到:


公式(8)中的名义应力可以由下面的公式计算得到:

公式(9)中,d和t分别为支管的直径和厚度。
公式(8)定义了管节点应力集中系数的计算方法。但是,以前的研究工作中对如何计算热点应力一直存在着不同的看法。目前比较普遍采用的对热点应力的定义有两种:第一种是认为热点应力区内某点的热点应力就是该点处的最大主应力;第二种观点认为焊缝处某点的热点应力是垂直于焊缝的法线方向的应力。由于热点应力是用来估算管节点的疲劳寿命的,管节点的疲劳破坏主要是沿着焊缝处表面裂纹的萌生和扩展,因此垂直于焊缝方向的应力应该对裂纹的扩展起主要作用。所以,此处采用第二种规定作为热点应力的定义。
4.2 K节点应力集中系数的试验测试
为了验证有限元方法在计算K型管节点应力集中系数的准确性,测试了两个大型K节点在轴力作用下焊缝周围应力集中系数的分布。两个K节点试件的几何构造如图7a和7b所示。K节点试件由管状空心钢管制作而成,所用的钢管符合API 5L B级规范要求。支管与主管的相交部位采用轮廓线切割技术加工得到,这样可以保证支管和主管在相交部位吻合得很好,已便于焊接。焊接方式采用的穿透焊缝。 K型管节点的中几何参数为:α=43.3(α=2L/D,L为主管长度,D为主管直径),β=0.516(β=d/D,d 为支管直径),τ=0.75(τ=t/T,t为支管厚度,T 为主管厚度)和 γ=5.376(γ=D/2T)。K 节点试件的 γ 取值小于有关规范(如CIDECT)规定的范围,这是为了验证焊缝尺寸对应力集中系数的影响。以往对大型K节点试件的测试也曾有过报道,如Soh和Soh[11]曾对薄壁的K节点的应力集中系数进行过测试。由于管壁很薄,所以γ值很大。在数值模拟时,焊缝尺寸就被忽略了。当γ很小时,焊缝尺寸相对比较大,因而就不能忽略它对管节点应力集中系数的影响。

在进行试验测试的时候,K节点试件主管的两个端部通过螺栓固定在墙体上,可以视为固支边界条件。两个支管中的一个在端部也用螺栓固定在墙体上,在另外一个支管的端部施加轴向力,如图8所示。
在试验测试中,采用应变片测量热点应力区附近的应力。因为应变片有其自身的尺寸要求,所以它不能直接放置在焊趾部位来测量这个部位的应力,而是通常在一个规定的插值区域内布置应变片。在管节点中,用线性外推插值法来确定热点应力。这个插值区距离焊缝有一定的距离限制,其范围可参考有关规范 (如CIDECT)。如图9所示,在规范规定的插值区内可以粘贴两片(线性插值)或者三片(二次插值)应变片。焊缝处的应力可以通过将插值区内的应力外推插值得到。
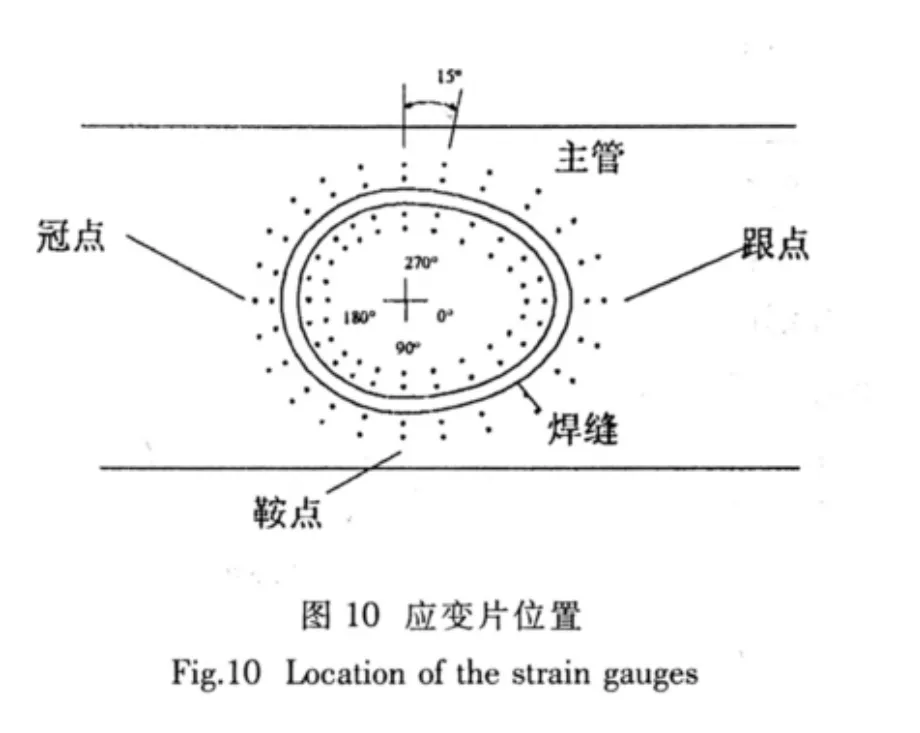
在试验中,支管和主管上在焊缝附近的插值区内每隔15°布置应变片,如图10所示。在每个点上,用两个应变片测量垂直于焊接路径上的应变,两个应变片布置在CIDECT规范所规定的外推插值范围内。试验中在主管上应变片离焊缝的最短距离Lr,min和最远距离Lr,max分别为10mm和18mm,支管上这两个距离分别为8mm和20mm。


4.3 K节点应力集中系数的试验和数值结果
采用提出的有限元模型,可以分析得到承受轴力的K节点试件焊缝处的应力集中系数分布。数值结果的精确程度可以通过和试验测试得到的结果进行比较,以验证有限元模型的适用性。图11a和11b中对两个K节点试件的有限元结果和试验测试结果进行了比较。从图中可以看出,有限元结果和试验结果吻合得比较好,它比较准确地反映了应力集中程度沿着焊缝的分布情况。从图11中也可以发现:对于承受轴力的K节点试件,当管壁厚度相对于直径而言比较大的时候(即γ比较小),主管上沿着焊缝周围的最大应力位于冠点处。支管上沿着焊缝应力变化不是特别明显,它受焊缝尺寸的影响比较明显。

通过对K节点的有限元分析结果和试验测试结果的比较,可以得到如下结论:本文提出的对焊接K节点的几何和数值模拟方法可以比较准确地模拟其热点应力区域内沿着焊缝周围的应力分布情况,因此这种提出的模型可以可靠地用来分析轴力作用下K节点应力集中系数的大小。
5 计算K节点应力集中系数的参数公式
5.1 几何参数对K节点应力集中系数的影响
K节点焊缝周围的应力分布情况是受许多因素影响的,如几何参数、载荷类型、边界条件、焊接质量和初始缺陷等。在本研究中,将不考虑焊接质量和初始缺陷的影响,而且只考虑K节点承受轴向平衡力作用力的作用(如图12所示),所以载荷类型是确定的。在对K节点进行分析时,主管两个端部是固支或简支的,这里采用固支的边界条件。考虑了以上情况后,承受轴力的K节点的应力集中系数就由节点的几何参数决定。国内外对管节点进行分析的时候,都是用几个无量纲的几何参数来表示不同的管节点类型。对于K节点,采用的几何参数有:α(主管长度L/主管半径R)、β(支管半径r/主管半径R)、γ(主管半径R/主管厚度T)、τ(支管厚度t/主管厚度T)和主管与支管之间的夹角θ。在α大于一定的数值的时候,边界条件(固支或者简支)对应力分布基本没有影响,所以,在模型分析中,将α的值固定在15上,从而不需要再考虑α和边界条件的影响。基于以上考虑,在模型分析中,只需要研究几何参数β、γ、τ和θ对K节点在承受轴向力作用下沿着焊缝周围应力集中系数的大小。在模型分析中,如果两个K节点具有相同的几何参数β、γ、τ和θ,则这两个K节点具有相同大小的应力集中系数,而且沿着焊缝周围应力集中系数的分布情况也是相同的。
在K节点的参数分析中,模型是根据四个几何参数(β、γ、τ和θ)的不同而定义的。K节点几何参数范围如下:
· 0.30≤β≤0.60
· 12≤γ≤30
· 0.25≤τ≤0.95
· 30°≤θ≤60°
·两个支管尺寸相同,且与主管有相同大小的夹角
·支管之间有间隙,不考虑交叠K节点。两个支管和主管的轴线交于一点,即无偏心。
在模型的参数分析中,每个几何参数的取值如表1所示。根据表1中所列几何参数的范围和步长,总共分析了1008个K节点模型。


表1 模型分析中几何参数的范围Tab.1 Geometrical range of the analyzed models


根据参数分析的结果,可以总结出K节点在轴向荷载作用下的应力集中系数随着四个几何参数的变化而改变的规律。在研究某个几何参数对K节点应力集中系数的影响时,把其它三个参数的大小固定。γ和β对K节点应力集中系数(SCF)大小的影响如图13a和13b所示。在θ,γ和τ一定的情况下,主管上的应力集中系数随着β的增大而增大,而支管上的应力集中系数却随着β的增大而减小。在θ,β和τ固定的情况下,主管和支管的应力集中系数均随γ的增大而增大。
其它两个几何参数(τ和θ)对K节点应力集中的影响如图14a和14b所示。K节点主管和支管上的应力集中系数均随着τ的增大而增大。同样,主管和支管上的应力集中也都将随着θ的增大而增大。
5.2 计算K节点应力集中系数的参数方程
目前国内关于K型管节点应力集中系数的计算公式尚无报道。国际上比较流行使用的CIDECT规范中对轴力作用下K节点应力集中系数的计算曾提供了一种计算方法。这种方法是把K节点的应力集中系数表示为几何参数的函数,但是需要从有关图中确定应力集中系数的大小。这样在从图中读取数据时必然存在误差。为了简化对K节点应力集中系数的计算方法,这里把K节点应力集中系数表示为如下形式:

指数a和b的变化范围为0到1.1。SCF0是一个关于参数β的方程,SCF0可以由二次多项式的曲线拟合得到。μ是一个修正系数,它是由夹角θ决定。
在拟合用来估算K节点应力集中系数参数公式时,所提出的参数方程必须满足如下要求:在参数适用范围内,所提方程必须能够准确反映各几何参数对应力集中系数的影响规律,且所提参数方程必须简单适用,可以方便地用于工程设计中。方程(10)便是一个典型的可用来计算K型管节点应力集中系数的参数公式。它是基于曲线拟合法得到的,该方程形式满足以上要求。在参数分析中,分别对θ=30°,45°和60°时K节点的应力集中系数进行分析,几何参数对节点SCF的影响都可以反映在方程中。
使用软件DataFit6.0[12]对1008个K节点模型的应力集中系数结果进行了非线性曲线回归分析,得出了离散度在允许范围内的K节点应力集中系数的参数方程,共有六个参数方程,如表2和表3所示。表2为K节点在轴向荷载作用下的支管的应力集中系数参数方程,表3为主管的应力集中系数参数方程。当K节点的主管和支管间夹角θ不等于30°,45°或60°时,其应力集中系数值可以由相同几何参数(β,τ和γ)的K节点在θ为30°,45°或60°时的应力集中系数值通过内部插值法得到。

表2 轴力下K节点支管上应力集中系数的参数方程Tab.2 Parametric equations of SCFs on the brace for K-joint under axial loads

表3 轴力下K节点主管上应力集中系数的参数方程Tab.3 Parametric equations of SCFs on the chord for K-joint under axial loads
5.3 K节点应力集中系数参数方程精确性的验证
拟合得到的用于计算K节点应力集中系数的参数方程需要验证其精确性。表2和表3所列的参数方程是基于对1008个K节点模型结果的基础上。这1008个节点模型的几何范围可以从表1中得到。如果所提出的K节点应力集中系数的参数方程的精确性得到验证,那么它可以用来比较精确地计算表1所规定几何范围内的任何一个K节点的应力集中系数。
在验证提出的参数公式的精确性时,可以通过将从参数公式计算得到的结果与有限元计算得到的结果进行比较,观察其相对误差的大小。相对误差Er可以通过下式表示:

其中,SCFE是由参数方程得到的K节点应力集中系数值,SCFN是有限元分析计算得到的K节点应力集中系数值。
对参数分析中的1008个K节点模型的应力集中系数值的相对误差按照公式(11)进行计算,所得到的结果如图15所示。图15中,横坐标N表示模型个数。从图15中很容易看出:对于1008个K节点模型,由参数公式计算得到的K节点应力集中系数的大小和有限元结果比较,其相对误差绝大多数都在±20%以内。所以,所提出的参数方程在计算轴力作用下K节点应力集中系数大小方面是精确可靠的。

6 结 论
本文提出了对K型管节点的几何和数值模拟,尤其是对焊缝的模拟。通过对两个大型K节点模型的试验测试,验证了所提出的有限元模型在计算轴力作用下K节点沿着焊缝处的应力集中系数时是准确可靠的。在此基础上,通过对1008个K节点模型的参数分析,研究了几何参数对K节点应力集中系数的影响。最后通过曲线拟合提出了K节点在轴向力作用下支管和主管上应力集中系数的参数方程。通过将参数方程计算所得的应力集中系数的结果与有限元分析得到的应力集中系数的结果来进行比较,发现所提出的参数方程具有相当的精确度,从而可以安全可靠地用于工程设计中。
[1]Zhao X L,Herion S,Packer J A,Puthli R,Sedlacek G,Wardenier J,Weynand K,van Wingerde A,Yeomans N.Design guide for circular and rectangular hollow section joints under fatigue loading[K],CIDECT,TUV,2000.
[2]陈铁云.近海钻井平台管状接头应力分析的进展[J].力学进展,1985,4(25):425-433.
[3]陈伯真.海洋平台管节点应力分析研究工作展望[J].力学进展,1987,17(3):331-336.
[4]李华明.海洋平台管节点的热点应力测量[J].振动、测试与诊断,1991,11(3):23-29.
[5]陈铁云,朱正宏.海洋平台T、Y、K及塔接K型管接头的弹塑性有限元分析[J].海洋工程,1992,10(2):8-15.
[6]王春光,李少甫,石永久.焊接钢管节点热点应力集中系数参数方程的适用性研究[J].工程力学,1999,16(6):44-53.
[7]Cao J,Yang G,Packer J A.FE mesh generation for circular joints with or without cracks[C]//In:Proceedings of the 7th International Offshore and Polar Engineering Conference.USA,1997,IV:98-105.
[8]American Welding Society.Structural welding code-steel[S].ANSI/AWS,D1.1-2000.Miami,USA,2000.
[9]Lee M M K,Bowness D.Prediction of stress intensity factors in semi-elliptical weld toe cracks in offshore tubular joints[C]//Proceedings of the 9th International Symposium and Euroconference on Tubular Structures.Dusseldorf,Germany,2001:299-308.
[10]Herion S,Mang F,Puthli R.Parametric study on multiplanar K-joints with gap made of circular hollow sections by means of the finite element method[C]//In:Proceedings of the 6th International Offshore and Polar Engineering Conference.Los Angeles,USA,1996,IV:68-73.
[11]Soh A K,Soh C K.Stress concentrations of K-tubular joints subjected to basic and combined loadings[C].Proceedings of the Institute of Civil Engineering-Structures and Buildings,1996,116:19-28.
[12]DataFit 6.0.Oakdale Engineering[DB].23 Tomey Road,Oakdale,Pa,USA,1998.
