低频信号注入法的永磁同步电机无速度传感器控制

徐艳平,郜亚秋,钟彦儒

（西安理工大学自动化与信息工程学院，陕西西安710048）

1 引言

永磁同步电机具有效率高、功率因数高、转动惯量小等特点，因此在高性能、高精度伺服领域得到越来越广泛的应用。通常永磁同步电机的控制系统中需要在转子轴上安装机械传感器用来测量转子的位置和速度，但是机械传感器的安装会带来很多问题，例如，加大安装尺寸，增加系统成本，维护困难等等。因此，无速度传感器控制技术已经成为研究的热点问题［1]。已有的永磁同步电机的无速度传感器矢量控制中通常采用反电动势来估计转速，但是电机在低速时的反电动势很小，无法获得较好的控制效果。

低频信号注入法是在矢量控制基础上，通过注入的电流信号产生的电压响应来获得估计的转速和转子位置信息［2] -［5]。本文首先叙述了低频信号注入法的永磁同步电机无速度传感器的控制原理，在此基础上针对一台永磁同步电机进行了仿真，仿真结果验证了低频信号注入法的正确性和有效性。

2 低频信号注入法的转速估计原理

矢量控制利用的是解耦思想，在同步旋转d-q坐标系下通过控制电流在d-q轴上的分量id和iq的幅值和相位实现对电机的控制。低频信号注入法采用在电机的d轴注入一定频率的低频电流信号，通过检测由注入的信号产生的电压响应，经过信号处理来获取转速和转子位置信息。

假设d-q坐标系的d轴与永磁同步电机的磁场方向一致，可得到永磁同步电机在d-q坐标系下的数学模型为：

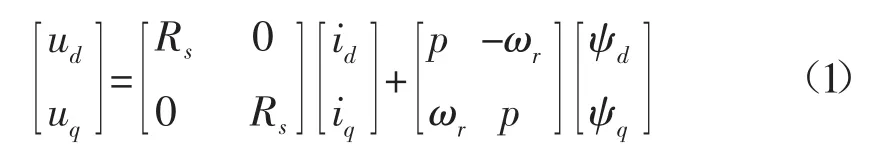
式中：ud、uq、id、iq、ψd、ψq分别为定子电压、定子电流、定子磁链的d轴和q轴分量；Rs为定子电阻；ωr为转子电角速度；p为微分算子。

定子磁链可以表示为：

式中：Ld、Lq分别为d轴和q轴电感；ψm为转子永磁磁链。

由于表面式永磁同步电机的d轴和q轴的电感相等，用L代替Ld、Lq并将式（1）代入式（2）可以得到：

将q轴反电势定义为：

电磁转矩为：

式中：np为极对数。

系统的运动方程为：

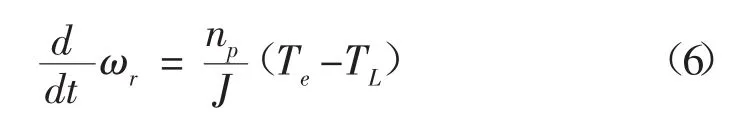
式中：J为转动惯量,TL为负载转矩。

由icq引起的电磁转矩响应为：

将式（4）代入系统运动方程并假定负载转矩恒定，得到谐波引起的转速响应为：

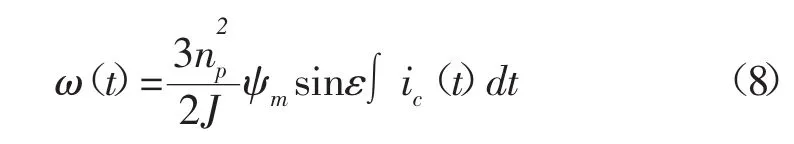
根据式（4）和（8），可以得到注入信号引起的q轴反电势响应为：

该响应在估计的q轴上的分量为：

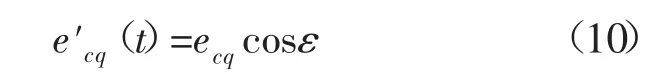
假设误差角ε足够的小，可得：

通过上面的推导可以得到，如果控制e′cq为零，就可以准确估计转子位置。通过控制e′cq就可以控制ε为零。由于无法直接得到误差ε,需要构造一个误差函数 Fε,使得当 Fε＝0 时，ε＝0。得到的构造函数为：

经过PI调节，得到的转速估计值为：

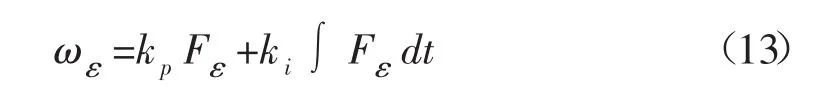
理论上，由式（13）即可得到转速估计值，但是为了提高系统的动态响应速度，由式（3）得到转速的稳态值为：

式（14）与由误差信号得到的转速估计值相叠加，得到最终的转速估计值为：

因此通过上述可以得出转子位置角为：

上述即为低频信号注入法永磁同步电机转速估计的基本原理，低频信号注入法的永磁同步电机无速度传感器矢量控制系统的原理如图1所示，图1中PMSM采用id＝0控制策略，速度调节器输出电流指令值。电流检测单元获取电机定子三相绕组的瞬时相电流，然后对相电流进行坐标变换，计算出电流空间矢量在d轴和q轴上的等效电流分量id、iq。把id、iq和电流给定值idref、iqref的差值分别送给电流调节器，电流调节器输出空间电压矢量在d轴和q轴上的等效电压分量udref和uqref，经过坐标变换后送给电压空间矢量脉宽调制（SVPWM）波形发生器，控制逆变器的开关状态。

图1 低频信号注入法的PMSM矢量控制系统框图

3 仿真分析

为了验证采用低频信号注入法估计永磁同步电机转速的正确性和有效性，利用Matlab/Simulink软件对低频信号注入法进行了仿真。仿真中永磁同步电机的参数为：定子电阻Rs＝0.2Ω，直轴和交轴电感为 Ld＝Lq＝8.5mH，转子永磁磁链 ψm＝0.24Wb，转动惯量J=1.2e-3kg·m2，极对数np=4。得到的仿真结果如图2-图5所示。

在低频信号注入法中，注入的低频信号的频率和幅值是影响该估计方法性能的重要因素。为了确定适当的注入信号的频率和幅值，分别进行了确定频率变化幅值和确定幅值变化频率的仿真，所取得的仿真结果如图2、3所示。

图2 注入信号f 为66.5Hz 时不同幅值对应的转速

图2是注入信号频率为66.5Hz，幅值分别为2.0A、1.5A、1.0A 下的实际转速与估计转速的仿真波形。从图2中可以看出，当注入信号的频率为66.5Hz时，幅值在一定的范围内估计转速都可以准确地跟踪实际转速的变化，但是随着幅值的增加，转速稳态时的波动值的范围会有所增加，因此，选取的注入信号的幅值不宜过大；同时注入低频信号的幅值在减小的过程中，动态调节部分的作用会逐渐减弱，使得获得转速估计值有所下降，因此幅值选取也不能过小。基于以上原因本系统中选用的低频注入信号的幅值为1.5A。

图3 注入信号幅值1.5A不同频率对应的转速

图3是注入信号的幅值为1.5A，频率分别为40Hz、66.5Hz、80Hz下的实际转速与估计转速的仿真波形。从图3中可以看出，注入信号的幅值为1.5A时频率在一定的范围内都可以实现对电机实际转速的准确估计；同时随着频率的增加，转速稳态时的波动值的范围会有所减小。本系统中选用的低频注入信号的频率为电机的额定频率的二分之一66.5Hz。

图4是给定转速为0rad/s情况下的实际转速、估计转速和转矩的仿真结果，从图4中可以看出，给定转速为0rad/s时系统可以稳定运行，估计转速与实际转速趋势一致，并且当转矩在0.5s时从0突増至7.15N·m时，系统经过短暂的调节后仍然可以稳定运行。

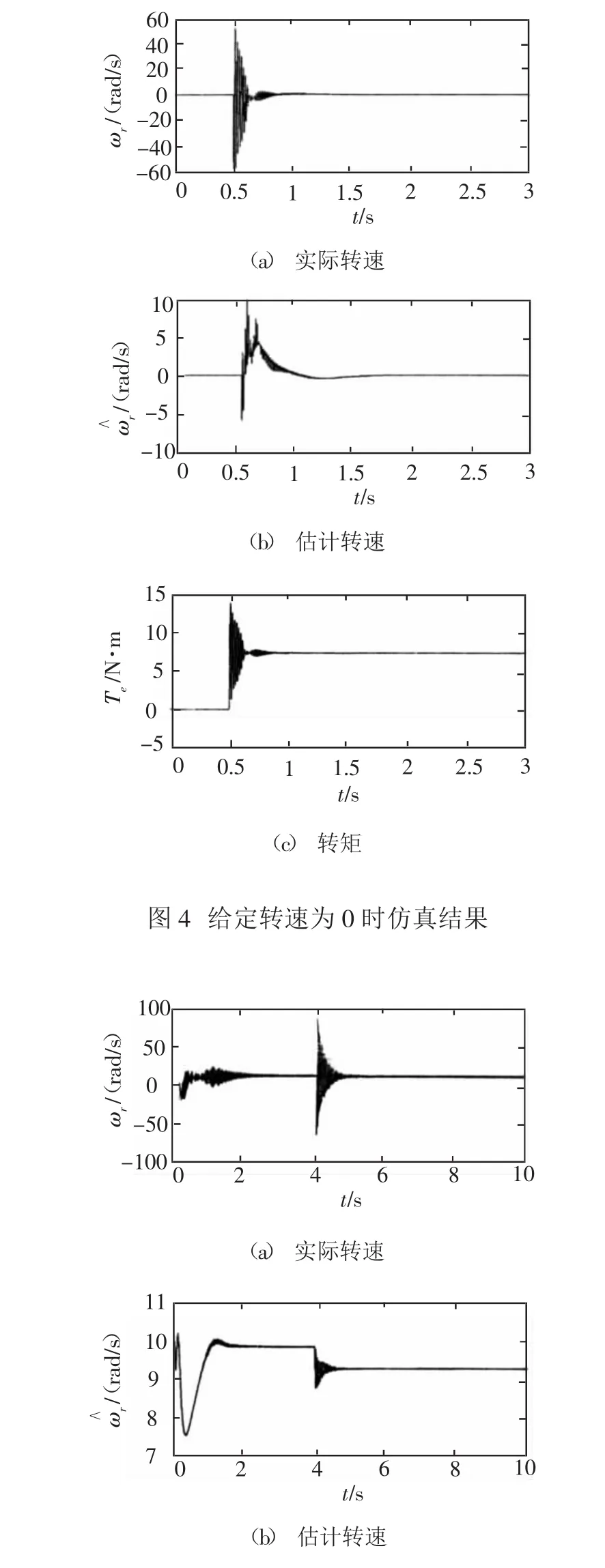
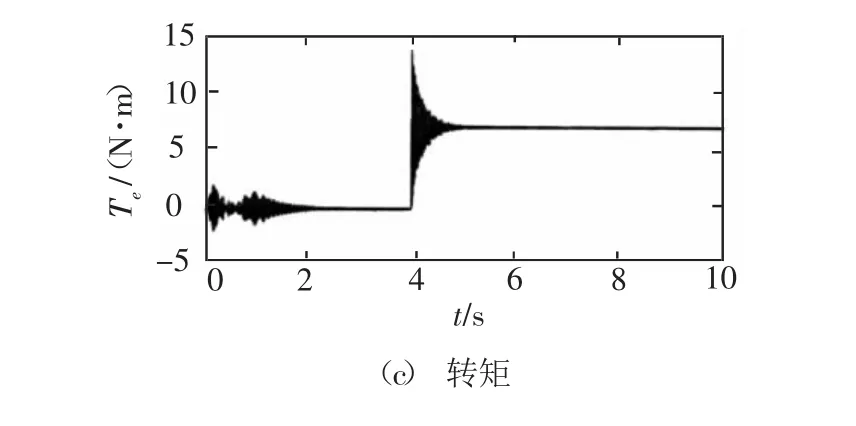
图5 给定转速为10rad/s时的仿真结果

图5是给定转速为10rad/s情况下的实际转速、估计转速和转矩的仿真结果。可以看出系统可以稳定运行，虽然转速在起动阶段存在震荡，但在很短的时间内可以消除，估计转速可以跟踪实际转速，同时，当转矩在4s时突増至7.15N·m时，估计转速经过波动后，仍可以较快地估计出实际转速并输出恒定的转矩。体现出了较好的鲁棒性。

4 结论

本文针对永磁同步电机矢量控制，采用低频信号注入法来实现电机的无速度传感器控制，仿真结果证明了这种方法在电机低速及零速时都可以准确地估计出电机真实转速。由于这种方法是基于电机的基波模型而且不依赖于电机的凸极效应，具有控制简单、鲁棒性好并且适用广泛的特点，是一种适合于永磁同步电机低速段甚至零速下的转速估计方法。

［1] 李永东.交流电机数字控制系统[M].北京：机械工业出版社，2002.

［2] 吴姗姗，李永东.基于信号注入的极低速PMSM无速度传感器控制［J] .电气传动，2008，38（1）：19-22.

［3] Kereszty T,Leppanen V M,Luomi J.Sensorless control of surface magnet synchronous motors at low speeds using low-frequency signal injection ［J] .IECON,2003:1239-1243.

［4] Matti Eskola,Heikki Tuusa.Sensorless control of salient pole PMSM using at low-frequency signal injection［J] .EPE，2005:1-10.

［5] ShanshanWu,Yongdong Li,Xuejin Miao.Two signal injection methods for sensorless control of PMSM at very low speeds［J] .IEEE PESC 2007:568-573.