轴流压缩机的扩压因子流型非等功设计方法及其应用

杨元英, 谷传纲

(上海交通大学动力与机械工程学院,上海200240)

轴流式叶轮机械设计仍然广泛采用径向或沿子午流线准正交方向平衡计算方法.在前后排叶片间隙间,这些设计方法都存在一个设计自由度,其沿径向的分布规律就确定了叶片的成型,称这种分布规律为“扭转规律”或“流型”,如等环量、等出口角等.但不等功设计方法在轴流式叶轮机械设计中使用更普遍,它是指欧拉功沿径向不相等的叶片设计方法,可以克服在等功设计中经常遇到的叶片根部弯曲严重导致提前失速的缺点.

笔者直接把“扩压因子”作为一个设计度,因为扩压因子不仅表征负荷的大小,还可以通过经验公式表示损失的大小,并且与基元叶片的负荷极限有大量的试验数据关联可供使用,是表征压气机性能最适宜的参数之一[1].对扩压因子流型的掌握可以使设计者处于主动地位,充分发挥叶片的做功能力,扩大变工况范围,因此本文采用扩压因子的分布作为规定“流型”的参数,应用非等熵完全径向平衡方法编制计算机程序.为了验证程序的正确性和可行性,还使用该程序设计了一个轴流风机,然后利用Numeca/Fine软件对轴流风机进行模拟计算,并对模拟计算结果和程序计算结果进行比较分析.最后对扩压因子流型的应用进行分析.

1 扩压因子流型的设计方法

在图1中2-2截面和3-3截面处分别选取动叶扩压因子和静叶扩压因子作为设计参数,采用无叶间隙处非等熵完全径向平衡计算方法来求解径向平衡方程.在计算中,假设流动非等熵、相对定常、轴对称;仅考虑粘性历史积累的影响,忽略当地粘性力的作用;叶型损失、端部损失和二次流损失等均采用熵增来估算[2-3].

图1 子午流道示意图Fig.1 Schem atic diagram ofmeridian path

1.1 基本方程

基本方程包括连续性方程、径向运动方程、能量方程、理想气体状态方程以及转子和静子的扩压因子表达式.

连续性方程：

式中：Cr为绝对速度的径向分量;Cz为绝对速度的轴向分量.

径向运动方程：

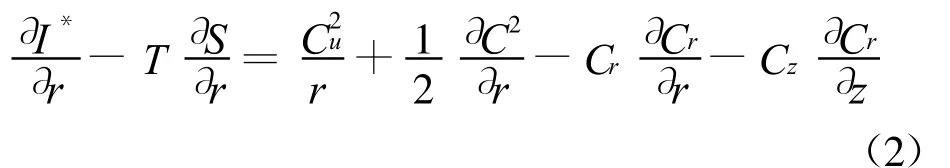
能量方程：

式中：I*为总焓;L为欧拉功;Cu为绝对速度的周向分量;C1u和C2u分别为动叶前、后绝对速度的周向分量;S为流体沿流线的熵;U为旋转速度;下标1、2分别表示变量为1-1截面和2-2截面的变量.

理想气体状态方程：

式中：p为气体压力;T为气体温度;ρ为气体密度;R为气体常数.

转子的扩压因子表达式：

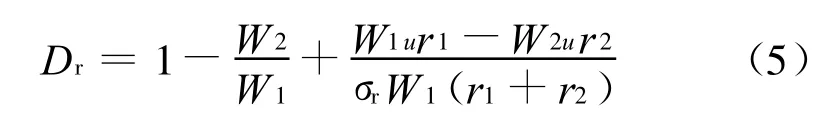
式中：W 1和W 2分别为动叶前和动叶后的相对速度;W1u和W 2u分别为动叶前和动叶后相对速度的周向分量;σr为动叶叶栅稠度;r1和r2分别为同一条流线动叶前和动叶后的半径.

静子的扩压因子表达式：

式中：C2和C3分别为静叶前和静叶后的绝对速度;C2u和C3u分别为静叶前和静叶后绝对速度的周向分量;σs为静叶叶栅稠度;r3为静叶后的半径.

1.2 计算公式

1.2.1 基本计算公式

引入等环面积曲线坐标对基本方程(1)～(4)进行化简,得到各截面的计算公式如下：

式中：fj请参考文献[4];Ψ为子午流线方向与轴向夹角;Cm为子午面速度;表征曲率影响;j=1,2,3分别表示3个截面.

经分析可知,每一截面均有并且只有一个设计自由度,这个设计自由度(即流型)可以是给定Cu(rj)、β(rj)、D(rj)、H(rj)和 p(rj)等.

流量方程为：

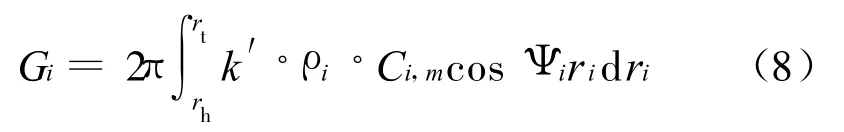
式中：k′为考虑附面层的流量修正系数;r t、r h分别为上、下边界的半径.

1.2.2 子午流道各截面的计算

对于图1中1-1截面,一般认为其熵和总焓为常数,给定：

式中：A1、B1均为待定参数.

将式(9)代入式(7),整理后得：

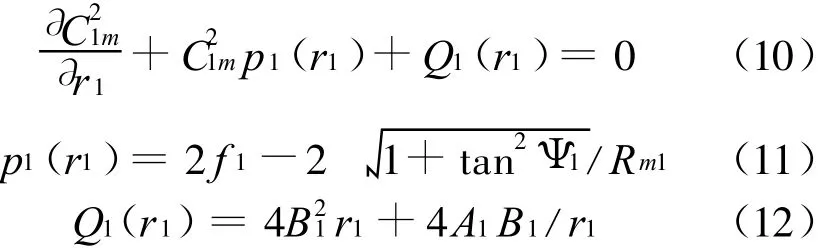
图1中2-2截面和3-3截面都是给定扩压因子分布,其求解方法相同.下面以2-2截面为例,说明求解计算方程的具体方法.首先将式(7)中所有非独立的未知量都化为C2u的函数,经整理后得到一个未知变量C2u r2的一阶非线性常微分方程：

式中 ：a1、a2、a3、a4 请参考文献[4].

根据Dr的分布,用变步长 Runge-Kutta法(四阶六级计算公式)求解方程(13),由于其中∂S2/∂r2项的数值必须根据本截面的C2u和β2值,可用损失经验公式和熵增具体公式求得.所以,在计算中采用β2迭代和隐式求解.采用隐式求解可以提高解的稳定性和收敛性.此外,也可从第2次迭代开始直接采用上一次计算值作为本次的初始值,进行迭代.

2 设计实例与模拟计算

为了验证程序的有用性和可行性,利用程序设计了1个由转子和后导叶组成的轴流式风机,然后采用商业软件Numeca/Fine对轴流风机进行了模拟计算,并将设计结果与模拟计算结果进行了比较.

2.1 设计参数

风机的设计参数为：叶顶直径900 mm;轮毂直径290mm;设计流量31 000m3/h;转子和静子的叶片数均为7.动叶采用等绝对出口气流角,α2取19.5°,静叶采用轴向出气,α3取 0°.给定 C1u(r1)的分布为：C1u(r1)=5r1-0.5/r1,D r(r2)和D s(r3)的分布见图2.风机的动叶和后导叶叶片形状见图3,叶片原始叶型采用NACA65-010,中弧线为单圆弧.

图2 动叶后和后导叶后截面扩压因子的分布Fig.2 Distribution of diffusion factor after rotor and back guide vane

2.2 模拟计算

采用Numeca/Fine软件对风机进行了模拟计算.风机流道网格利用AutoGrid5生成,动叶和后导叶都仅取单通道.动叶径向、轴向和周向网格点数分别为113、139和59.后导叶径向、轴向和周向网格点数分别为113、127和59.动叶和后导叶总的网格数为2 495 992.在计算时,采用S-A湍流模型,壁面网格满足y+max＜10.

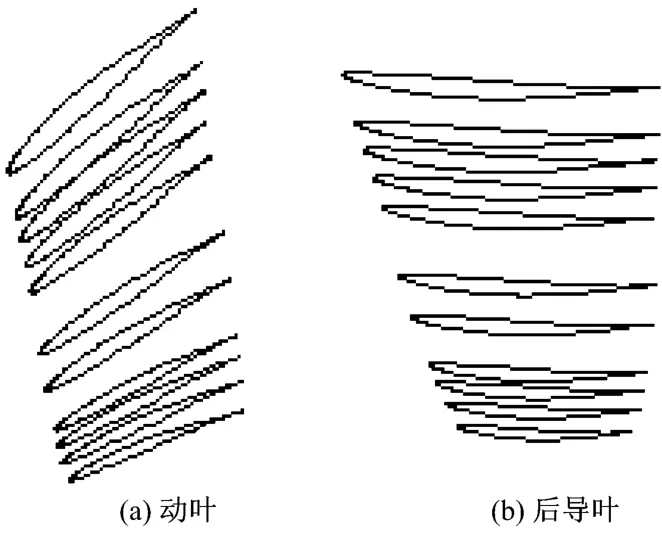
图3 动叶和后导叶Fig.3 Rotor and back guide vane

边界条件(1-1截面)如下：①进口给定总压为102 370 Pa,总温为295 K和轴向进气;②出口给定质量流量为 10.98 kg/s;③转、静子界面为混合界面.

3 设计结果与模拟计算结果的比较

为了便于比较,对图1中3个截面上的参数分布进行了分析.图4～图7给出了利用程序得到的设计结果与采用Numeca/Fine软件得到的模拟结果的比较.

图4 第一个截面的子午面速度比较Fig.4 Com parison ofm eridian velocity on first section

图5 第二个截面的周向速度比较Fig.5 Comparison of tangential velocity on second section

图6 第二个截面的子午面速度比较Fig.6 Comparison of meridian velocity on second section

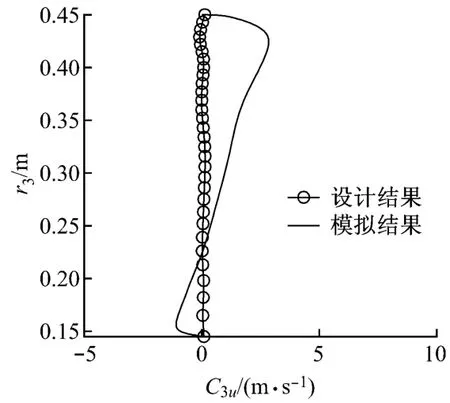
图7 第三个截面的周向速度比较Fig.7 Com parison of tangential velocity on third section

由图4～图7可以看出,程序设计结果与模拟计算结果除在两端部差别较大外,中间部分吻合较好.偏差产生的原因可能是两个程序求解方法不同以及所选用的损失模型本身具有误差,其中端部偏差较大可能是由于diffusion程序没有充分考虑端部的摩擦损失.由于diffusion程序没有采用顶部泄漏损失模型,故在Numeca/Fine模拟计算时径向间隙设为0.0mm.从图4～图7还可以看出,2-2截面的设计结果与模拟计算结果非常吻合,而3-3截面有较大偏差,这可能是由于转、静子界面为混合界面导致后导叶入口参数变化较大造成的.同时,模拟计算得到的风机绝热等熵效率为82.1%,而设计程序计算得到的风机绝热等熵效率约为86%,表明设计程序中使用总压损失计算公式得到的损失,相对于Numeca/Fine数值模拟计算得到的损失有点偏小,今后可通过试验结果加以修正.

4 扩压因子流型的一些应用规律

扩压因子流型以扩压因子作为设计参数,根据设计要求可以给出一个比较合理的扩压因子分布,对于初步设计,可以假设动叶扩压因子的分布如图8所示,其中阴影部分为取值范围.由文献[5-6]测得的试验值表明,动叶顶部流动情况复杂,变工况畸变严重,故顶部扩压因子应取小于0.4,动叶根部由于圆周速度低,做功能力小,若要使出口总压尽量均匀,则应使根部扩压因子大一点.根据试验,如果要使喘振裕度不小于15%,则应使D cp(设计扩压因子平均值)不大于0.5,故根部的扩压因子应尽量小于0.5,以避免根部提前失速.

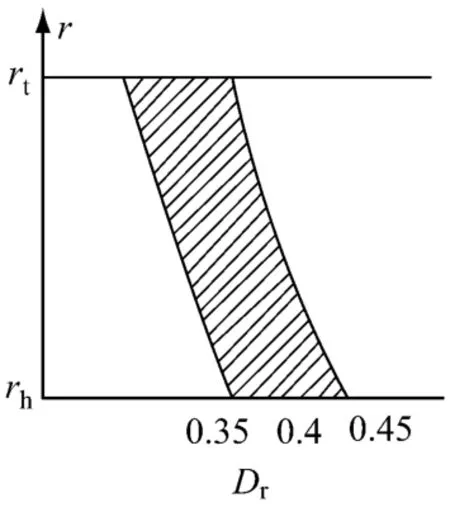
图8 动叶扩压因子的分布Fig.8 Distribution of diffusion factor of rotor

虽然NASA大量的资料表明,静叶扩压因子基本上呈“C”型分布,但从保证出口静压均匀(减少掺混损失)和提高变工况范围出发,“C”型扩压因子分布易使静子轮毂处负荷偏大,从而导致提前失速.根据经验,通常在动叶顶部反动度较小且加工量大,导致顶部绝对速度大,为了满足级出口要求和改善后续级的进口条件,在顶部可以采用较大的扩压因子,但应小于0.6.根部出口速度本来就小,其扩压因子应小于0.4,否则可能引起分离,建议采用图9所示的静叶扩压因子分布,其中阴影部分为取值范围.

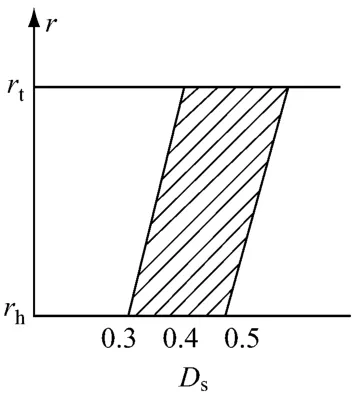
图9 静叶扩压因子的分布Fig.9 Distribution of diffusion factor of stator

5 结 论

(1)扩压因子流型采用非等熵完全径向平衡计算方法的结果表明：该方法简单明了,具有一定的精度和实用意义.

(2)扩压因子流型作为一种非等功设计方法,其主要优点是可以通过直接控制叶片负荷、负荷极限和喘振裕度等指标来进行叶片设计.当然,对于扩压因子流型的更合理分布以及最优流型命题[1,7],仍有待进一步研究.

[1] 谷传纲.轴流压缩机最佳流型的理论研究[J].上海机械学院院报,1982,4(3)：45-61.GU Chuangang.Theory of op timal flow-type of axialflow compressor[J].Journal School of Shanghai Mechanical Engineering,1982,4(3)：45-61.

[2] GU Chuangang,M IAO Yongm iao.Blade design of axial-flow comp ressors by the method of op timalcontrol theory-application and results[J].ASME Journal of Turbomachinery,1987,109(1)：102-108.

[3] GU Chuangang.New development of turbo-comp ressor and fan on design,re-rating and numerical simulation in China[C]//Proceedings o f the KFMA Annual Meeting 2000.Pusan：Korea Fluid M achinary Association,2000：1-7.

[4] 杨元英.轴流式压缩机的扩压因子流型不等功设计方法及其应用[D].上海：上海交通大学动力与机械工程学院,2010：12-23.

[5] JOHNSEN I A,BOLLOCK R O.Aerodynam ic Design of Axial-flow Comp ressor[M].Washington：NASA,1965.

[6] 康婷,李雪松,顾春伟.微型燃气轮机向心透平内部流动分析[J].热力透平,2009,38(2)：78-81.KANG Ting,LI Xuesong,GU Chunwei.Flow characteristics of the radial in flow turbine rotor of a micro gas turbine[J].Thermal Turbine,2009,38(2)：78-81.

[7] 高闯,谷传纲,王彤,等.基于模糊理论的三维无叶扩压器多目标优化[J].上海交通大学学报,2006,30(7)：1192-1196.GAO Chuang,GU Chuangang,W ANG Tong,et a l.The multi-criteria optimization o f 3D vaneless diffuser based on fuzzy theory[J].Journal of Shanghai Jiao Tong University,2006,30(7)：1192-1196.