密封间隙内气体流动对气缸动力特性影响的试验研究

孙 健, 孙 丹, 杨建刚, 曹 浩

(东南大学火电机组振动国家工程研究中心,南京210096)

符号说明：

A——振幅峰值,m

c——阻尼系数,kg/s

f——作用力,N

F——激励力频域信号

H——传递函数

k——刚度系数,kg/s2

m——质量,kg

s——拉普拉斯变换因子

t——时间,s

x——振动幅值,m

X——振动频域响应

ω——频率,H z

ωn——共振频率,Hz

ζ——阻尼比

φ——相位角

δ——对数衰减率

随着发电机组向超临界和超超临界快速发展,机组参数逐渐升高,密封腔内的气流力也在逐步增大.在高速旋转轴的驱动下,气流在密封间隙内呈螺旋形流动,导致密封腔内压力分布不均匀,从而产生气流激振力,诱发转子失稳,影响机组安全运行.因此,对密封腔内气流力的研究日益重要.

目前,国内外对密封间隙内气流力的研究主要有密封流场建模仿真计算和试验2种方法.密封间隙内气流为三维可压缩非定常湍流,其流动复杂,仿真建模计算的工作量很大,但试验研究的结果却比较准确.BH Ertas在密封试验台上于不同参数环境下进行了新型密封测试,对密封动力特性系数及泄漏量进行了研究,并与普通密封进行了对比[1].蒋浦宁在气流激振试验基础上,将试验结果与理论计算结果进行了对比分析,研究了密封气流激振力对转子临界转速及稳定性等特性的影响[2].袁振伟等建立了考虑A lford力的系统运动方程,导出了系统模态阻尼、频率及振幅对数衰减率等参数的解析式,并分析了该气流力对系统动力学性能的影响[3].王炜哲等以偏心涡动的转子轴封为研究对象,合理简化了轴封流场方程,并分析了轴封气流周向剪切力对转子动态特性的影响[4].韦康等人构建了各种激振源对转子临界转速影响的计算模型,并且利用该模型就气隙激振力对转子临界转速的影响进行了计算分析[5].

本文在密封试验台上通过试验方法,分析了密封间隙内气体流动对气缸动力特性的影响.

1 密封试验台

图1为密封试验台示意图.本试验台通过电动机和变速齿轮箱带动转轴旋转,转速可在0～6 000 r/m in进行调节.从空气压缩机出来的压缩空气通过供气管路向气缸内部供气,从气缸端部或中间进气,进气方式为部分进气或四周进气.在通气管道上安装流量计和压力表,用于测量气缸进、出口气流的参数.在气缸内壁设计可安装气封的套筒,用于装配不同气封以进行测试.本文设计了气缸支撑系统,以保证气缸内壁无碰撞摩擦,并能调整气缸位置,从而改变密封间隙比.在气缸两端的水平和垂直方向上均布置了速度和涡流传感器,用于测量气缸两端相对振动和绝对振动.在气缸周向上装配了压力传感器,用于测量气流压力沿气缸周向的分布.在轴承端也分别装有传感器,用于测量转轴轴振和轴承座瓦振.在转轴上装有动平衡盘,可根据振动测量结果在动平衡盘不同角度进行动平衡加重,用于调整转轴振动.此外,还设计了润滑油系统,由油泵带动润滑油循环,以减少轴承轴颈间的摩擦,并保证轴承的承载能力.

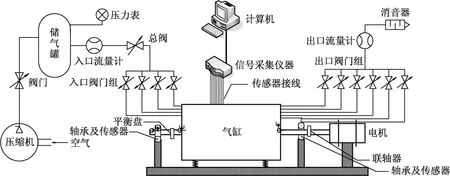
图1 密封试验台示意图Fig.1 Schem atic of the seal test rig

2 气体流动阻尼特性的识别方法

2.1 气缸传递函数

气缸传递函数反映了系统输入输出之间的关系和系统的固有特性,是系统在频域中的一个重要特征量,也是频域内模态识别的依据.将气缸简化为单自由度系统,则系统动态特性可由运动微分方程来描述：

对式(1)两边进行拉普拉斯变换得：

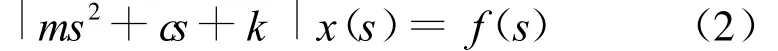
则系统传递函数为：

令 s=jω,得 ：

则该系统的频率响应函数H(ω)为：

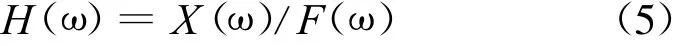
通过测试和分析气缸传递函数及其频率响应可辨识系统的模态,从而获得气缸的共振频率和阻尼等动力特性.

2.2 阻尼系数的计算

常见的测量阻尼系数的方法为半功率带宽法和对数衰减率法.半功率带宽法是一种在频域内求解阻尼系数的方法.该方法通过激励响应测试气缸传递函数,找出其频率响应函数幅值谱半功率点,即取峰值处的两频率点(频率差为Δω),则阻尼系数ζ为：

对数衰减率法是最常见的时域方法,该方法通过响应曲线求取阻尼系数.气缸单自由度系统有阻尼的自由响应公式为：

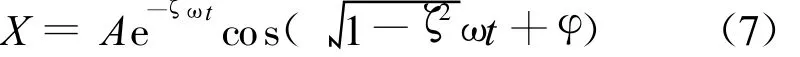
根据响应曲线,取多点峰值进行比较,计算对数衰减率δ,并求取阻尼系数 ζ：

式中：Ai、Aj分别为响应曲线的第i和第j个峰值.

3 试验信号采集与分析

3.1 信号采集与分析

使用虚拟仪器软件LabW indow s/CVI编制数据采集程序来采集试验信号.硬件部分主要采用PMD 1608 FS多功能数据采集卡,该卡使用 USB 2.0接口,有8路独立A/D通道、16位模拟量输入.当采用多通道连续采集模式时,单通道最大连续采样率为 100 000 Hz,双通道最大连续采样率为50 000 H z,以此类推.当采用触发模式工作时,8通道均能够以50 000 H z采样速率同步进行试验信号采集.

在试验时,设置采集程序为连续采样,采样频率为10 000 H z,每次采集10 s内的数据.在不同充气压力和转速下,使用力锤(CL-YD-305A)和配电荷放大器(YE 5852A)在试验台气缸水平与垂直位置上施加激励.试验转速范围为0～2 200 r/min,充气压力为0～0.5 MPa.

图2为力锤激励信号与气缸响应信号曲线图.从图2可知：由于电机干扰、气动噪声、试验台碰撞摩擦及不平衡等原因,采集到的原始数据中含有丰富的宽频噪声.为除去此类噪声,可采用设计数字滤波器或谐波去除的方法进行滤波.在数字滤波器中,通带和阻带间的截止不理想,对于宽频带噪声滤波不完全,通带一般有波纹,并对滤波幅值产生波动.

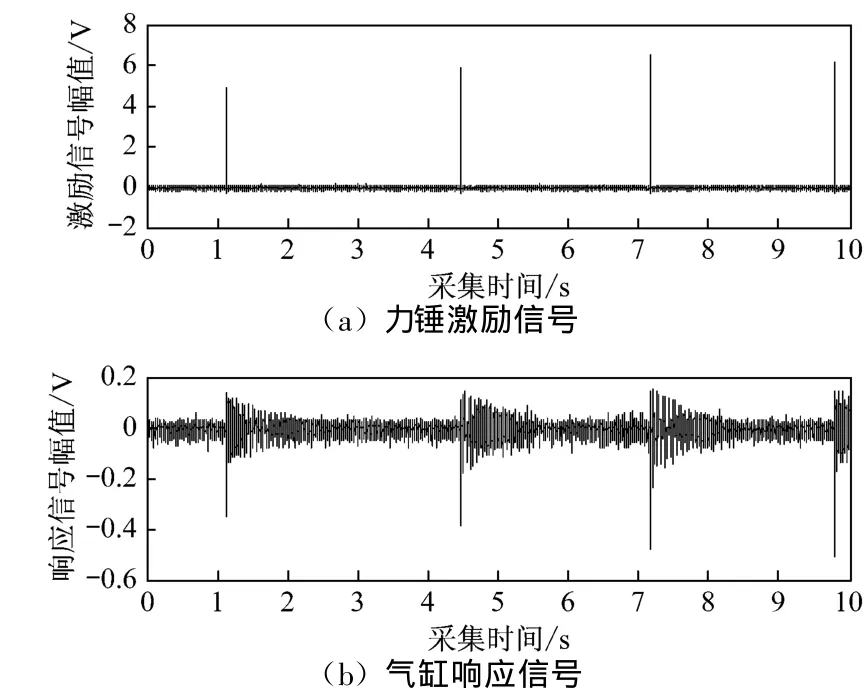
图2 力锤激励信号与气缸响应信号曲线(转速为0)Fig.2 Hammer force signaland the cylinder response curves(0 r/m in)

笔者采用谐波去除法进行滤波.谐波去除法是在频域内对噪声频率成分进行抑制,然后采用反傅里叶变换将频域数据转换为时域数据,时域数据的实部就是滤波后的信号.该方法可获得锐截止的频域特性.根据响应曲线频谱,选择通带截止频率为30 Hz.由于信号长度为 100 000点,采样频率为10 000 Hz,所以保留第 1～300点和第99 700～100 000点频域数据,其他频域数据全部为零.图3为气缸响应原始信号与滤波后信号的对比.从图3可知：滤波后得到了比较满意的时域波形.

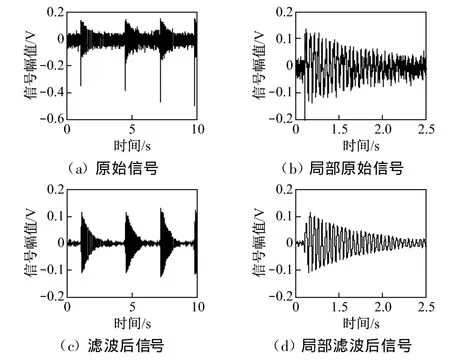
图3 气缸响应原始信号与滤波后信号的对比Fig.3 Com parison betw een the original cy linder response signaland the filtered signal

3.2 频域响应函数的测试

根据试验采集的力锤激励力输入信号F和该力激励下的气缸响应信号X,可以测试系统的频域响应函数.

将力信号和响应信号分别进行频域变换,得到离散的频域函数 F(ω)和 X(ω).根据式(5),将对应的频率点数据相除,即可以求出系统的频域响应函数 H(ω).

4 密封泄漏率的测试

在不同进气压力和转速下,进行了密封泄漏率测试.图4和图5分别为疏齿密封泄漏率随进气压力和转速变化的曲线.从图4和图5可知：密封泄漏率随着进气压力的升高而增加,但转速对密封泄漏率影响不大.

图4 疏齿密封泄漏率随进气压力变化的曲线Fig.4 Variation cu rve of the seal leakage ratesof the labyrin th fin vs.inlet pressu re

图5 疏齿密封泄漏率随转速变化的曲线Fig.5 Variation cu rve of the seal leakage ratesof the labyrin th fin vs.rotation speed

5 密封间隙内气体流动对气缸动力特性的影响

5.1 对阻尼特性的影响

由于采用半功率带宽法计算出的阻尼分散度较高,在小阻尼情况下,即使低频段峰值和频率的误差很小,该方法计算出的阻尼误差也很大.经滤波处理后,气缸响应信号的波形比较理想,所以本试验以对数衰减率法计算出的阻尼结果为准.

图6和图7分别为气缸阻尼系数随转速和压力变化的趋势.从图6可看出：气缸水平方向和垂直方向的阻尼系数均随转速的增加而减小.这是因为转速增加时,转轴摩擦带动气流周向旋转加剧,在密封泄漏率几乎不变的情况下,气缸受到的气流切向激励力增大,使得系统更容易失稳,气缸的阻尼系数减小.从图7可知：随着进气压力的增加,密封间隙气流导致气缸水平阻尼系数和垂直阻尼系数均增大.这是因为进气压力的增加导致密封泄漏率增加,气流与动静部件的摩擦作用更显著,密封间隙内涡流增强,从而消耗了更多的气流力能量,使气流力的阻尼增加.

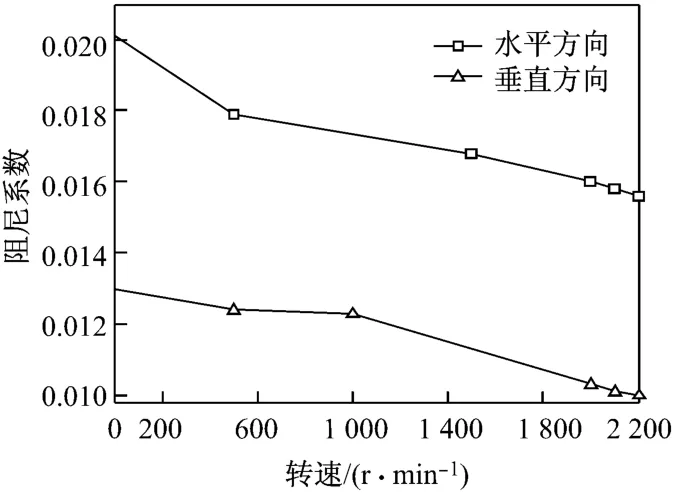
图6 气缸阻尼系数随转速变化的趋势(加气压力为0.3MPa)Fig.6 Cylinder damping coefficient vs.rotation speed(at p ressure of 0.3 MPa)

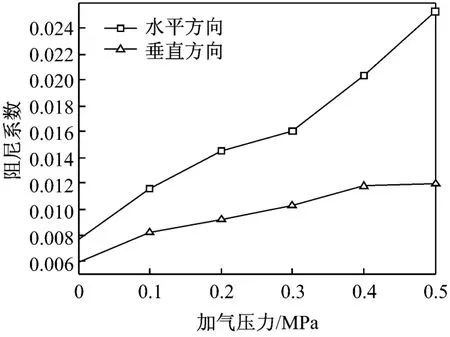
图7 气缸阻尼系数随压力变化的趋势(转速为2 000 r/m in)Fig.7 Cylinder dam ping coefficien t vs.inlet pressu re(at ratation speed of 2 000 r/m in)

5.2 气缸的共振频率

根据气缸频域响应函数的测试结果作出频域响应函数幅值谱,并分析在不同转速和压力下,密封间隙内气体流动造成的气缸共振频率偏差.图8和图9分别为在不同转速和不同充气压力下气缸频域响应函数的幅频特性曲线.从图8和图9可知：气缸水平共振频率约为15.2 H z,垂直共振频率约为22 Hz.随着转速和进气压力的变化,气缸垂直和水平共振频率的变化较小,均在2%以内,说明气体在密封间隙内流动时,对气缸系统附加质量和附加刚度的影响均比较小.

根据图8和图9的频域响应曲线,利用半功率带宽法可估算出气缸的阻尼系数.阻尼越小,则共振峰值越大,半功率频宽越小.其估算结果与对数衰减率法的阻尼计算结果相吻合.

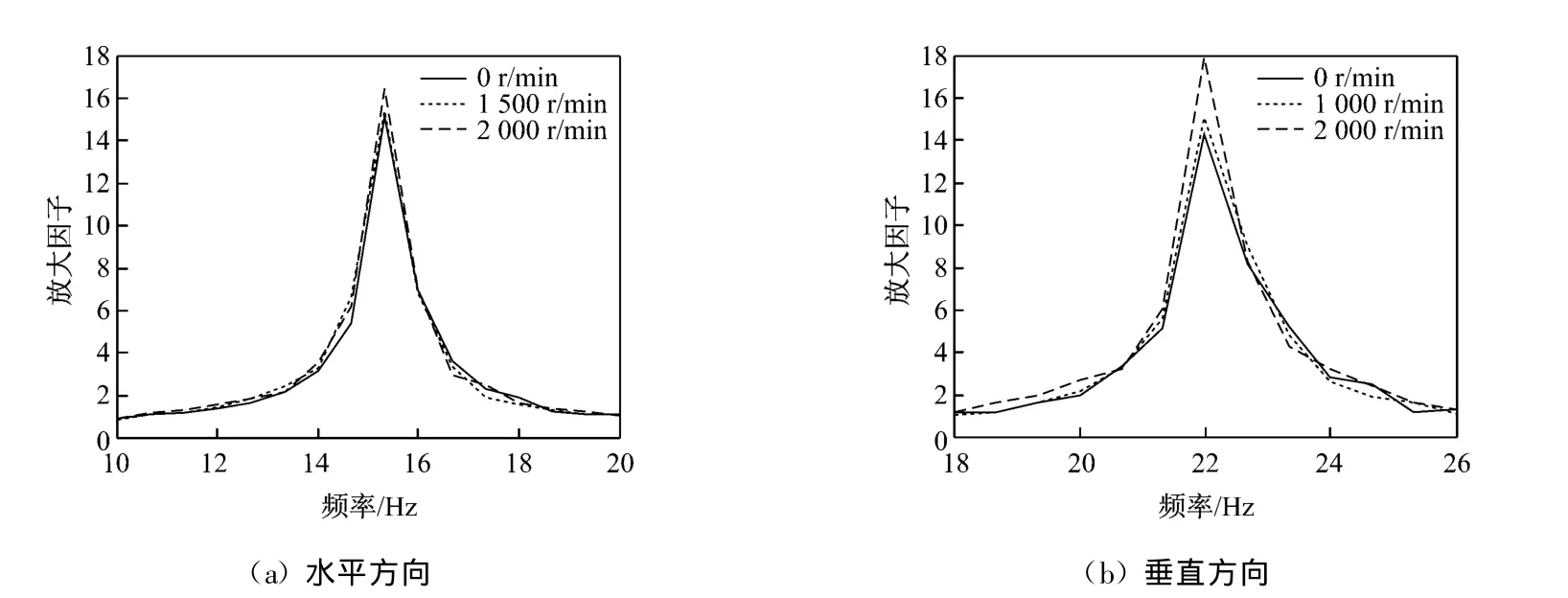
图8 不同转速下气缸频域响应函数的幅频特性曲线(压力为0.3M Pa)Fig.8 Am plitude-frequency characteristic curvesof the cylinder frequen cy response function under different rotation speed s(at p ressure of 0.3 MPa)

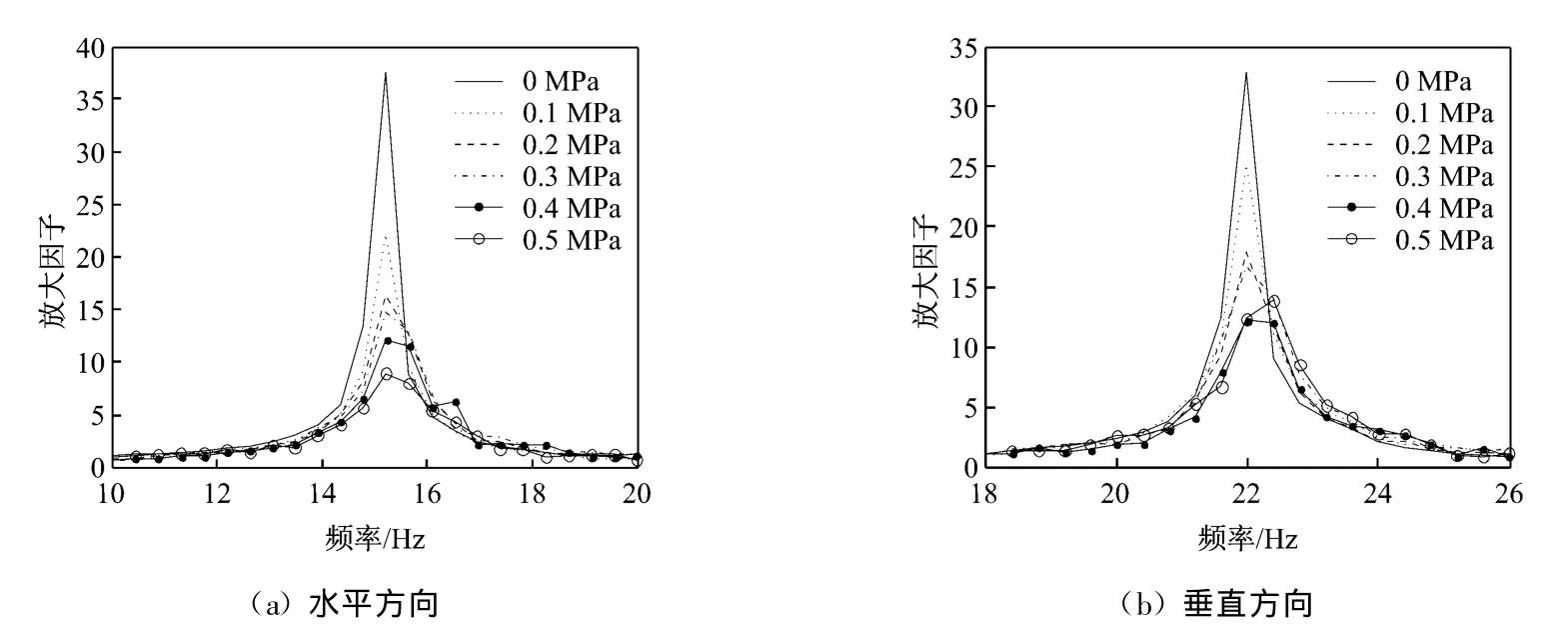
图9 不同充气压力下气缸频域响应函数的幅频特性曲线(转速为2 000 r/m in)Fig.9 Amp litude-frequency characteristic curves of the cylinder frequency response function under differen t inlet p ressures(at ratation speed of 2 000 r/m in)

6 结 论

在密封试验台上进行了试验,测试了气缸响应传递函数,研究了密封间隙内气体流动对气缸动力特性的影响.结果表明：在不同转速和压力下,充气前后气缸的共振频率变化很小,但对系统阻尼造成较大影响.随着转速的加快,密封泄漏率几乎不变,气缸阻尼系数减小;随着进气压力的提高,密封泄漏率增加,气缸阻尼系数增大.

[1] ERTAS BH.Rotordynam ic force coefficients of pocket damper seals[D].Texas：Texas A&M University,2005.

[2] 蒋浦宁.超超临界汽轮机汽流激振试验台的建立及模拟试验研究[D].上海：上海交通大学机械与动力工程学院,2005.

[3] 袁振伟,王三保,岳希明,等.涡轮阿尔福德力对转子系统动力学性能的影响[J].中国电机工程学报,2007,27(32)：77-81.YUAN Zhenw ei,WANG Sanbao,YUE Xim ing,et a l.Influences of alford force on the dynam ic properties of a turborotor system[J].Proceedings of the CSEE,2007,27(32)：77-81.

[4] 王炜哲,刘应征,陈汉平,等.迷宫轴封气流周向剪切力对转子动态特性系数的影响[J].动力工程,2007,27(5)：717-720.WANG W eizhe,LIU Yingzheng,CHEN Hanping,et a l.Effects on rotor dynam ic coefficients of circum ferential shear forces due to steam flowing through labyrinth sealings[J].Journal of Power Engineering,2007,27(5)：717-720.

[5] 韦康,叶春,葛诵,等.气隙激振力对转子临界转速的影响[J].动力工程,2006,26(1)：6-9.WEIKang,YE Chun,GE Song,et a l.In fluence of flow gap induced exciting forces on critical speeds of rotors[J].Journalof Power Engineering,2006,26(1)：6-9.