基于功率谱获取海浪波长波向算法的改进

陶 法, 马舒庆

（成都信息工程学院电子工程学院,四川成都 610225）

1 引言

随着海洋遥感技术的不断发展,基于Seasat上的合成孔径雷达（SAR）获取海浪遥感图像和无人机航拍获取海浪图像,对海洋和海洋气象发挥了越来越重要的作用。准确有效地获取海浪波长和波向,不仅对海浪预报、海洋工程,而且对反演海面风场同样具有重要意义[1]。文中主要针对利用无人机航拍海浪图像获取海浪波长和波向算法进行了研究,无人机航拍海浪图如图1所示。

2 海浪模型

根据Louguet-Higgins的理论,将平稳海况下的海浪视为平稳的具有各态历经性的随机过程,波动可看作是无限多个振幅不等、频率不等、初相位不等的简单余弦波的叠加而成。忽略波与波之间的相互作用,可得到三维随机海浪波高方程[2]:

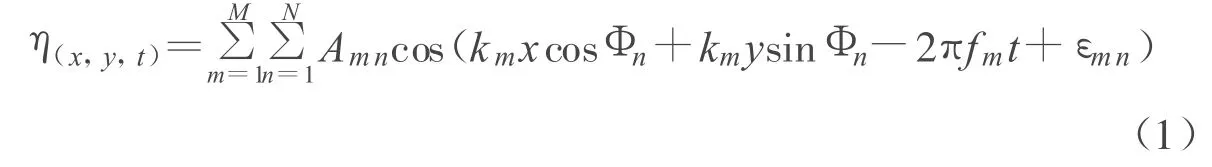
其中,m,n分别为频率分割数和方向分割数,km为波数,Φn为相对于x轴的传播方向,x,y分别表示平行和垂直于主导波传播方向的笛卡尔坐标,εmn为随机相位角,Amn为不同频率的简单正弦波的振幅,其表达式为:

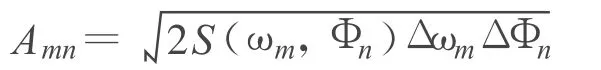
其中,S（ωm,Φn）为海浪方向谱,且 S（ω,Φ）=S（ω）G（Φ）,Δωm 、ΔΦn分别为ωm 、Φn的增量,S（ω）为频率谱函数,即不同频率间隔内的组成波提供的能量,代表海浪能量相对于组成波频率的分布,又称为能量谱,G（Φ）为方向函数。在方向函数G（Φ）一定的条件下海浪的振幅 Amn与频率谱函数S（ω）成正比关系,根据Neumann于1952年得到的一般表达式为[3]:

图1 截取达里诺尔湖的无人机航拍海浪图

其中,指数 p取 4～6,q为2～4,A和B中包含风要素（风速、风时、风距）或波高要素（波高、周期）。

基于Neumann理论Pierson-Moscowitz 1964年提出[3]:

其中 α=8.1×10-3,β=0.74,α g2=0.78。从理论上讲,S（ω）分布在 ω=0～ ∞,实际上其显著部分集中在一定频带内,其P-M谱图如图2所示。

3 基于重心坐标的改进算法

目前从海浪图像中提取海浪波长的方法主要有:二维傅里叶变换法（2D-FFT）[4]、一维傅里叶变换法（1D-FFT）[4]、基于聚类和hough变换法[5]、以及基于转动惯量[6]等方法。

3.1 2D-FFT法

方法对海浪图像进行二维傅氏变换,寻找代表海浪主频率的最大点的位置,从而求出海浪传播方向和波长。

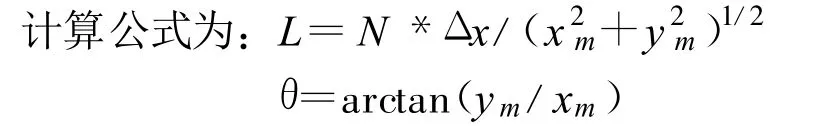
其中L,θ代表海浪的波长和方向。xm,ym是功率谱图中代表海浪主频率最大值点的坐标,N代表海浪图像的采样数,Δx代表采样间隔。

2D-FFT法比较直观,但主要缺点有:由于噪声的存在和主频不明显,极易产生误差,而用平滑法去除噪声又会引起主频位置的偏移;在计算海浪波长和方向时只用到最大值点,大部分求出来的频率分量都没有用到。

图2 P-M谱图

3.2 基于转动惯量法

假设海浪功率谱图是一个有许多离散粒子组成的薄平面,那么波浪的方向就是使这些粒子围绕某一轴的转动惯量最小的轴的方向,设该轴为y=kx,通过点（x0,y0）到直线的距离公式可得到:

那么其转动惯量为:

令转动惯量最小即dJ/dk=0,可求出:

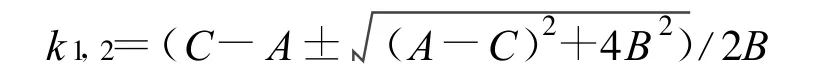
其中k1×k2=-1。k1,k2分别代表使转动惯量最大和最小的值,并舍去最大的值。再沿着这条轴的方向在某一领域寻找最大值,该最大值点的坐标就是海浪主波峰的位置,从而可以计算出波浪的波长和波向。

方法在求取方向值时较方便,但求取最大值点时同样受到噪声点和主频不明显的影响。

3.3 对2D-FFT方法的改进

从图2中可以看出在中心频率点处S（ω）最大,即由频率为中心频率的组成波提供的能量最大,可认为该频率为海浪的主频率。但在实际中海浪不是单一频率组成而且海浪的方向也不是单一方向的,由公式（1）可知每一个频率组成波对海浪的波长和波向都起一定的作用,其作用的大小由其系数值决定。所以仅以主频率计算海浪波长和波向存在误差。

3.3.1 算法实现

将波浪图像进行二维傅立叶变换得到频谱图并通过频移使其低频部分位于图像中心,（为了计算方便可以保留频谱中大于某一阈值的值,其他值设为0）。由于频谱是中心对称的所以只需选取频谱图的一半,如图3所示。

设像素点为（m×n）的频谱图中每一点坐标代表图像的频率分量可设为 f（x,y）,其值代表图像中该频率分量所占的比重可设为 A（x,y）,则由所有频率组成波提供的海浪功率谱为:

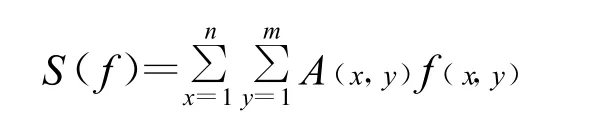
如果用某一特征频率点为 f（x0,y0）来代表所有频率点的话,则由该点计算出海浪功率谱为:

利用合力矩定理可以计算出该点坐标:

图3 提取前1024个最大值点的图像频谱图

即将图像的功率谱看成密度不均匀的薄片平面,对其求重心,所得重心的坐标即是所要求的特征频率点。

3.3.2 仿真结果

选取阈值为32点到1024点得出到中心点的距离和方向值,结果如图4所示。

从图中可以看到,随着取样点的增多计算出的方向角渐渐变小,距中心点距离渐渐变大,但变化平稳。其原因在于,随着采样点的增多图像的高频分量会相应地增多,其方向角变化趋势与海浪纹理细节的变化趋势相一致;距中心点距离变大和P-M谱中随着海浪谱的增大其主频率点向低频方向漂移相一致。

其中阈值为32点所求的重心坐标为:（x0=5,y0=13）,方向角θg=71°,其空域仿真结果如图5、6所示。

图4 基于重心法的距离值Dg和方向值θg

图5 基于重心点的空域海浪图

图6 截取阈值为32点的空域海浪图

对2D-FFT方法的改进算法的优点为:所求的f（x0,y0）点是所有频率点的重心拟合。不会造成大部分频率点用不上的问题;该重心坐标是唯一的,不会产生主频率点不明显等问题;能够根据选取的阈值合理地反映实际海浪的波长和波向。

4 分析与比较

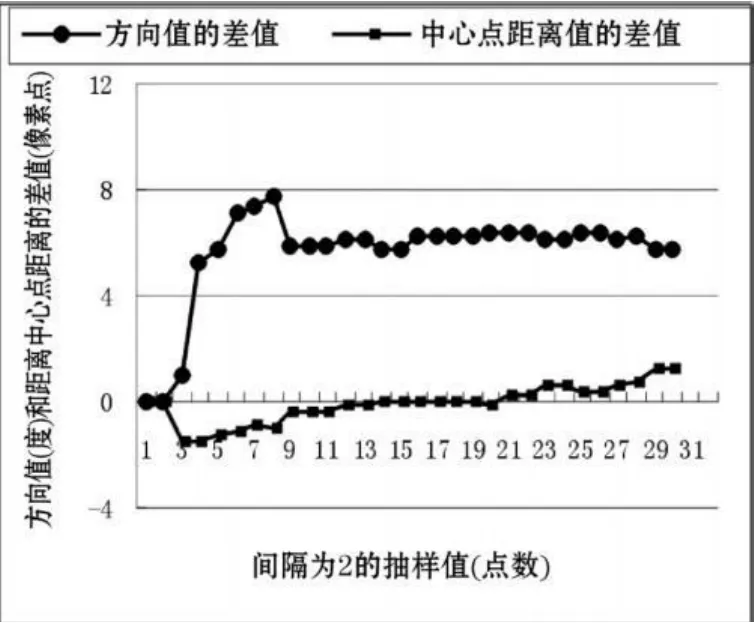
图7 基于重心法、最大值点的距离值 Δ D和方向值Δ θ

图8 基于重心法和转动惯量法的方向值

在对图1加入不同比重的盐椒噪声条件下分别基于重心法、转动惯量法、最大值法获取到中心点的距离（Dg、Dm）、方向值（θg、θI、θm）然后作比较,结果如图 9、10 所示 。

从图中可以看到:与通过最大值点求取的相应值作比较,结果是在一定范围内方向增加6°,距离增加1个像素;与基于转动惯量法所测得的方向值数据基本一致;基于最大值法求取的距离值Dm、方向值θm受加入盐椒噪声影响明显;加入盐椒噪声后基于重心法和转动惯量法获取的距离值Dg、方向值（θg、θI）基本保持不变。

图9 加入盐椒噪声下重心法与最大值法的距中心点距离值

图10 加入盐椒噪声下重心法、转动惯量法、最大值法的方向值

5 结束语

利用重心坐标法对基于图像功率谱法获取最大值点计算海浪波长、波向算法加以改进,并通过大量的试验与最大值点和转动惯量法求取的数据对比,验证了该方法计算方便、抗噪声能力强、物理概念清晰,能够更合理地表示海浪波长和波向,并有效地解决了基于二维傅里叶变换带来的主频不明显和大部分求出来的频率分量都没有用到等缺点。

[1] 陈艳玲,黄城,丁晓利.ERS22 SAR反演海洋风矢量的研究[J].地球物理学报,2007,50（6）:1688-1694.

[2] 俞韦修.随机波浪及其工程应用[M].大连:大连理工大学出版社,2003.

[3] 文圣常,余宙文.海浪理论与计算原理[M].北京:科学出版社,1984.

[4] 孙京生,刘征凯.利用SeasatSAR遥感图象分析海浪的一种新方法[J].电子科学学刊,1988,10（6）.

[5] 刘政凯,毕亚雷,黄润恒.HOUGH变换在海浪遥感图像处理中的应用[J].环境遥感,1989,6（1）.

[6] Tang Huiming,Xu Shengrong.Detection of Direction and Wavelength of Ocean Wave by Power Spectrum of Ocean Wave Image[M].Pattern Recognition,1992:164-166.

[7] Rafael C,Gonzalez.Digital Image Processing[M].Prentice Hall,2002.