丹田：机体上-下轴线对称的生命信号流系统的汇点及其反向拓扑调节

无论是古代的中医学还是道学都十分重视丹田的作用。中医学和道学理论不仅详尽地描述了丹田的位置和功能，而且也创造了许多修炼丹田以预防疾病和延年益寿的养生方法。所有这些，实在是一个不可轻易舍弃和不可不究的生物医学问题。

在中医学和道学理论中，“丹田有三，上田神舍，中田气府，下田精区。精中生气，气在中丹；气中生神，神在上丹；真水真气，合而成精，精在下丹（《钟吕传道集》）”，并且特别强调下丹田功能的重要性，认为其是任脉、督脉、冲脉三脉经气运行的起点，十二经脉也都是直接或间接通过丹田而输入本经，再转入本脏。所以下丹田是“性命之祖，生气之源，五脏六腑之本，十二经脉之根，阴阳之会，呼吸之门，水火交会之乡（《难经》）”。如此，就像许多问题一样，丹田同样是中医学留给今人的一个生物医学之谜。为了解开这一谜团，已经有一些在神经内分泌理论框架中对丹田的研究和探索。这里，我们提出的问题是：丹田是与机体上-下轴线对称并相互作用的生命信号流系统。

有关生命进化史的研究已经确认，从爬行到站立是人从动物中分化出来的一个标志，也正是站立，使人体成为一个具有上下对称性的结构，或者说这种上下对称性结构的分化是促使动物站立起来而进化为人的缘由，由此也间接地透射出这种对称性结构对于人生命活动的重要性。生物医学家们很早就认识到，在这样的一个生命对称体中，分布着许多非常重要的上下对称的内分泌器官轴系，例如下丘脑-垂体-肾上腺系、下丘脑-垂体-生殖腺系和下丘脑-垂体-肾素-血管紧张素-醛固酮系等，而在每一个内分泌器官轴系中，又包含了许多不同的非常复杂的内分泌分子轴系，这些轴系都处于人体全部生命活动的调控中心。我们相信，像这样的内分泌轴系也许还有很多，只不过我们尚未认识到而已（例如，近年来有关胃肠肽激素与下丘脑相互关系的研究提示人体中有下丘脑-垂体-胃肠轴系的存在，且这一轴系对于机体的能量平衡调节具有重要的作用）。随着生物医学技术的不断进步，这样的内分泌器官轴系或在器官轴系中的分子轴系还将被陆续发现。

从数学物理学的角度看，这些内分泌轴系可以视为一种呈上下轴线对称并相互作用的生命信号流系统。在此引入生命信号流系统是有意义的，因为由此不仅能使我们给出这些内分泌轴系生理活动的数学模型，并从中导出某些我们仅从生理学意义上难以揭示的活动规律，而且会使我们从一个全新的视角认识丹田的意义及其潜在的研究价值。

为此，我们先回顾一下信号流图理论的基本概念［1］，因为信号流图是一种用于解析信号流系统的一个极为有用的工具。

信号流图理论和方法是数学和物理学相互融合的产物。从数学的角度讲，信号流图是一种赋权的有向图，由节点以及连接在节点间的有向支路构成。根据支路的起点和终点的不同走向，信号流图可以分为开路、闭路或环及自环。根据有无环又可分为级联信号流图和反馈信号流图。根据节点和支路权的量的性质可以将信号流图分为标量信号流图和矩阵信号流图，前者节点和支路的权都是标量，而后者则每个节点所表示的是一组变量，每条支路的传输是系数矩阵。

信号流图有以下两个重要的性质：

①传输性：节点信号沿不同的出支路传输到不同的节点，到达后一节点的信号等于支路始端的节点信号乘以相应支路的传输。

t1jxj，t2jxj，……，tkjxj

②迭加性：对每一非源点，节点信号等于从其他节点来的所有信号的代数和。

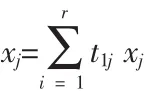
信号流图是和线性方程组以及矩阵相联系的。每一信号流图一定有唯一的方程组与之对应，信号流图的节点对应于方程组中的变量，而支路的权对应于某一变量的系数。信号流图还可以用矩阵进行描述。已经证明了的一个论断是，所有的信号流图可以分别用分支矩阵B、汇总矩阵S和支路权矩阵W三个矩阵完全地加以描述。

有三种求解一个信号流图从源点到汇点的传输（图传输）的方法。一种是基于图简化规则的方法，有四种规则能够逐步消去信号流图中的节点，最终使图简化为只包括源点和汇点的残图，而残图中从源点到汇点的支路传输就是用自变量表示应变量的系数。第二种是利用Mason增益公式，该公式是基于B、S矩阵的拓扑性质推导出来的：

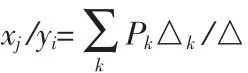
k它表明了从源节点i到节点j的传输，等于所有可能的从i到j的路传输与对应的不接触该路的图行列式积之和与图行列式之比。Mason增益公式是求信号流图中源点到汇点的传输的一个直接的方法。第三种是构成闭环信号流图。利用Mason增益公式需要找出环和路两种拓扑结构，而采用闭合信号流图只需求出环一种拓扑，更为简便，利用该方法的算法能够使分析结构复杂的信号流图的过程在计算机上实现。

矩阵信号流图的求解方法有两种，一种是利用图简化规则的逐步简化法，另一种是直接由图的拓扑结构写出传输的拓扑方法（回环法和最优拓扑法）。

信号流图另外几个重要的概念是节点分裂、回归差、部分回归差和图指数。节点分裂是指一个节点分裂为源点和汇点两个节点，在这种情形下，所有出支路离开源点，而所有入支路进入汇点，所以，节点分裂意味着阻断了通过该节点的信号传输。从节点分裂可以分别导出节点环传输、节点回归差和部分回归差的定义。图指数是指破坏图中所有的环而需要分裂的最少节点数 （本征节点），这些节点的集合构成图的最小本征集，用以表征图的复杂度。

信号流图一个很重要性质就是反向。在信号流图中，反向具有非常重要的作用，它可以简化图的拓扑结构，从而将系统从一种参数表示方式变换为另一种参数表示方式，是信号流图变换中常用的方法。存在两种反向情况，一种是从源点出发的支路的反向，另一种是从源点出发的路的反向。

以上就是信号流图的一些基本知识，对于详细的理论和方法，有兴趣的读者可以进一步参阅文献［1］。下面我们尝试利用信号流图的理论和方法来模拟人体中呈上下对称的内分泌轴系的活动。

根据生理学的研究，这些内分泌轴系中上位器官激素分子的分泌引发下位器官激素分子的分泌，是一个呈典型因果变换的生理学系统。在一个整体中，有各种不同的这样的系统在同时活动，而在每一个这样的系统中，又有各种不同的激素分子在同时活动，而这种活动在正常的生命状态下最重要的是平衡，于是，从数学的角度，这些生理活动可用线性方程组进行数学模拟。

可以从不同的水平和不同的角度构建这样的线性方程组。

把每一个不同轴系上位器官中全部的各个激素分子的分泌量作为群自变量，每个轴系各下位器官相应各个激素分子的分泌量作为群应变量，一个轴系不同位器官间激素分子的因果变换构成一个线性方程，于是所有轴系就可构成由m个线性方程组成的器官水平的线性方程组。

把一个轴系上位器官中不同激素分子的分泌量作为自变量，把其下位器官中相应激素分子的分泌量作为因变量，于是，可以构成一个轴系的n个线性方程组成的分子水平的线性方程组。

把一个轴系的n个分子水平的线性方程组复合于m个器官水平的线性方程组，这样，我们就可以构建一个具有m×n维的关于人体呈上下对称的内分泌轴系的线性方程组，这无疑是一个高维的异常复杂的方程组。进一步，考虑时间变量，则可以构建这些内分泌轴系相互作用的线性动力学方程组（线性微分方程组）。

可以看出，这些内分泌轴系的生理活动具有典型的信号流特征，是一种典型的信号流系统。器官、细胞和分子是不同水平信号流的节点，从源器官-细胞-分子到靶器官-细胞-分子是一个支路或路的传输，下位，也就是位于下腹腔的器官（细胞、分子）是信号流的汇点，所以，对应于这些轴系的m×n维线性方程组，可以用作出相应的信号流图，特别地，因为在这样的信号流系统中，每个节点都具有一组变量而非一个激素分子变量，所以，作出的将是矩阵信号流图。

信号流图的节点分裂以及基于节点分裂而产生的节点回归差或部分回归差可以视为这些内分泌轴系相应的病理过程，并且可以利用这样的方法和数据对这些病理过程进行数学模拟。

基于上述的思想，我们能够给出关于丹田的一个假说，即丹田就是人体各种上下轴线对称的内分泌轴系信号流汇点的一个数学集合，在一般情形下，这些轴系的信号流动是上下对称相互作用的，从信号流图的反向性质和作用出发，可以认为中医学创造的关于修炼丹田的方法就是对这一系统的一种反向的拓扑调节操作，其生物医学意义十分明显而重要。

［1］赵永昌.信号流图和系统［M］.北京：科学出版社，1988.