一个高维加权几何不等式

马统一

(1. 河西学院 数学系, 甘肃 张掖 734000; 2. 西北师范大学 数学与信息科学学院, 兰州 730070)

一个高维加权几何不等式

马统一

(1. 河西学院 数学系, 甘肃 张掖 734000; 2. 西北师范大学 数学与信息科学学院, 兰州 730070)

利用距离几何理论与严格的分析方法证明了一个高维加权几何不等式, 推广了文[1]建立的一个结果.

Euclidean空间; 质点集; 单形; 体积; 几何不等式

引言

本文建立如下结果:

定理1 对于中的质点集设它的占有空间维数为则有

等式成立的充分必要条件为P是的重心.

推论1 若的占有空间为则有

等式成立的充分必要条件为P是的重心.

推论2 对于中的点集设它的占有空间维数为则

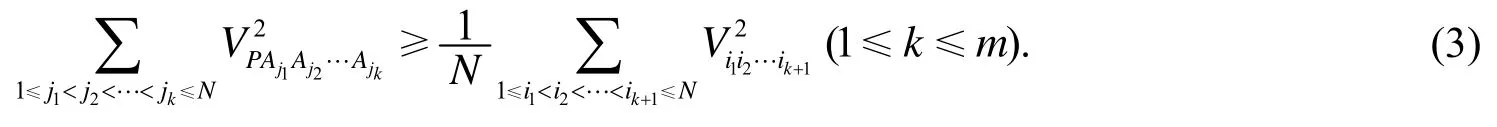
等式成立的充分必要条件为P是的重心.

推论3 对于欧氏空间中的质点集是一赋予质量的动点, 则

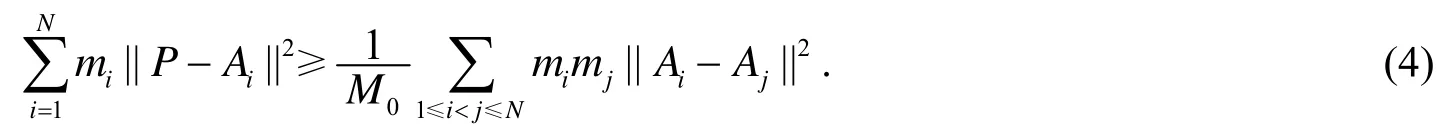
等式成立的充分必要条件为P是的重心.

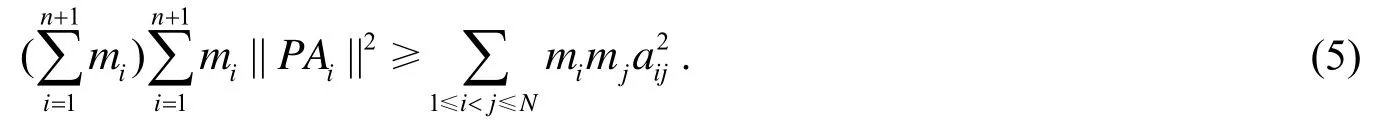
等式成立的充分必要条件为P是单形的重心.

1 几个引理

定义1中向量(0,…,0,1,0,…,0)称为单位坐标向量, 记为中任取个k扩张成的维线性子空间称为的k维坐标子空间.

引理1[1]设个点, 由它们构成单形的维体积的平方等于它们在维坐kk标子空间的正投影所构成单形的体积平方之和.

引理2 设中的质点集占有的空间维数为的自变量P有唯一驻点.

证明设的坐标为由单形体积公式, 有

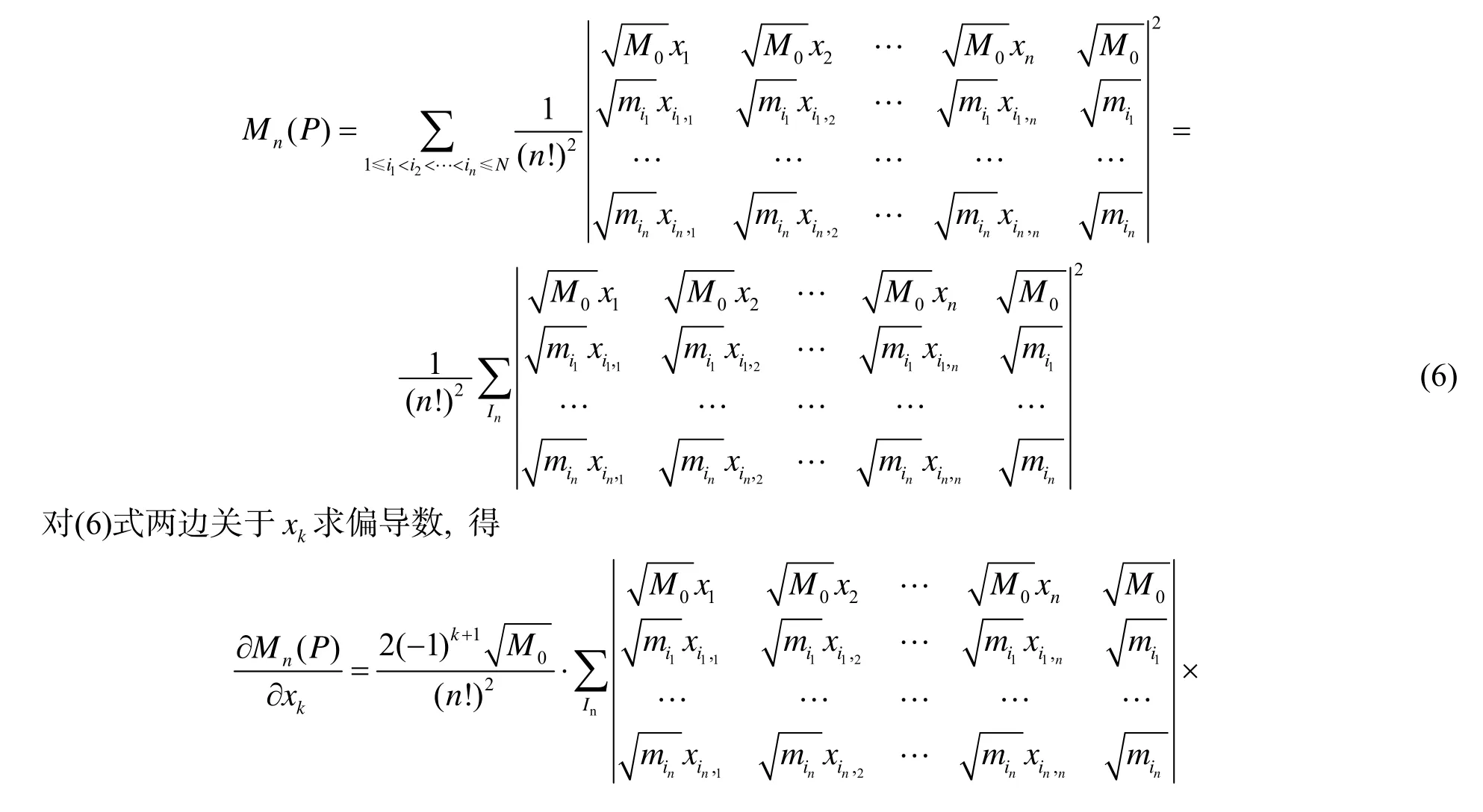
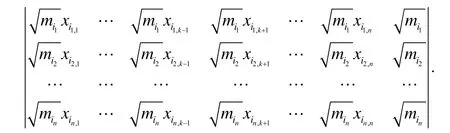
对其行列式用第一行减去第二行, 再按第一行展开, 得

2 定理的证明

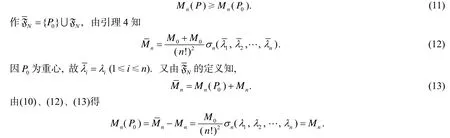
再由(11)式即知推论1成立.

定理1及其推论有许多精彩的应用, 限于篇幅, 将另撰文介绍.

[1] 刘 立, 周加农. 一个经典不等式的高维推广[J]. 数学季刊, 1988, 3(2): 99～103

[2] 张景中, 杨 路. 关于质点组的一类几何不等式[J]. 中国科学技术大学学报, 1981, 11(2): 1～8

[3] 马统一. Veljan-Korchmaros型不等式的稳定性[J]. 数学年刊, 2008, 29A(3): 399～412

[4] 苏化明. 一类涉及两个单形的不等式及应用[J]. 数学研究与评论, 1995, 15(3): 429～435

[5] 王卫东. 单形内任一点的一个含参不等式[J]. 数学杂志, 1999, 19(4): 391～396

[6] 马统一. 关于高维单形的一个不等式及应用[J]. 数学的实践与认识, 2000, 30(4): 508～512

[7] 冷岗松. 关于Gerber不等式的一个猜想[J]. 数学研究与评论, 1996, 16(4): 561～564

A Weighted High-Dimensional Geometric Inequality

MA Tong-yi
(1. Department of Mathematics, Hexi Institute, Zhangye 734000; 2. College of Mathematics and Information Technology, Northwest Normal University, Lanzhou 730070, China)

We use the distance geometric theory and rigorous analysis method to prove a weighted high-dimensional geometric inequality, which extends a known result in[1].

Euclidean space; set of particles; simplex; volume, geometric inequalities

O178

A

1672-5298(2010)03-0001-05

2010-05-29

国家自然科学基金资助项目(10971128); 甘肃省教育厅研究生导师基金资助项目( 0709-03)

马统一(1959 - ), 男, 甘肃会宁人, 甘肃河西学院数学系教授. 主要研究方向: 凸几何分析、距离几何和离散几何