倾斜因子对夫琅禾费衍射强度的影响

李芳菊,耿森林,文 军,秦玉伟

(渭南师范学院物理与电子工程系,陕西渭南714000)

倾斜因子对夫琅禾费衍射强度的影响

李芳菊,耿森林,文 军,秦玉伟

(渭南师范学院物理与电子工程系,陕西渭南714000)

利用傅里叶光学详细讨论了斜入射情况下的夫琅禾费衍射,导出了大角度斜入射和衍射下的光强理论分布,分析了倾斜因子对衍射花样的影响.利用该理论对平行光斜入射光栅衍射实验的衍射花样进行了理论模拟,理论与实验基本相符.

倾斜因子;夫琅禾费衍射;光栅衍射

1 引 言

许多文献[1-2]对平面光波斜入射衍射物产生的衍射光场特性进行了讨论,但有些文献[1,3-4]讨论的是条纹位置和级次分布特征,并没有对衍射光强做分析;有些文献[2,5-6]中虽然涉及到各衍射级的光强,但并没有考虑倾斜因子的影响.多数物理光学教材[7-8]在讨论衍射光强分布时,都限制在近轴小角度衍射,此时倾斜因子为常数,对各级光强的影响可以忽略;也有文章[9-12]仅限于垂直入射下的大角度衍射作了理论阐述;文献[12]分析了仅限于垂直入射单缝时倾斜因子对光强的影响.本文从标量衍射理论出发,分析了倾斜因子在夫琅禾费衍射中所起的作用,得出了带有倾斜因子的光强分布公式,并实验上观察到了平行光斜入射光栅时的衍射光强的不对称,利用Matlab扫描衍射花样得到的光强实验数据分布和理论分布曲线进行比较,二者吻合较好.

2 考虑倾斜因子时的夫琅禾费衍射公式

标量衍射理论的亥姆霍兹-基尔霍夫衍射公式为[8]

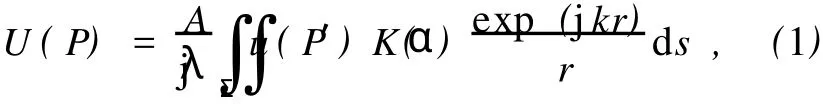
如图1,Σ为开着的衍射孔径,r′为入射光源S到Σ上一点P′的径矢,r为观察点P到P′的径矢;n为P′所在位置Σ的外法向[7].(1)式中U(P)为空间观察点P的复振幅,u(P′)为衍射孔径上P′点的复振幅,为倾斜因子,cos(n,r′)为入射光与衍射孔径外法向夹角余弦,cos(n,r)为出射光与衍射孔径外法向夹角余弦.

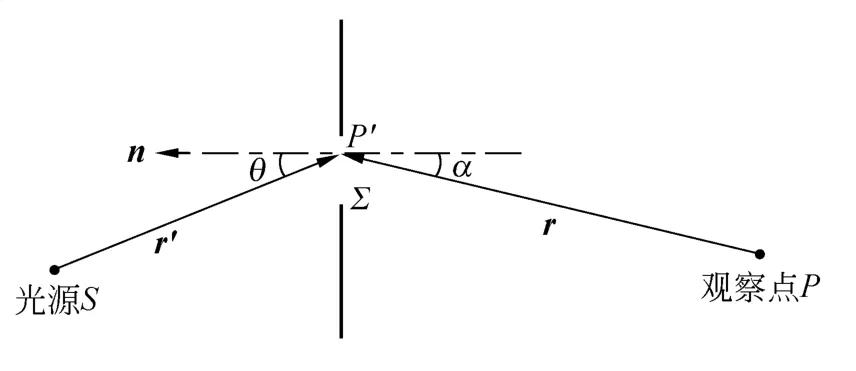
图1 点光源照明平面衍射屏

下面以一维分布的衍射孔径为例,对K(α)和r进行分析.

如图2,孔径所在坐标轴为X,平行光以角度θ入射,即入射光与衍射孔径任意P′位置的外法向夹角不变,都是π-θ;α为衍射角,对于夫琅禾费衍射,考虑的是衍射孔径各子波波源发出的平行衍射光在透镜后焦面上的相干叠加,即到达观察点的光场来自于衍射孔径沿衍射方向的平行光,对于某一观察点P,出射光与衍射孔径外法向夹角为α.因此cos(n,r′)=-cosθ,cos(n,r)= cosα,即与衍射积分区Σ无关,在(1)式中倾斜因子可以提到积分号外面去,

则(1)式可表示为

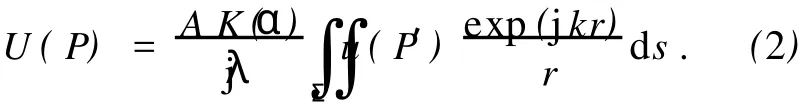
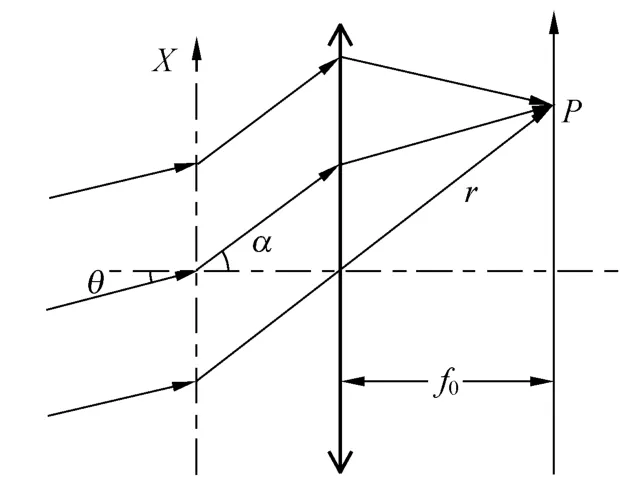
图2 夫琅禾费衍射原理图

如图3所示,孔径上P′坐标为x,观察点P到P′的距离为r,P到衍射屏所在坐标原点O的距离为r0,z为衍射屏到观察屏之间的距离.则

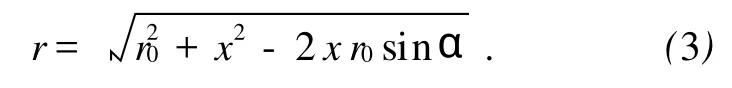
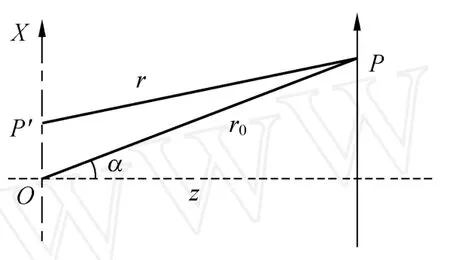
图3 平面屏一维孔径的衍射

在衍射屏通光孔径远小于r0的条件下,(2)式分母中的r用r0代替,(3)式展开并忽略高次项和二次项,则:

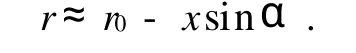
由以上分析,最终(1)式可以写为

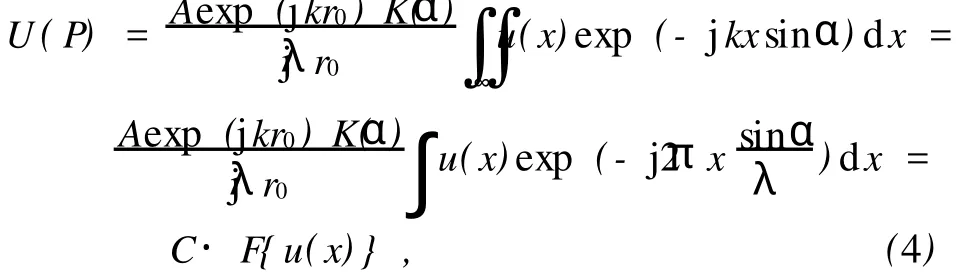
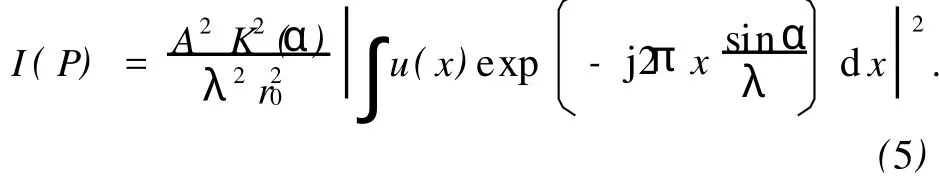
由以上分析可知,夫琅禾费衍射花样的光强和K2(α)成正比,和成反比,K(α)是随衍射角α增加而单调减小的函数.所以倾斜因子对衍射花样的强度分布起调制作用,同时对各级亮纹中心位置也有微小的影响.在近轴夫琅禾费衍射情况下,K(α)≈1,r0≈z,正负衍射级次光强相同;在大角度斜入射或者大角度衍射情况下,特别是高频光栅的衍射,各级次的衍射角有很大的变化,此时倾斜因子的作用不可忽略.

3 平行光斜入射光栅衍射实验

设衍射屏的透过率函数[8]为

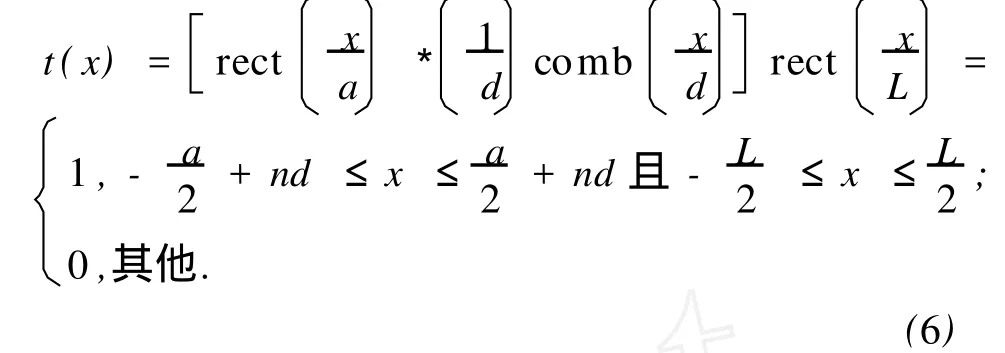
式中a是透光缝宽,d为光栅常量,n为整数,L为光栅有效宽度.

设入射光为单位振幅,如图4,θ为平行光入射角,入射光在衍射孔径前表面的复振幅分布为

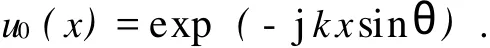
则透过衍射屏的光场为

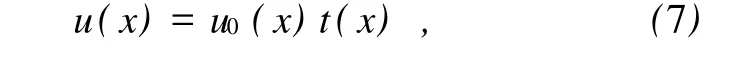
把(7)式代入(4)式,求出透射光场的衍射光场为

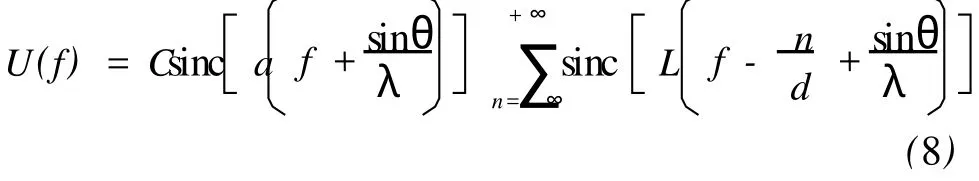
其中f=sina/λ.光强为

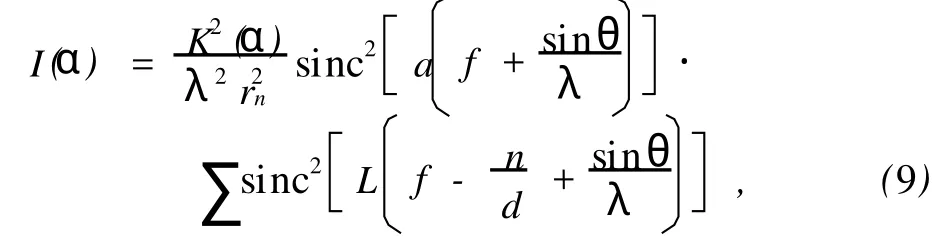
实验中接收屏与入射光垂直,θ=60°,d= 10-2mm,L=4 cm,傅里叶透镜焦距f0=30 cm,入射光为He-Ne激光(632.8 nm),部分衍射花样如图4.可以看到,±1级强度不对称,由(9)式理论计算得到±1级衍射光斑强度之比为利用Matlab对衍射图样进行处理,扫描得到相对强度分布如图5,图6为根据式(9)的强度理论分布曲线.

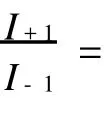
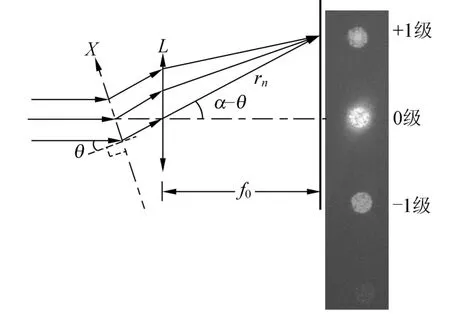
图4 平行光斜入射光栅衍射花样

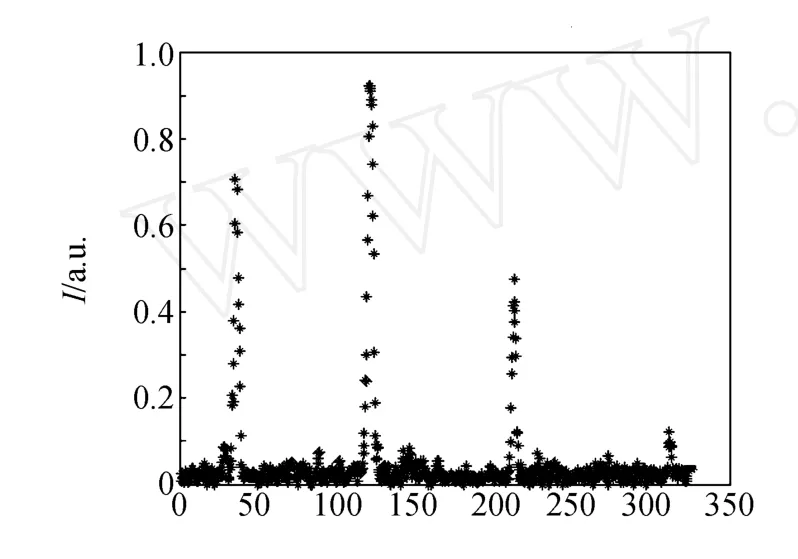
图5 光强实验数据分布图

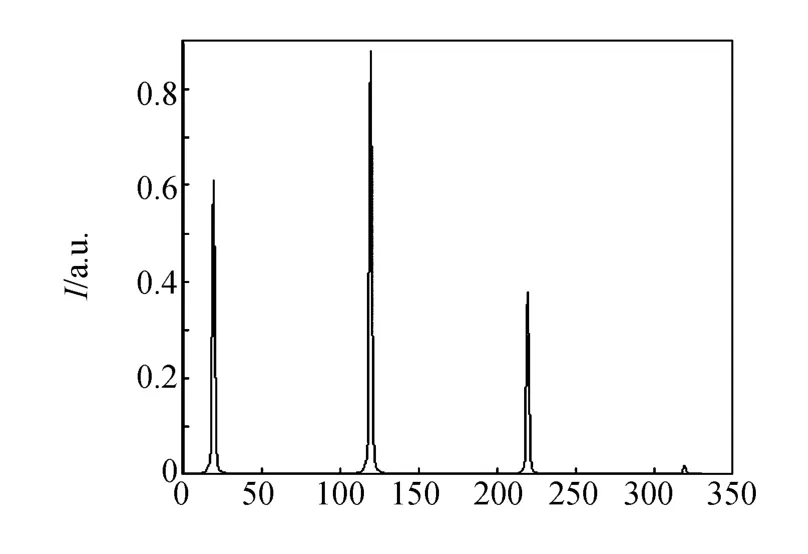
图6 光强理论分布曲线

由图5～6可以看出,平行光斜入射光栅衍射的实验扫描得到的强度分布与理论分析得到的强度分布情况基本吻合,说明倾斜因子的分析理论是合理的.

4 结束语

1)通过实验观察到:平行光斜入射光栅时,不仅衍射条纹级数、正负级次位置不对称,而且正负级次强度也不对称;斜入射角度越大,不对称越明显.

2)利用标量衍射理论分析了斜入射情况下光栅的夫琅禾费衍射,得到斜入射的夫琅禾费衍射强度的理论分布公式.利用该理论对大角度斜入射光栅情况下的夫琅禾费衍射花样的强度不对称进行了分析,将衍射强度的理论分布曲线和实验扫描结果进行对比分析,理论分析与实验结果基本吻合.

3)在实验中发现:对于比较宽的单缝或者低频光栅(十几线每毫米),各衍射级次限制在较小角度范围之内,即使在较大角度斜入射情况下正负级次强度几乎相当,即倾斜因子对各级强度的影响较小;对于高频光栅(几百线每毫米以上),各衍射级次分布在很大的角度范围内,特别是在斜入射时对应正负级次的强度对比很明显,若作为“研究倾斜因子对衍射强度的影响”的演示实验具有很强的可观性.

[1] 王琪琨,张兆钧.斜入射光波的光栅衍射研究[J].大学物理实验,1999,12(2):27-28.

[2] 吴逢铁,江新光.衍射轴棱锥产生光学点阵的理论和实验[J].光学学报,2008,28(12):2 250-2 254.

[3] 李亚玲,李文博,李宓善,等.光栅衍射和布拉格公式[J].大学物理,2005,24(9):30-32.

[4] 宋超群,李国安.斜入射光栅衍射条纹的分布[J].高师理科学刊,2003,23(3):86.

[5] 陈德伟,李永平.光束斜入射的分频光栅衍射行为研究[J].强激光与粒子束,2004,16(2):163-166.

[6] 吕春梅,苏为宁,潘永华.不同结构光栅的衍射光强分布[J].物理实验,2008,28(2):42-46.

[7] 玻恩M,沃耳夫E.光学原理[M].北京:科学出版社,1981:522-529.

[8] Goodman J W.Introduction to Fourier optics[M]. New York:McGraw-Hill,1968:39-40,69-71.

[9] 孙桂林.夫琅禾费衍射与大角度衍射[J].光学技术,2008,34(3):466-468.

[10] 厉江帆,单树民,黄春佳,等.夫琅禾费近似与夫琅禾费衍射测量的准确度[J].光学技术,2001,27 (5):472-477.

[11] 朱湘柱,曾阳素.衍射理论公式的诠释与应用[J].大学物理,2007,26(10):27-30.

[12] 相凤华,张继县.倾斜因子对单缝夫琅禾费衍射强度的影响[J].廊坊师范学院学报,2003,19(4): 89-91.

Impact of inclination factor upon the Fraunhofer diffraction pattern

LI Fang-ju,GENG Sen-lin,WEN Jun,QIN Yu-wei
(Department of Physics,Weinan Teachers University,Weinan 714000,China)

The theory of Fourier optics is applied in the analysis of incident wave.For large angle incidence and diffraction,theoretical intensity distribution of the diffraction pattern is obtained.The impact of inclination factor upon the Fraunhofer diffraction pattern is discussed in some detail.Subsequently,the diffraction intensity is investigated theoretically and experimentally.A combination of theory and experiment is proposed to trace out grating diffraction pattern.The theoretical analysis and experimental results are in good agreement.

inclination factor;Fraunhofer diffraction;grating diffraction

O436.1

A

1005-4642(2010)10-0033-03

[责任编辑:郭 伟]

2010-01-28;修改日期:2010-06-28

渭南师范学院科研基金项目(No.08YKZ038),渭南师范学院教改项目(No.J G200922)

李芳菊(1975-),女,陕西渭南人,渭河师范学院物理与电子工程系讲师,硕士,主要从事声光检测方向研究.