气轨阻力与速度关系的研究

贺卓然

(北京大学物理学院,北京100871)

气轨阻力与速度关系的研究

贺卓然

(北京大学物理学院,北京100871)

在气轨上测量了微小阻力和速度的关系.通过振动能准静态衰减的假设建模,并利用一种改进的线性拟合方法做数值微分,最终在3台气轨上得出了一致的经验规律:

气轨;阻力;速度

1 引 言

气轨是低阻力装置,在大学物理实验中应用广泛.因而研究气轨阻力与速度的关系对分析和修正气轨上的动力学实验的误差具有重要意义.但由于气轨上的阻力很小,滑块即使长距离地单程滑行,其速度也没有明显改变.这么小且与速度有关的力,测量起来绝非易事.本文采用滑块在气轨上做阻尼振动的实验[1-4]来完成测量,去掉先验假设f(v)∝v后,得到了新的结果.

2 实验原理

滑块在气轨上的运动方程为

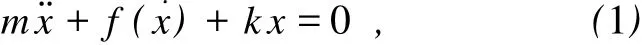
虽然f(v)的表达式未知,但Weierstrass证明过定理[5]:任何一个闭区间上的连续函数,都可以用足够高次的多项式一致逼近.因此可以把f(v)在实验数据范围[0,vmax]内近似写成N次多项式pN(v).理论上只要N足够大,用pN(v)近似f(v)就可以足够精确.于是有然而,若直接把f(v)代入(1)式,所得微分方程将高度非线性,解析解近乎不可能.但由于阻力f (v)很小,可以采用振动能准静态衰减的近似,即1个周期之内,滑块的运动仍近似满足无阻尼时的x=Asinωt,v=v0cosωt,其中v0是滑块过平衡位置的速度,易用光电门测得.于是从平衡位置出发,经过1个周期之后,振动能改变量为

其中B为Beta函数.这里假设了能量衰减几乎完全由气轨阻力引起,而忽略了诸如弹簧发热等其他因素引起的能量损失.这样方程(1)中的f才代表要研究的气轨阻力.

由于阻力f很小,振动能衰减缓慢,可以用微分近似代替差分,将衰减过程连续化,得

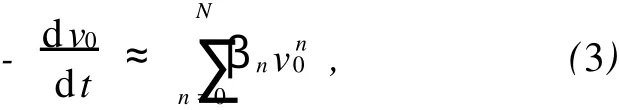
其中

不过,在实验中N并非越大越好,因为测量总有随机误差,太大的N导致曲线pN(v)剧烈抖动.而实测曲线本身比较光滑,故本文中取N=3,且后面拟合时零截距的假设α0=β0= 0也得到了实测数据的支持.

3 实验及结果

3.1 Hooke定律的验证

前面假设了没有阻力时滑块做简谐振动x= Asinωt.这是Hooke定律的结果.但实际使用的弹簧是否满足Hooke定律,则有待实验检验.

图1 验证Hooke定律

在气轨的边缘固定摩擦尽可能小的定滑轮.用细线一端拉住弹簧振子,另一端绕过定滑轮拉住砝码盘的挂钩.在盘中放入不同质量m的砝码,用气轨上的标尺读出最大静摩擦允许的最大平衡范围[x1,x2],记录实验数据并计算其中心位置x=(x1+x2)/2如表1所示.

表1 Hooke定律的验证

从表1看出,当砝码B质量增加时,滑轮轴承处的最大静摩擦fmax增大,滑块A的平衡范围[x1,x2]越来越宽,但只要弹簧弹力F=F(x)在小范围[x1,x2]内近似线性,则在[x1,x2]的中点x=(x1+x2)/2处恰好有摩擦为0,F=mg.故要验证Hooke定律,只需验证x是否与砝码总质量m成线性关系即可.作图并拟合发现x与m的线性相关程度高达r =0.999 9,说明实验所用弹簧在很大的振幅范围内仍高精度地满足Hooke定律.交换k1和k2的位置,重复上述实验,线性关系依然成立.

3.2 气轨启动前的测量

U挡光片一、三挡光边距离δl=10.30 mm;滑块与挡光片总质量m1=449.43 g;两弹簧总质量m2=22.37 g;振子等效质量[1]m=m1+m2/3 =456.89 g.

从后面的实验步骤不难看出,本部分的测量结果不影响f(v)曲线的形状,而只改变其标度.

3.3 气轨上的测量

1)光电门定位于气轨上滑块的平衡位置.

2)在弹簧的弹性限度内,尽可能大地拉开滑块后释放.待滑块振动几个周期稳定后,开始采集数据.在滑块振幅衰减的不同阶段,重复如下过程若干次.

设滑块上U型挡光片连续5次“左→右”通过平衡位置的10个挡光时刻为:t11,t12,t21,t22,…,t51,t52.规定t11=0,记录ti1和δti=ti2-ti1于表2中.表2共记录了8组数据.

0ii斜率dv0/dt,作为处的导数(详见第5部分讨论).

用所得回归直线方程给出t时刻对应的速度值,作为v0.于是完成表3.

图2 实测数据点的多项式拟合

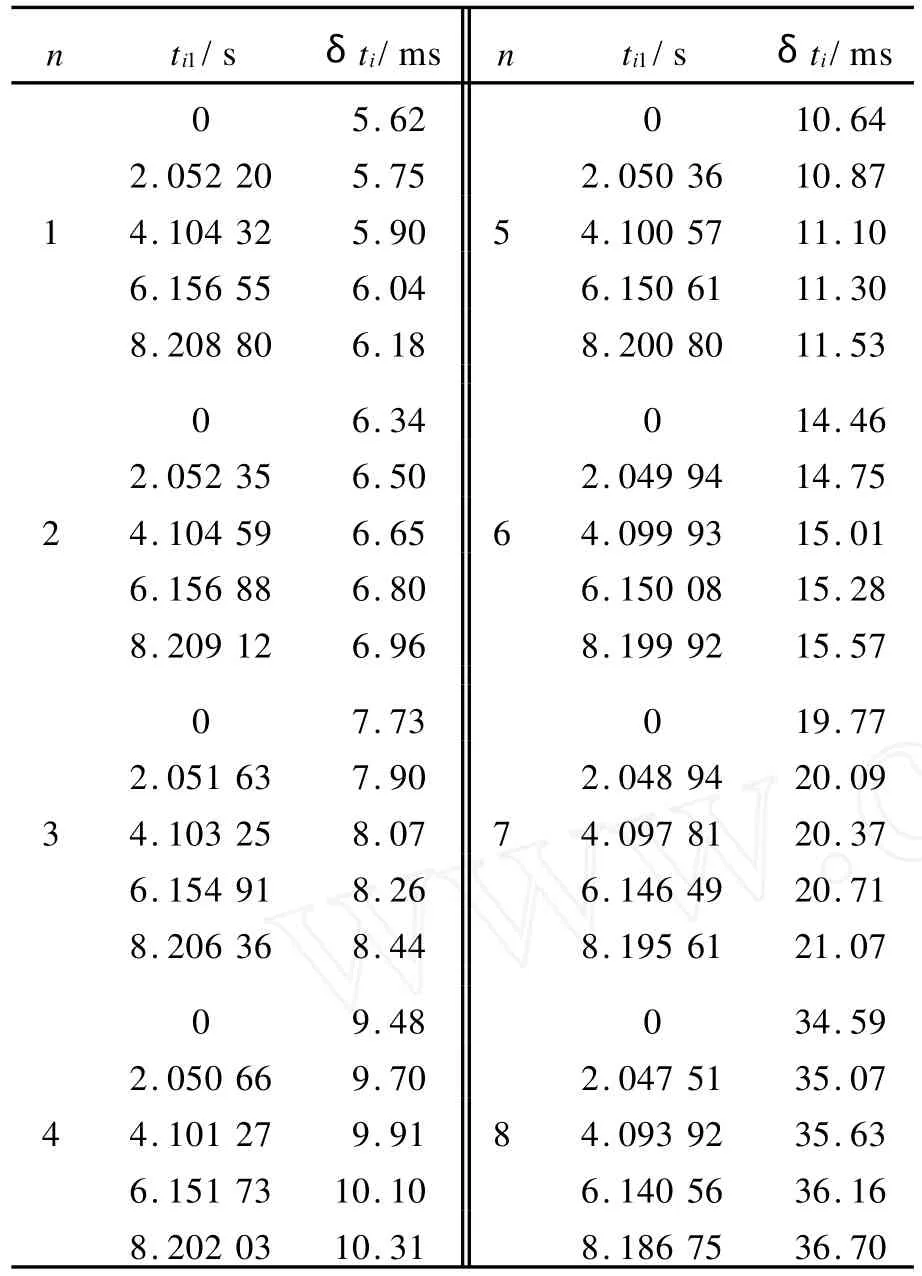
表2 气轨阻力-速度关系测量数据

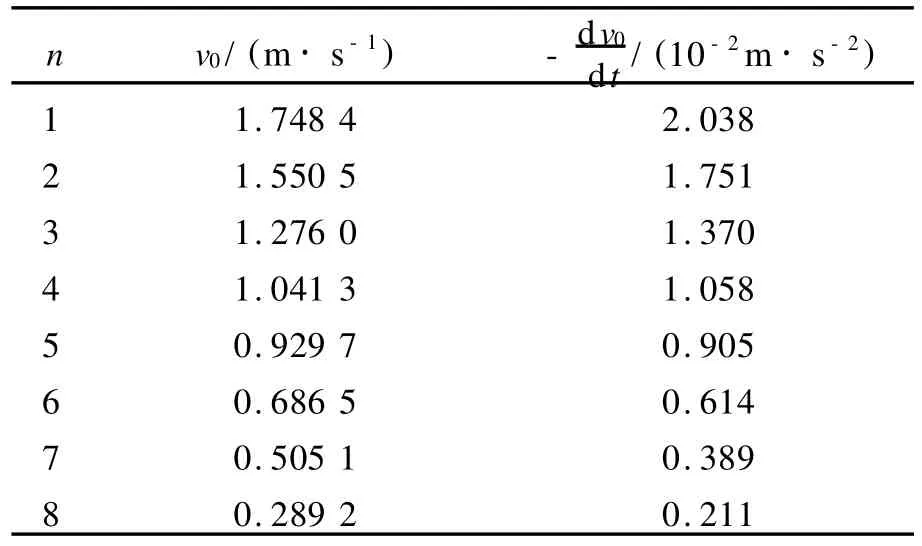
表3 计算结果

求出各项系数βi后,不难算出各αi值.于是有f(v)≈p3(v)=(4.95v+6.33v2-1.62v3)× 10-3N,其中v的单位为m/s.这样就得到了f(v)在实验数据范围0～1.8 m/s的3次多项式逼近结果p3(v).

4 结果分析

在0～1.8 m/s范围内,p3(v)曲线与f(v)近似重合.于是作p3(v)的图像(如图3所示).由图可知,气轨阻力速度关系f(v)确实不像Stokes公式描写的正比关系那么简单.当v较小时, f(v)表现出明显的向上弯曲.当v较大时曲线却比较直.在另外2台气轨上重复实验,也得到了这种向上弯曲且前弯后直的f(v)曲线.

如果能定量描述这一由曲变直的规律,就可能得到f(v)的经验公式.根据p3(v)曲线,笔者猜测f(v)可以写成如下形式:

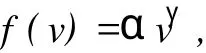
其中幂指数γ可能不是整数.在这个参数模型下,重复第2节中的推导不难得到

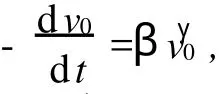
双对数拟合常常在数据小的一端误差大,从图4已经可见一斑.为得到更可靠的γ值,笔者放弃了取对数,而直接采用非线性最小二乘拟合,得γ=1.29,f(v)=9.59v1.289×10-3N,发现在0～1.8 m/s范围内,f(v)(图3中的点)确实与p3(v)几乎完全重合.这一定程度上验证了前面猜测的f(v)模型.在另2台气轨测得γ=1.27和γ=1.33,故3台气轨所得γ平均值为1.30. 3个幂指数十分接近,进一步肯定了经验规律的可靠性.

图4 实测数据点的双对数拟合

5 讨 论

本实验的数据处理涉及到微分的计算.为了减小误差,本文采用了把数据点(xi,yi)的线性拟合的斜率归结为的导数的方法.下面介绍此方法的依据.

设实验中密集测量了若干个数据点(xi,yi).它们分布于1条未知的光滑曲线y=f(x)附近.

在足够小的区间[x0,x0+δ]内,曲线y= f(x)近似为直线.对区间内的点用线性拟合,得出斜率的最佳无偏估计

考虑曲线在区间[x0,x0+δ]内的微弯曲,将f(x)在x0处泰勒展开到二阶,有yi=a+bxi+

令

则这表明在只考虑到二阶泰勒项的精度下,线性拟合的斜率^b是xp处导数f′(xp)的无偏估计.

用文献[6]中的统计理论可以证明,即使对测量数据点做二次拟合y=a+bx+cx2,xp点处的导数b+2cxp的不确定度也是最小的,且其值等于线性拟合的结果.因此完全不必做二次拟合,它起不到改进结果的作用.

6 结束语

本文去掉f(v)∝v的假定后,通过基于振动能准静态衰减假设的一系列合理的近似,成功处理了一个非线性系统的实验测量问题.在数据处理过程中,本文通过Weierstrass的多项式逼近手段,并采用一种改进的线性拟合方法做数值微分,在尚未对f(v)建立任何先验的参数模型的情况下,便得出了与最终结果十分接近的f(v)曲线.最后根据曲线,笔者猜出了一个与实测数据高度吻合的参数模型并在3台气轨上得到了一致的幂指数γ≈1.30.

感谢北京大学物理学院实验中心的各位老师提供的支持与帮助.

[1] 吕斯骅,段家忯.新编基础物理实验[M].北京:高等教育出版社,2006:113-116.

[2] 段玉玲.复测法测定气轨的粘性阻尼常量[J].物理实验,2001,21(4):41.

[3] 毛全宁,葛宇宏.粘滞阻力和光电计时器引起的气轨系统误差[J].技术物理教学,2004,12(4):26.

[4] 王亚辉.气轨上简谐振动测弹簧劲度系数[J].大学物理实验,2006,19(3):11.

[5] 周铁,徐树方,张文平,等.计算方法[M].北京:清华大学出版社,2006:23.

[6] 王松桂,陈敏,陈立萍.线性统计模型:线性回归与方差分析[M].北京:高等教育出版社,1990:34.

Relationship between resistance and velocity on air track

HE Zhuo-ran
(School of Physics,Peking University,Beijing 100871,China)

A method to determine the relationship between resistance and velocity on an air track is designed.By using approximations based on the assumption of quasi-static oscillation energy loss and an improved linear regressive method for numerical differentiation,an empirical law is obtained:,whereγ≈1.30.

air track;resistance;velocity

O311.1

A

1005-4642(2010)12-0039-04

[责任编辑:郭 伟]

2010-03-03;修改日期:2010-05-15

贺卓然(1990-),男,湖北武汉人,北京大学物理学院2008级本科生.