井灌区降水量的特征分析及灰色预测

2010-09-19薛明霞李洪建王学萌

山西农业科学 2010年11期

王健，孙明，薛明霞，李洪建，王学萌

（1.山西大学环境与资源学院，山西太原030006；2.山西省水文水资源勘测局太谷均衡实验站，山西太谷030800；3.山西大学黄土高原研究所，山西太原030006；4.山西省农业科学院农业资源综合考察研究所，山西太原030006）

灰色模型作为一种预测理论，已经在各行各业得到充分的应用，探索其在水文预测中的应用具有现实的意义[1]。其中，王学萌[2]和郝永红[3]等把灰色理论预测模型应用到泉流量和人口方面的研究取得了很好的效果。针对降水量变化随机性强、受外界影响因素多、难以准确地用非线性函数加以描述等特点，本研究提出采用灰色理论预测模型对太原盆地井灌区降水量在中、短期的变化进行预测。通过对实例建模分析，并进行误差检验，达到精度要求，可用于年降水量的预测，这对农业生产、生活有重要作用。此外，降水量预测精度的提高，对本研究区地下水可开采量的确定也具有重要的意义。

1 区域概况

研究区域为农业井灌区，位于山西省太原盆地中部，地理位置为东经112°30′～112°33′，北纬37°26′～37°27′，面积7.72 km2。该区域涉及10个自然村，万余人，万余头牲畜，耕地540余hm2，农用地下水开采井9眼/km2，主要种植冬小麦、玉米、谷子、高粱、大豆、秋杂粮、棉花、油料、蔬菜及瓜类等10余种作物，属纯井灌溉区。

1.1 水文气象条件

太原盆地井灌区属大陆性干旱半干旱气候，多年平均气温为9.9℃，7月份最高，1月份最低；多年平均降水量417.2 mm，主要集中在6—9月份；多年平均水面蒸发量1 002.9 mm（标准E601蒸发器测定）；最大冻土深度为92 cm，全年无霜期200 d。

1.2 水资源特征

太原盆地井灌区及周边地区无地表水体，工农业生产及人畜吃水均依靠开采地下水。北部边界为汾河支流乌马河，是一条间歇性河流，上游建设有中型水库，一般年份无弃水，丰水年份有水流过。不同频率年的降水量为：P=20%，降水量508.2 mm；P=50%，降水量 403.6 mm；P=75%，降水量331.5 mm；P=95%，降水量246.6 mm。地下水可开采模数为19.2万m3/（年·km2）。

2 研究方法及主要模型

2.1 降水量特征分析

以太原盆地井灌区1954—2007年（54年）的年降水量作为研究对象，资料来自于太谷县气象站和太谷水文均衡实验站。运用滑动平均法进行趋势分析（图1-A）得出，近54年降水量呈递减趋势。在年际变化上，除个别年份外，1954—2007年平均降水量的年际波动幅度不是很大，基本上在400 mm左右，降水量的最小值为219 mm，出现在1986年；最大值出现在1977年，降水量为621.2 mm。以11年为基准，把54年的数据分为5段。从图1-B可以看出，1987—1997，1998—2007年2个年份段降水量明显减少，1987—1997年降水量最少；1954—1964年平均降水量最多。从分段结果来看，降水量也呈现出明显的减少趋势。

表1为太原盆地井灌区1954—2007年各月降水量的描述性统计结果。根据变异系数（CV）的大小可以粗略估计变量的变异程度，CV≤10%属于弱变异性，10%≤CV≤100%属于中等变异性，CV≥100%属于强变异性。由表1可知，多年各月降水量均有较大变动，其中12，1，2月份属于强变异性，其余各月的多年平均降水量属于中等变异性，其中3，11月的CV均为96%，接近于强变异性，由此说明，冬季各月的降水量多年波动较大。

太原盆地井灌区降水年内分配极不均匀，起伏较大。1954—2007年全年降水量71.23%集中在6—9月份，并多以大雨和暴雨形式出现，夏季降水量往往集中在几场降水之中（图2）。由图2可知，1954—2007年太原盆地井灌区各月平均降水量呈典型的正态分布，7月降水量达到最大值，为93.4 mm，其比例为22.39%；1月降水量达到最小值，为2.7 mm，其比例为0.65%；冬季（12，1，2月）降水量最少，多年平均 12，1，2月份降水量占全年降水量的1.49%。冬夏降水量悬殊，全年降水量明显集中于夏季。

表1 1954—2007年太原盆地井灌区降水量统计 mm

2.2 年降水量的突变分析

对太原盆地井灌区53年（1954—2006年）的年降水量时间序列，采取滑动的方法连续设置基准点，并确定基准点前后2个子序列的样本数相同，即n1=n2=10，用滑动t检验法计算统计量t（用来检验2个随机样本平均值的显著性差异）。为此，我们把一连续的随机变量分成2个子样本集 x1和 x2，μi，Si2和 ni分别代表 xi的平均值、方差和样本长度（i=1，2）。其中ni需要人为定义。

原假设 H0：μ1－μ2=0，定义一统计量为

这里 sp2是联合样本方差，sp2=为 σ2的无偏估计，显然，t0～（tn1+n2-2）分布给出信度 α，得到临界值tx，计算t0后在H0下比较 t0与tα，当 t0≥tα时，否定原假设，即说明其存在显著性差异，当 t0＜tα时，则接受原假设H0。具体应用时，结合具体的需要选择ni，并不断地变动ni，以增进检查结果的可靠性[4]。

本次检验把太原盆地井灌区年降水量作为样本，经多次试验选择ni=10，代入（1）式，检验结果列于表2。太原盆地井灌区年降水量时间序列的 t统计量在 1954—1985年超过了信度α=0.001的显著性水平，1985年的t统计量达到极大值且超过了信度α=0.001的显著性水平，表明太原盆地井灌区年降水量在1985年前后存在明显的突变现象。

表2 1954—2006年降水量滑动t检验结果

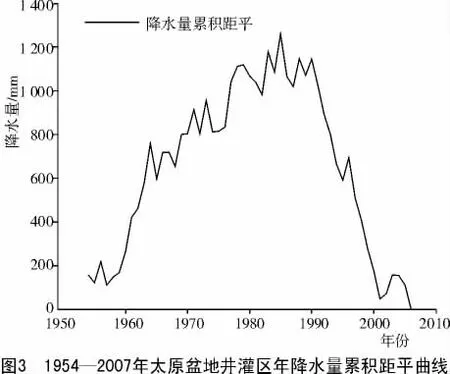
图3为太原盆地井灌区年降水量累积距平曲线，从图3可以看出，井灌区年降水量在1985年以后持续减少，即从1985年以前为井灌区年降水量正距平占优势的偏多阶段，转变为1985年以后年降水量负距平占优势的偏少阶段[5]。

2.3 灰色系统的引入和模型的建立

影响降水量的因素是纷繁复杂的，不是用几个指标所能表达清楚的。而且这些因素之间的结构关系难以准确描述，它们对降水量的作用也无法精确计算。这反映了降水系统是一个既含有许多已知信息，又存在许多未知或未确知信息的灰色系统[6-8]。对灰色量进行预测，是从自身的时间序列中寻找有用信息建立模型，发现和认识内在规律并进行预测。但不是说，像降水这样的灰色量不受任何因素的影响，实际上其所受的影响，已或多或少地反映在起伏波动的数据里。正是这些既明白又不完全清楚的众多因素共同作用的结果，才获得了现实的一个灰色量——年降水量[9]。

某个地区的降水情况是一个综合、复杂的不确定系统。通过对灰色量用一定的方法处理，建立动态模型，可将原始数据的随机性弱化，减少原来的不规律性和干扰性，使分析预测的整体趋势逼近实际。所以我们可以把某个地区的降水情况作为一个灰色系统进行研究[10-12]。

2.3.1 灰色系统GM（1，1）降水量分解模型通过观察不同时段的降水量数据，发现该数据序列同时存在着几种不同的趋势量，大致可以分为3个组成部分，即降水量的长期趋势量~x（0）（t）、周期波动量E（ti）以及随机变化量R（t）。运用灰色系统 GM（1，1）模型模拟降水量的趋势量~x（0）（t），通过对GM（1，1）模型残差的周期分析获得周期波动量E（ti），合并趋势量与周期波动量得到降水量的周期修正量，然后通过对周期修正量的残差分析获得随机变化量R（t）。合并趋势量~x（0）（t）、周期波动量E（ti）和随机变化量R（t），得到降水量的变化过程，这种方法被称为灰色系统GM（1，1）分解模型[13]。

2.3.2 降水量的趋势量利用GM（1，1）模型分析降水量的总趋势，首先要对原始的数据序列x（0）（t）作一次累加生成后，形成一条单调增长序列 x（1）（t），它弱化了数据列的随机性，增加了规律性，然后再建立微分方程。该模型的一阶微分方程为：

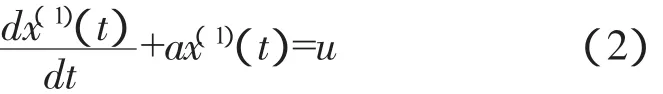
其中，x（0）（t）代表研究年 t的降水量；x（1）（t）为 x（0）（t）的逐年累加值，即t=1，2，……，n；a为系统的发展系数；u 为灰色作用量。求解微分方程（2）得到时间函数：

对方程（3）再进行累减还原，得到：

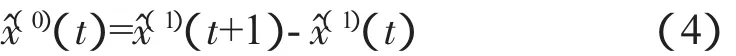
方程（3）和（4）即为 GM（1，1）模型进行灰色预测的基本计算公式。x＾（0）（t）即为运用 GM（1，1）模拟得出的降水量的趋势量。

2.3.3 降水量的周期波动量降水量的周期波动量要通过对GM（1，1）残差周期分析获得，对GM（1，1）模型的残差序列依次分段用相应周期长度与变幅的正弦（或余弦）曲线去拟合残差序列，计算公式为：

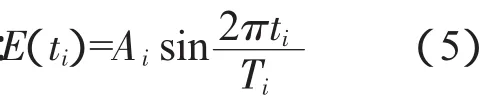
式中，E（ti）为第i个周期t年的残差拟合值；Ai为第i周期的最大变幅；Ti为第i周期的长度[14]。降水量周期可根据残差序列而确定，对残差序列拟合最好的正弦（或余弦）曲线的周期即为降水量的波动周期。

最后将计算得到的各个残差拟合值分别叠加到同一时刻GM（1，1）模型的趋势量上，即：

2.3.4 降水量的随机波动量降水量的随机波动量可以通过公式计算，即：

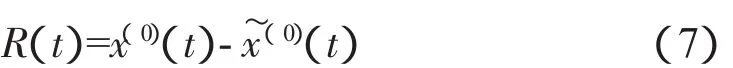
合并趋势量、周期波动量和随机变化量，可获得降水量的变化过程。由于随机波动的不可预测性，实际计算时用其绝对平均值来代替。

式中，Q（t）为模拟的降水量；其余符号同公式（4），（6），（7）。

2.4 降水量的计算与预测

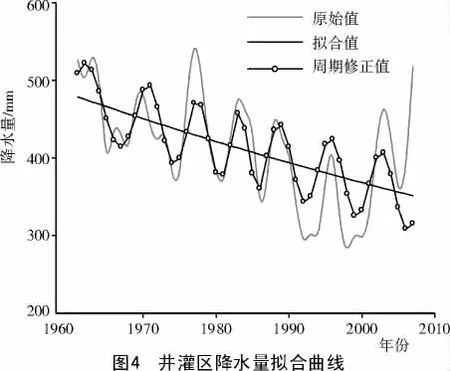
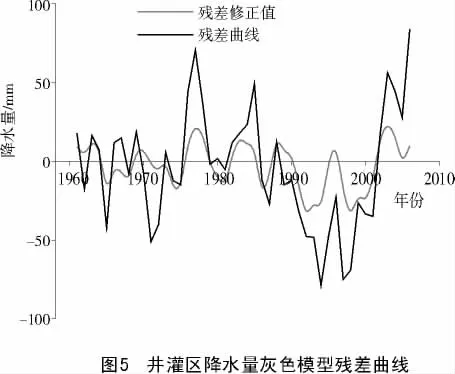
以太原盆地井灌区1960—2007年降水量作为原始序列建立GM（1，1）模型，求得系统参数为a=0.006 728 575，u=483.726 6，预测模型为1）（t+1）=-71 366.5e-0.006728575t+71 891.4。其中（＾t）为时间函数；e为自然函数的底，e=2.718 282；t为时间自变量。GM（1，1）拟合曲线与降水量的拟合情况如图4所示[3]。对GM（1，1）的残差序列作出曲线（图5中残差曲线），此时的残差绝对平均值为=46.613 05，平均相对误差为12.094 83。根据残差曲线可知，残差序列的周期为 T1=9，T2=7，T3=5，T4=5，T5=7，T6=7，T7=7，函数类型为正弦。为了方便计算，取残差绝对平均值为变幅=46.613 05，逐点求出修正值，再叠加到原模型计算值上，形成修正曲线，修正曲线与原始数据的拟合情况如图4所示。修正后的残差序列作出曲线如图5所示的残差修正值。经残差周期修正后，残差绝对平均值为33.437 1，平均相对误差为=8.477202。模型精度有明显提高。

根据对太原盆地井灌区降水变化趋势和特征的研究，结合上述模型的计算结果，确定太原盆地井灌区降水量变化周期T=7。在进行预测时，预测周期T=7，变幅A=100，将T，A值代入公式（6），对2010—2020年的降水量进行预测，结果列于表3。

表3 2010—2020年降水量预测结果 mm

3 结论

太原盆地中部农业井灌区54年来降水量呈减少趋势，年内平均降水量71.23%集中在6—9月份，12—2月降水量最少，占1.49%，降水量明显集中于夏季。1954—2007年描述性统计结果表明，各月降水量变异系数较大，降水量波动明显，12，1，2月份属于强变异性。以11年为基准，把近54年年降水量数据分成5段数列计算平均值，从分段的结果来看，降水量也呈现出明显的减少趋势，1987—1997年段的降水量平均值最小，1954—1964年段的降水量平均值最大。

采用滑动的t检验法，对近54年的降水量进行突变分析检验，结果表明，研究区降水量在1985年前后存在明显的突变，1985年的t统计量达到极大值，且超过了信度α=0.001的显著性水平，结果与图1-B反映的情况吻合，在1985年后的1987—1997，1998—2007年 2个年份段降水量较 1954—1964，1965—1975，1976—1986年3个年份段降水量有明显的突变减少。结合图3，降水量的累积距平从1985年以前为年降水量正距平占优势的阶段，转变为1985年以后年降水量负距平占优势的阶段。

在分析太原盆地井灌区54年的降水量特征的基础上，用灰色模型对降水量进行预测，得到GM（1，1）的残差序列值，残差绝对平均值46.613 05，平均相对误差=12.094 83，经残差周期修正后，残差绝对平均值=33.437 1，平均相对误差|q（t）|=8.477 202，模型精度有明显提高。从预测值可以看出，2013，2014，2015年为枯水年，2010，2011，2018年为相对丰水年。根据预测结果要做好相应的工作，在太原盆地井灌区采取科学种植，节约用水，最大限度保护水资源，采取积极措施建立长效的节水农业发展机制[16]。

从实例中总结出灰色预测模型与一般的时间序列分析、回归分析建立的预测模型不同，它不需大量的原始数据，具有计算量小、计算方便和预测精度高等诸多优点，但在实际中，需要不断地将新测得的降水量值加到原始序列中，以便对原始数据序列进行调整和更新，从而使预测结果更加准确。

［1］边红娟，雷宏军，王勇，等.灰色理论在区域降雨量预测中的应用——以河南商城县为例[J].安徽农业科学，2009，37（13）：6059-6060.

［2］王学萌，郝永红.中国总人口的灰色动态预测[J].中国人口资源与环境，2001，11（S2）：100-102.

［3］郝永红，黄登宇，张文忠，等.山西神头泉流量的灰色预测模型研究[J].水利学报，2004（2）：112-114.

［4］符淙斌，王强.气候突变的定义和检测方法[J].大气科学，1992，16（4）：483-492.

［5］张智，林莉，孙银川，等.银川市日照时数气候变化特征分析[J].干旱区研究，2006，23（6）：345-348.

［6］王学萌.灰色系统分析及实用计算程序[M].武汉：华中科技大学出版社，2001.

［7］王学萌，聂宏声，李晋陵，等.灰色系统模型在农村经济中的应用[M].武汉：华中理工大学出版社，1991.

［8］常春华，熊黑钢，鲁魁锋.基于灰色系统模型的新疆奇台县农业供需水量预测及其平衡分析[J].山西农业科学，2010，38（5）：24-27.

［9］郝永红，黄登宇，张文忠，等.GM（1，1）的周期修正模型及其在泉水流量预测中的应用[J].数学的实践与认识，2003，33（13）：36-37.

［10］刘思峰，党耀国，方志耕，等.灰色系统理论及其应用[M].北京：科学出版社，2007.

［11］王学萌，聂宏声，李晋陵.灰色系统模型在农村经济中的应用[M].武汉：华中理工大学出版社，1989.