一种快速扩展视野超声成像方法研究

苏立楠 高上凯

(清华大学医学院生物医学工程系，北京 100084)

一种快速扩展视野超声成像方法研究

苏立楠 高上凯*

(清华大学医学院生物医学工程系，北京 100084)

传统超声检查中由于探头宽度或发射波束角度的限制，会导致成像视野受限，使医生无法全面了解被成像部位组织的结构特征，而扩展视野成像方法可以很好的解决这一问题。本研究改进了现有的多模块匹配技术，以提高模块匹配过程中的抗噪能力;利用变步长搜索方法极大缩短了搜索过程;优化了求解变换矩阵和图像拼接过程，提出了一种更有效的权重系数评估方法，使算法更具鲁棒性和实用性。为了验证算法的有效性，首先利用该算法对体模扫描图像进行拼接实验研究，证明该算法在扩展视野成像上应用的可行性以及良好的拼接精度;然后通过对肌腱和甲状腺等组织超声图像的研究表明，该方法不仅具有良好的成像效果，而且运算量较小，有可能实现实时成像。

扩展视野超声成像;图像配准;图像拼接;块匹配算法

引言

超声成像具有实时、无创等优点，被广泛的应用于各类临床检查当中。但是常规超声在对肝脏，甲状腺，肌腱等器官成像时往往受到探头宽度和波束角度限制，导致图像视野局限于较小范围内。为了扩展扫描区域，医生需要反复移动探头，但是局部成像仍然不能直接反映出器官的整体结构，目前已经成功开发的扩展视野成像技术可以很好地弥补这个缺陷。

扩展视野成像也被称为宽视野成像或者全景成像，类似技术已经在照片处理、虚拟现实［1］、卫星图像合成［2］等方面有很多应用，但超声图像由于其分辨率低、噪声大且要求实时成像等特点，使得超声扩展视野成像方法与前面提到的技术有所区别。

扩展视野成像从实现技术上看可以分为两类，第一类是通过安装在探头上的位置传感器对探头进行空间定位［3］，再利用定位信息对图像进行拼接，但是这样的系统成本较高，而且有些传感器容易受到外界干扰，造成定位不准［4］;第二类是利用超声图像序列间的相似性，基于图像内部特征进行匹配，实现扩展视野成像［4－6］。

目前比较成熟的扩展视野成像方法是基于多模块匹配技术的［4－6］。此项技术是在一帧图像中的不同位置选择多个模块进行搜索匹配，由此计算得到整体图像移动的结果，采用该方法得到的匹配结果具有较好的稳定性，但是搜索过程计算量较大，实时计算负担较重。此外，上述方法对模块匹配误差的评估方法较为单一，容易造成结果的失真。本研究在借鉴参考文献［4］的基础上，改进了现有的匹配方法和权重评价规则，提高了计算结果的准确性;同时本研究还通过加速匹配和求解过程的方法，有效的缩短了计算时间。本研究重点研究处理方法，所展示的是基于已经获得的超声序列图像，利用Matlab程序进行离线分析处理的结果。经过初步验证，本研究提出的方法在计算精度上可以满足要求，并且有望进行实时计算。

1 扩展视野超声成像原理及方法

1.1 数学模型

当超声探头在探查目标上缓慢移动时，将获得序列超声图像。定义这些图像的坐标原点都在图像的左上角，横轴为 x，纵轴为y。因为相邻两帧之间的相对位移实际很小，有大量重合区域，因此可以假设序列图像全部处于同一平面内，而且连续两帧图像的重合区域之间只存在刚性变换，即只有平移和旋转。于是，连续两帧图像坐标系之间的变换关系可以用数学方程表达［7］，即

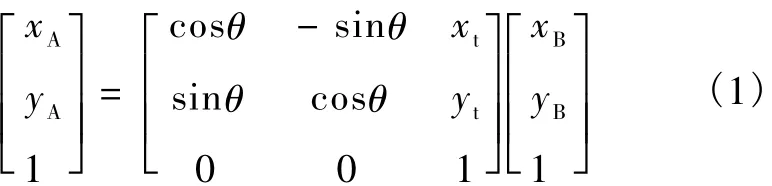
式中，(xA，yA)和(xB，yB)分别表示某一特定像素点在图像A和图像B下所对应的坐标。θ表示两幅图像之间的旋转角度，顺时针方向为正，逆时针为负;(xt，yt)表示图像 B相对于图像 A的平移量。本研究的扩展视野成像方法的基本数学模型就是求解方程(1)中的旋转角度 θ和平移量(xt，yt)，进而利用变换方程完成图像拼接工作。实际上，假定图像B中某个点(xB，yB)在图像A中对应的坐标为 (xA，yA)，这样的对应点对必然满足方程(1)，如果得到若干组这样的点对，就可以求解出变换矩阵。

1.2 基本数据处理流程

数据获取和处理流程如图1所示。由于本研究的算法是基于已经采集的序列图像进行的，因此准备拼接的序列图像被集中存放，拼接时再逐帧读出进行处理。具体拼接过程如下:

(1)图像预处理:由于获取的超声图像不一定能满足扩展视野要求，本研究首先对读取的图像进行预处理，将图像中有效部分裁剪为矩形，并且针对图像质量的评估进行筛选，如果当前帧图像相对前一帧图像产生突变(例如图像突然变黑等)，则将当前帧放弃。

(2)模块匹配:在当前帧图像中选择合适大小和数量的模块。匹配过程是将所有模块在前一帧图像中对应区域内进行搜索，而且假设在搜索区域内模块只存在平移运动，在找到相似度最大的位置后，将模块中心的位移视为当前帧图像的局部位移。

(3)变换方程求解:对当前帧图像所有模块匹配结果进行分析，并给每个模块赋予相应的权重，剔除明显匹配错误的结果。利用当前帧图像中所有局部位移及各个向量的权重拟合出该图像相对于前一帧图像的变换方程，即求解出方程(1)中的旋转角度θ和平移量(xt，yt)。

(4)图像拼接:如果认为当前帧适合拼接，则利用方程(1)将当前帧拼接到目标图像上，并且将结果显示、存储，返回图像存储区重复执行上述过程;如果认为不适合拼接，则直接返回存储区重复上述过程。

图1 数据处理流程图Fig.1 Diagram of data processing

1.3 算法实现

从上述流程可以看出，多模块匹配方法的主要计算包括模块匹配(Block-matching)、求解变换矩阵和拼接图像三个过程，本研究的主要研究目的在于在保证扩展视野成像质量的前提下，尽可能减少上述过程的计算时间。

模块匹配结果的准确性是决定最终结果的重要因素，所以需要选择合适大小和数量的模块，模块过大会造成计算量增大，过小则会导致包含信息量不足，匹配误差增大［4］。根据文献［4］给出的经验值和实验研究，模块大小一般选择为32像素×32像素，考虑到匹配误差等因素，模块数量通常选择在10～20块之间，如图2(a)所示。模块位置选择在图像的中上部，目的是在模块中包含较多的信息，减小匹配误差。

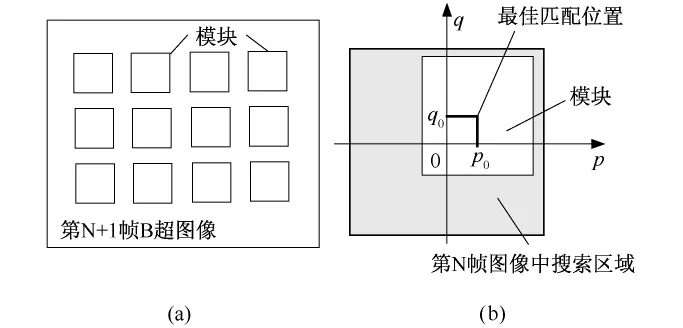
图2 模块选取与匹配示意。(a)模块选取;(b)模块匹配Fig.2 Block selections and block-matching.(a)block selections in ultrasound image;(b)block-matching

模块匹配方法的基本原理是在搜索区域内找到与模块相似度最高的位置，相似度可以有很多种定义，例如利用明氏(Minkowski)测度距离，相关系数等［9］。明氏测度距离定义方法较为直接，特别是一阶明氏测度距离，即图像间灰度差绝对值之和(Sum of Absolute Differences，SAD)［6］计算最为简单。如图2(b)所示，以第N+1帧图像中模块中心点在第N帧图像中的位置为原点建立搜索区域坐标系(p，q)，在第N帧图像中移动模块向四周进行搜索，则搜索区域可以是一个矩形。SAD算法计算公式为:

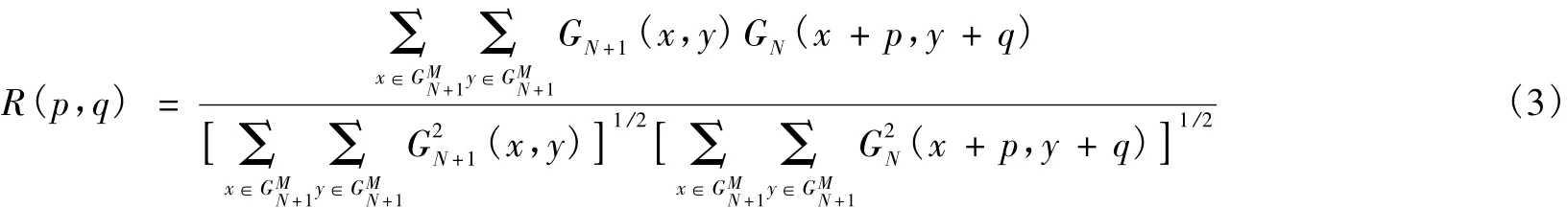
公式中参数与SAD算法定义相同，匹配条件可以描述为:当 R(p，q)≤R(p0，q0)时，认为(p0，q0)为与模块最为匹配区域的中心，即模块中心位移。在下文讨论中，R(p，q)被称为匹配值或NPROD匹配值。

可以看出，归一化积相关方法比SAD方法的计算量略大，为了具体比较两种方法的差异，利用Lena图像进行仿真研究。Lena图像为512像素×512像素灰度图像，取左505列加入白噪作为第N帧图像(图3(a))，取右505列加入白噪作为第N+1帧图像(图3(b)、图3(c))，相当于相邻两帧图像水平位移7个像素。利用PC平台(CPU:Intel core E6300双核1.86GHz，2G内存，Matlab 7.5。下文中如没有特别说明，所有数据均是在此PC平台下计算获得。)研究比较两种方法的计算时间和计算准确度。

图3(b)为采用SAD方法得到的结果，在左上区域匹配出现较大误差;图3(c)为采用NPROD方法得到的结果，可以看出NPROD方法稳定性好于SAD方法。另外SAD法一次匹配平均耗时为37 ms，而NPROD方法一次匹配平均耗时为44 ms，说明在目前PC平台下，两种方法耗时基本在同一水平上，而 NPROD方法在低信噪比图像中效果更好［9］，故采用NPROD算法是更合适的。

图3 SAD方法与NPROD方法匹配结果对比。(a)第N帧图像;(b)第N+1帧图像采用SAD方法模块匹配结果，(c)NPROD方法匹配结果Fig.3 Comparison of the block-matching results with SAD method and NPROD method.(a)image of frame N;(b)block-matching results with SAD method;(c)block-matching results with NPROD method

模块匹配最为直接的方法就是将整个搜索区域进行遍历搜索(Full Search Algorithm，FSA)［10］，可以看出，搜索区域大小直接影响匹配过程的计算时间。如图2(b)所示，为了确保搜索的准确性，通常横向搜索区域为－16～16，纵向搜索区域为 －16～16，进行遍历搜索时匹配次数将达到1 089次。观察超声图像序列匹配结果发现，遍历搜索实际上是按照步长为1的方式进行搜索，效率较低，而且每两步之间存在大量重复计算，因此可以采用变步长方式进行加速搜索。变步长搜索方法有很多，例如三步搜索 法 (three step search，TSS)［10］、交叉 搜 索 法(cross search algorithm， CSA)［11］、菱 形 搜 索 法(diamond search，DS)［12］等，目的都是在基本不影响匹配准确性的前提下，尽量加快匹配过程。比较多种变步长搜索方法，发现三步搜索法稳定性较高，计算量适中。三步匹配法具体实施过程如图4所示。假设从原点开始各个方向上最大搜索距离为d(图4中 d=8)，第一步以原点为中心点，对中心点和距离中心点横向/纵向距离为 d/2的9个位置进行搜索，如图4(a)，找到匹配值最大点;第二步以匹配值最大点为中心，将搜索范围缩短为d/4，搜索新的9个位置中匹配值最大点，如图4(b);直到搜索范围减到1，完成整个搜索过程，如图 4(c)。从上述搜索过程可以看出，对该区域进行遍历搜索，匹配计算次数将达到(2d+1)2次，而三步搜索法匹配计算次数仅为1+8log2d次，计算量明显减少了。而且通过实验验证，三步搜索法匹配较为准确，基本可以替代遍历搜索方法。

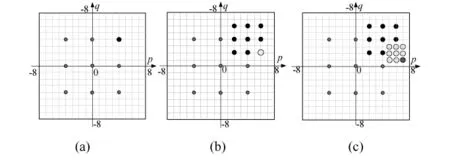
图4 三步搜索法搜索过程，搜索范围d=8。(a)第一步搜索，搜索步长为4;(b)第二步搜索，搜索步长为2;(c)第三步搜索，搜索步长为1Fig.4 Procedure of three step search，Search area，d=8，(a)the first step，the search distance is four;(b)the second step，the search distance is two;(c)the third step，the search distance is one

由于噪声等因素，匹配搜索很可能存在误差，为此需要对每个向量赋予一定的权重，如果认为模块匹配准确度较高，则赋予较高权重;反之给予较低权重或者直接剔除［5－6］。每个模块赋予权重的大小应该从多方面进行分析，不仅要考察该模块的匹配过程可信度，还要参考所有模块整体匹配结果。

在搜索区域中，如果在最佳匹配位置上的匹配值明显大于其他位置，则可以认为搜索过程可信度较高，应该对匹配结果赋予较高权重;反之，如果匹配值在最佳位置和其他位置差别不大，则认为匹配过程可信度较低，赋予较小权重。如图5(a)和5(b)所示，取相邻两帧肌腱部位超声图像，记为第N帧和第N+1帧，采用NPROD法将模块在搜索区域进行遍历搜索，将匹配结果与搜索位置对应画图如图5(c)。若匹配值中最大为 max(R)，最小为 min(R)，所有结果平均值为mean(R)，则可以定义该模块在搜索区域搜索结果的可信度w1为

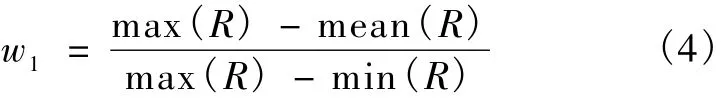
变步长匹配方法相当于对遍历搜索匹配结果进行了抽样，可以采用同样的方式进行权重计算。

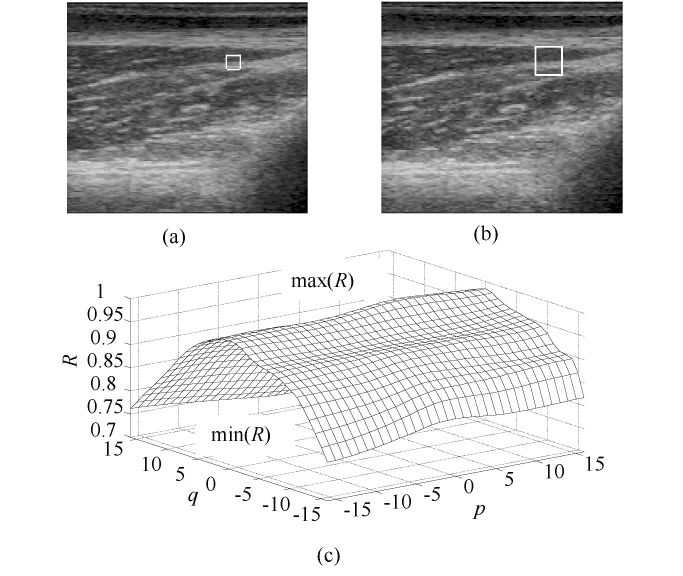
图5 模块遍历搜索结果示意。(a)第N+1帧图像及某个模块;(b)第N帧图像及该模块的搜索区域;(c)模块在搜索区域各个位置匹配结果Fig.5 Block-matching result with FullSearch Algorithm(a)one block in the image of frame N+1;(b)the block-matching area in the image of frame N;(c)block-matching results in the whole area

权重w1只能给出某个模块在匹配过程中的可信程度，但是对所有模块构成的整体运动情况考虑不足。实验观察发现，在超声设备帧频足够高，探头运动较为平缓的情况下，同一行的模块位移基本相同。假设某一行几个模块位移向量大小的均值为¯M，标准差为S，当S较大时，说明该行各模块间位移差别较大，如果该行上某个模块位移量大小M在之外，则被认为位移向量偏差较大，赋予较低权重，反之赋予较高权重。为了方便计算，对权重赋值采用二值化方法，即模块位移大小在之外权重赋值为0，其他权重为1，则该模块的位移可信度定义为w2为

同时考虑该模块的两次权重，最终权重定义为

将多个模块匹配得到的对应点对和权重代入变换方程(1)中，可以利用加权最小二乘法求解出变换矩阵。方程(1)属于非线性方程，需要进行迭代求解，迭代次数也是影响整个算法计算速度的重要因素。首先对所有模块匹配结果进行分析，可以判断大致的运动过程。当判断两帧为平移运动时，可以认为θ=0°，则式(1)转换为式(7)，式(7)为线性方程，求解过程计算量大为减少。当判断两帧之间存在旋转运动时，则仍然进行迭代求解。这种初步判断可以在基本不影响结果的前提下，加快方程求解速度。

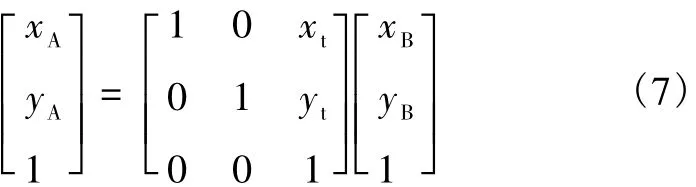
根据方程(1)得到第N+1帧到第N帧的坐标变换方程，再由递推关系可以确定所有图像之间的变换方程。当变换方程确定后，开始进行图像拼接。如前文所述，相邻两帧图像间通常具有很大的相似性，如果每帧图像都进行拼接，会严重耗费时间，所以需要设定拼接阈值，即当两帧之间相对位移大于一定长度时，开始进行拼接，否则丢弃当前帧图像。拼接阈值设定要适当，不宜过大，否则会导致一次拼接工作量过大，严重影响拼接速度，而且可能出现图像裂缝。另外，还需要选择合适的拼接方法，图像增长(image growing)［13］是一种耗费时间较少的方法，同时为了保证图像之间的“无缝连接”，需要利用双线型插值和加权拼接［3，13］。

2 扩展视野成像实验设计

为了研究拼接结果的准确性，首先对体模图像进行扩展视野成像。如图6(a)所示，体模中有若干固定间隔的靶线组，获得的超声序列图像如图6(b)所示，可以从该图像中看到明显的纵向靶线。利用该图像中纵向靶线可以确定1cm距离在图像中对应的像素距离，再根据这个距离衡量拼接后图像中各组靶线的间距判断拼接误差。最后利用该方法对甲状腺和肌腱图像进行扩展视野成像。

实验数据由汕头市超声仪器研究所有限公司提供。机器型号:CTS-8800，线阵探头L7L38G，中心频率7.5 MHz。体模(如图6(a))图像247帧，预处理后图像为248像素×472像素(图6(b));体模中含有间隔为1 cm的纵向排列靶线，间隔为1、2、3、4、20 mm的横向排列靶线;肌腱扫描图像150帧，帧频为25帧/s，处理后图像尺寸为545像素 ×477像素;甲状腺扫描图像120帧，帧频为25帧/s，处理后图像尺寸为362像素×472像素。实验采用Matlab 7.5进行离线分析处理。

图6 体模扩展视野成像。(a)体模结构示意;(b)含有纵向靶线超声图像;(c)扩展视野成像结果Fig.6 EFOV experiment on phantom.(a)phantom with marker lines;(b)phantom image with vertical marker lines; (c) compounded image with EFOV algorithm

3 实验结果

3.1 体模扩展视野成像

找到图6(b)中较为清晰的6根靶线，计算相邻两根之间距离，得到1 cm对应长度为68个像素，测量拼接后图像(图6(c))中横向靶线间距如表1所示，从表中可以看出，水平方向上形变较小，保证了扩展视野成像的准确性［14－15］。

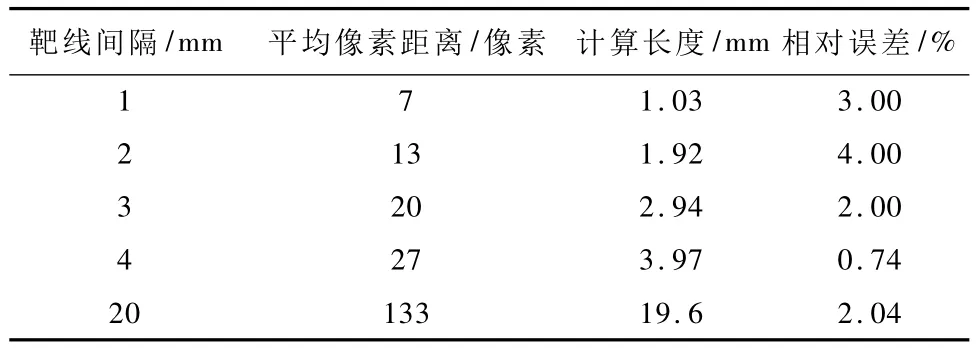
表1 体模扩展视野成像结果中横向靶线间距及误差Tab.1 Distance and error of horizontal marker lines in phantom EFOV image

3.2 肌腱和甲状腺的扩展视野成像

分别对肌腱和甲状腺图像进行扩展视野成像的结果如图7所示，图像特征与人体组织结构相符，图形畸变小，图像纹理清晰。

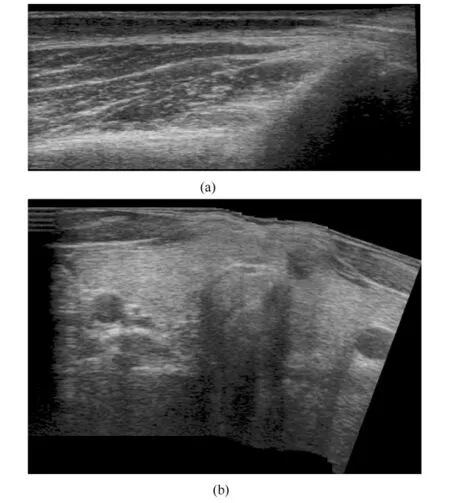
图7 肌腱与甲状腺扩展视野成像结果。(a)肌腱部位扩展视野成像;(b)甲状腺扩展视野成像Fig.7 EFOV images of tendon and thyroid.(a)EFOV image of tendon;(b)EFOV image of thyroid

3.3 计算时间统计

表2列出了利用本方法对体模，肌腱和甲状腺图像进行扩展视野成像过程的计算时间。可以看到，在图像大小合适情况下，拼接两帧图像时间基本上在500 ms以内。如果将该算法移植到执行效率更高的软件平台，完全有实现实时成像的可能。

表2 扩展视野成像过程耗时统计Tab.2 EFOV algorithm time cost of each step

4 讨论和结论

本研究所述方法都是在假设B超图像序列之间为刚性变换的前提下进行的，即忽略由于探头挤压、组织内部运动等原因导致的图像形变。刚性假设的优势在于匹配过程简单，而且对于大多数图像的扩展拼接具有相当高的准确性，但是如果组织形变较大，则必然造成匹配的不准确。仿射变换［8］可能是解决问题的手段之一。但是实验中发现，仿射变换很难准确地找到两帧图像之间的关键匹配位置，匹配位置误差会直接导致拼接过程中误差累计，拼接后图像会产生明显不符合组织结构的畸变。

可以看到，利用所述方法进行扩展视野成像，图像配准过程具有较高的稳定性和鲁棒性，体模和组织成像实验表明拼接结果较为准确，图像畸变小，图像过度平滑，纹理特征明显，具有一定的应用价值。而且从处理过程消耗的时间可以看出，该方法已经具备了较好的实时处理能力，完全可以在C++等平台下实现实时成像功能。

(致谢:感谢汕头市超声仪器研究所有限公司为本研究提供研究数据)

［1］ 赵向阳，杜利民.一种全自动稳健的图像拼接融合算法［J］.中国图像图形学报，2004，9(4):417－422.

［2］ 孔延梅.用于微型卫星的空间遥感全景成像系统［J］.光机电信息，2009，26(4):18－23.

［3］ Prager RW，Gee A，Berman L.Stradx:real-time acquisition and visualization of freehand three-dimensional ultrasound［J］.Medical Image Analysis，1999，3(2):129－140.

［4］ Weng Lee，Tirumalai AP，Lowery CM，et al.US Extended-Field-of-View imaging technology［J］.Radiology，1997，203(3):877－880.

［5］ Weng Lee，Tirumalai AP.Method and apparatus for generating large compound ultrasound image［P］.United States Patent:5575286，1996－09－19.

［6］ 邵斌，唐娉，曾庆业，等.基于PC的实时超声全景成像系统中的图像配准［J］.计算机工程与应用，2007，43(28):206－209.

［7］ Hearn D，Baker MP，著，蔡士杰，吴春镕，孙正兴，等译.计算机图形学［M］.(第二版)北京:电子工业出版社，2002.162－163.

［8］ 江和平.红外序列图像匹配跟踪技术研究［D］.长沙:国防科学技术大学.2006.

［9］ 刘宝生，闫莉萍，周东华.几种经典相似性度量的比较研究［J］.计算机应用研究，2006，11:1－3.

［10］ Ghanbari M.The Cross-search algorithm for motion estimation［J］.IEEE Transactions on Communications，1990，38(7):950－953.

［11］ Jing Xuan，Chau LP.An efficient three-step search algorithm for block motion estimation［J］.IEEE Transactions on Multimedia，2004，6(3):435－438.

［12］ Zhu Shan，Ma Kai-Kuang.A new diamond search algorithm for fast block-matching motion estimation ［J］.IEEE Transactions on Image Processing，2000，9(2):287－290.

［13］ 李义兵，余大昆，林家瑞，等.实时全景超声成像技术.［J］.医疗设备信息，2005，20(10):39－40.

［14］ Kim SH，Choi BI，Kim KW，et al.Extended field-of-view sonography:advantages in abdominal applications. ［J］. J Ultrasound Med，2003，22:385－394.

［15］ Fornage BD，Atkinson EN，Nock LF，et al.US with extended field of view: phantom-tested accuracy of distance measurements.［J］.Radiology，2000，214:579-584.

Study on a Fast Extend Field of View Sonography

SU Li-Nan GAO Shang-Kai*
(Department of Biomedical Engineering，School of Medicine，Tsinghua University，Beijing 100084，China)

In the conventional ultrasound imaging system，image field of view is limited by probe width or probe scanning angle，which precludes doctors from getting full information about the observed region.The extend field-of-view(EFOV)techniques could solve the problem effectively.This research focused on developing a new method for block-matching to reduce the noise and decrease the time of computation.Moreover，the studies on solving the transform equation，images compounding and estimate blocks’weight were also presented in this paper.The feasibility of the algorithm was proved by the ultrasound images on phantom with the marker lines.The quantitative results showed the satisfactory accuracy.In addition，the EFOV experiment on thyroid and tendon ultrasound images showed that the algorithm could be applied for real-time EFOV imaging.

extended field-of-view(EFOV)sonography;image registration;image compound;block-matching algorithm

R318.08

A

0258-8021(2010)03-0373-06

10.3969/j.issn.0258-8021.2010.03.009

2009-11-20，

2010-01-22

*通讯作者。 E-mail:gsk-dea@tsinghua.edu.cn