基于分形的滑坡易发程度区划方法

李长江，麻土华，孙乐玲，李 炜，郑爱平

(1.浙江省国土资源厅信息中心，浙江 杭州 310007;2.浙江省国土资源厅地质环境处，浙江 杭州 310007;3.浙江大学地球科学系，浙江 杭州 310027)

基于分形的滑坡易发程度区划方法

李长江1，麻土华1，孙乐玲2，李 炜2，郑爱平3

(1.浙江省国土资源厅信息中心，浙江 杭州 310007;2.浙江省国土资源厅地质环境处，浙江 杭州 310007;3.浙江大学地球科学系，浙江 杭州 310027)

本文发展了一种基于分形统计的滑坡易发程度评价方法，该方法仅使用已有的滑坡数据，首先通过分形统计获得滑坡分布的分形丛集关系，再通过GIS的空间操作与分析生成滑坡易发程度区划图。提出一种对滑坡易发程度区划图的可信度和预测效果进行评价的方法。本文介绍了这些方法及其在浙江地区应用的结果。

滑坡;易发程度区划;分形;GIS

0 引言

滑坡是对公众生命和财产造成重大损失的主要自然灾害之一。通过对影响滑坡的地层岩性、断裂构造、地形地貌、植被土壤等环境因素的分析，进行滑坡易发程度分区和编图，用图示或者其它方法表示出滑坡易发区，简称滑坡易发程度区划。虽然这种方法对潜在的滑坡危险性只是提供一种静态的描述［1］，但是对于丘陵和山区的土地开发利用与管理决策却是一项必不可少的基础工作，在美国、意大利、德国、日本等国家称为编制滑坡敏感度图(landslide susceptibility map)。滑坡易发程度区划图的用途主要有二个方面:(1)使政府部门在制定区域的经济社会发展规划和环境保护规划时可以预先采取有针对性的减灾策略;(2)为重要工程建设选址提供依据，帮助建设规划者选择合适的场址，即使对潜在的滑坡危险区不能全部避免，也能够在规划的开始阶段就采取预防措施，最大限度地防止灾害。

可以使用许多不同的方法编制滑坡易发程度区划图，其中，最常用的是基于一般线性模型的统计学方法(如多元统计分析，唯一条件分析等)。近年来，许多研究使用各种统计学方法，在GIS平台上综合地形、地质、水文学和土地利用等多种参数(通常在5种以上)进行滑坡易发程度分析(如:Wadge，1988;Wang Shu-Quiang 和 Vnwin，1992;Pachauri 和 Pant，1992;Binaghi等，1998;Chung和 Fabbri，1999;Guzzetti等，1999;Lineback等，2001;Santacana等，2003;Lee 等，2007)［2-10］。此外，一些研究者采用基于物理学的方法分析有关斜坡的稳定性(如:Montgomery 和 Dietrich， 1994， Jibson 等，2000)［11-12］，但是这类方法依赖于斜坡物质的物理力学性质。然而，在世界许多地方，往往缺乏上面提到的这些数据或者可获取的数据难以满足现有方法的要求，但是又迫切需要编制滑坡易发程度区划图。面临的一个问题就是:能否从有限的数据获得可靠的滑坡易发程度区划图?Coe等(2004)［13］曾以危地马拉东中部一个约900km2的地区为例探讨了仅使用高程和坡度两个参数评价滑坡易发程度的方法。

另一方面，在编制的滑坡易发程度区划图提供使用之前，必须对它的可信度和预测效果进行检验，然而国内的研究报导通常只论述编图方法和结果，鲜有涉及对结果的检验。目前国际上也尚无一个能够被普遍接受的评价标准。

我们发展了一种基于分形统计的滑坡易发程度评价方法，该方法仅使用已知的滑坡数据，首先通过分形统计获得滑坡分布的分形丛集关系，再通过GIS的空间操作与分析生成滑坡易发程度图。提出了一种对滑坡易发程度区划图的可信度和预测效果进行检验的方法。本文介绍了这些方法及其在浙江地区应用的结果。

1 方法

一群点与其它点有着极为邻近的联系，称为丛集，丛集的度量是一个点事件发生在时间或空间间隔中的概率。分形丛集分布与随机分布和均匀分布的区别(图1)。对于随机分布，所有事件的发生完全是不相关的，而具自相似性的分形丛集分布，在自相似性存在的范围(无标度区)内，所有事件之间是有某种相互关联的。

这里应用 Mandelbrot(1985)［14］推广的数盒子法(box-counting method)考察滑坡在空间上的分形丛集分布。对已知的若干滑坡，在不考虑单个滑坡之间在体积和滑动面深度上的差异，即把滑坡视为空间上的一个点集时，将一个面积为L×L的研究区域划分成边长为r的若干正方形单元进行统计。通常是从数大格子开始，依次减小格子的尺度。当r不同时，分别统计出有滑坡的格子数N(r)，即只计算那些含滑坡的格子数。N(r)显然与r有关。对一系列的r计算N(r)，如果N(r)与r之间的关系满足

则说明这些滑坡在给定的r范围内遵循分形丛集分布或是自相似的。这里，D为分维数。对于自然现象，由式(1)定义的分形关系一般只能在一定的尺度(r)范围内成立，这个范围称为无标度区。通常的作法是以N(r)与r作双对数坐标图，其直线部分的斜率即为式(1)中的D。数盒子法的操作方法如图2所示。分形分准基平原理的详见文献［15-16］。

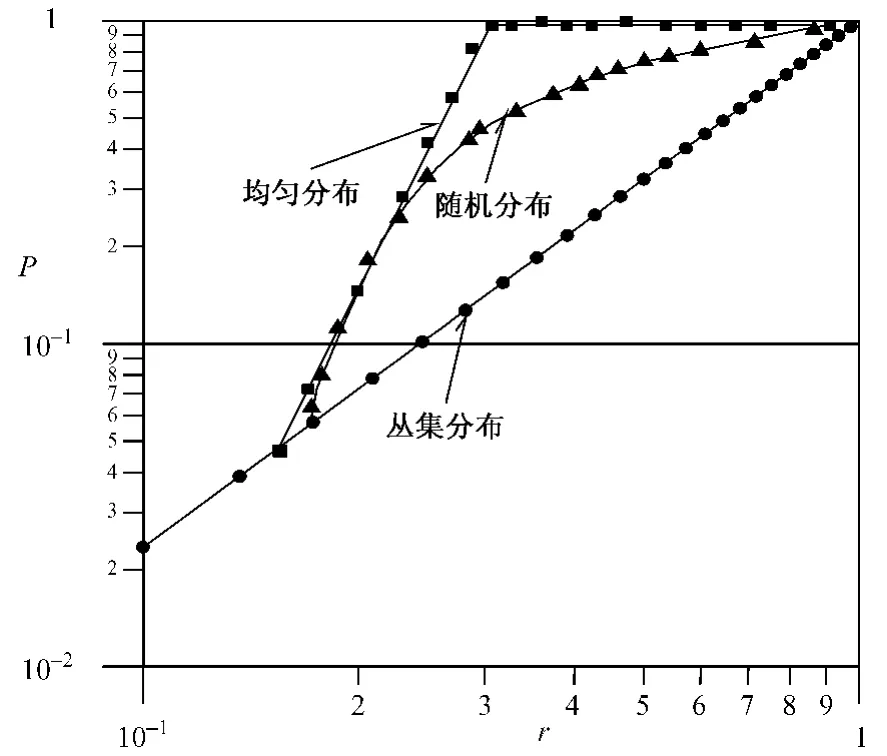
图1 分形丛集分布与随机分布和均匀分布对比示意图(纵坐标P表示事件在观察尺度r中出现的概率)Fig.1 Comparison of fractal clustering distribution with random and even distribution.(P on the Y-coordinate shows the probability that events occur in an observing scale with r.)

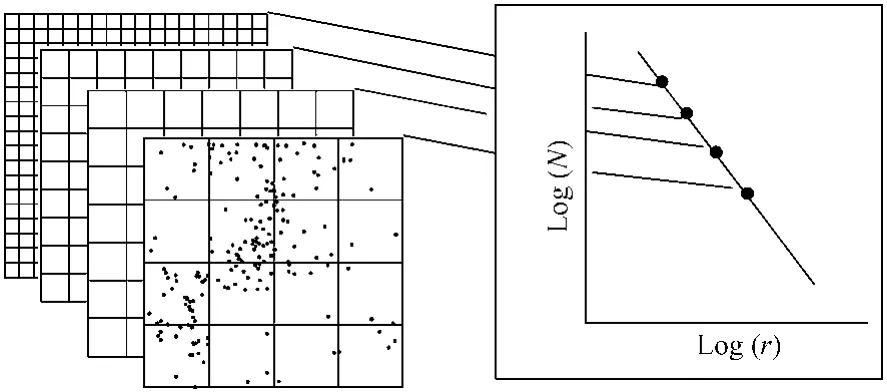
图2 计算分形维数的数盒子法图解。用边长为r的正方形网格覆盖研究区，当r变化时，将含有滑坡的格子数N(r)与格子边长r投在双对数坐标图上，通过对数据点拟合得到的直线的斜率求得分维数DFig.2 Schematic diagram illustrating the fractal box-counting method in which the study area is overlain by a grid of square cells or boxes and the number of boxes that contain one or more landslides is counted.The grid-box size is change and the counting procedure is repeated.The number of occupied grid boxesversusthegrid-box sizeis plotted on log-log axes.The points were best fit by a least-squares a straight line.The slope of thestraight line is the fractal dimension D.

作为对数盒子法应用的一个推广，让N(rmin)表示所取格子尺度最小时含有滑坡的格子数，在格子大小为ri时，含有滑坡的格子数N(ri)与N(rmin)的比率

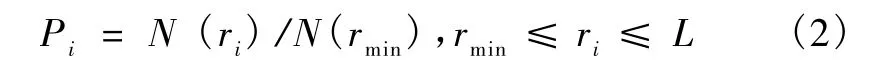
对一系列的r进行计算，得到P与r的关系为

P可以被理解为格子尺度为r时含有滑坡的概率。基于一个众所周知且被广泛接受的原理“过去和现在是打开将来之门的钥匙”，即过去和现在导致斜坡或沟谷不稳定的条件也是将来最可能引发滑坡的条件，在进行滑坡易发程度评价时，就可以应用式(3)对已经发生的滑坡的数据进行拟合，如果这些滑坡在空间上遵循分形丛集分布关系，就可以根据这个分形丛集分布关系对已知滑坡点周围不同距离内的滑坡概率进行评价。

2 应用

浙江位于中国东南沿海(图3)，陆域面积10.18×104km2。浙江地形复杂，地势高低悬殊。标高在300m以上的丘陵和山地约占全省面积的70.6%。整个地势由西南向东北倾斜，呈阶梯状下降。浙西南部地势高峻，大多为平均海拔800m以上的山区，最高海拔处1929m;中部以丘陵为主，大多为500m以下的低山丘陵，在丘陵山地之间分布一些盆地;东北部是低平的冲积平原，平均高程2～5m。

地层的分布大致以以北东向的江山─绍兴断裂为界，浙西北区除了少量火山岩层，花岗岩，以及分布在个别断(坳)陷盆地内的白垩纪红色碎屑岩以外，广泛发育元古代、古生代地层，沉积了巨厚的碎屑岩类夹碳酸盐岩。浙西北区地质构造复杂，断裂皱褶发育。浙东南则分布大片的中生火山岩，仅局部夹沉积岩，构造以断裂为主。在一些白垩纪断陷盆地发育红色粉砂岩、砂岩、砾岩等。少部分地区为第三纪玄武岩所覆盖。许多规模不等的中酸性岩体侵入于火山岩中。沿江山─绍兴断裂两侧局部出露有前寒武纪变质岩。

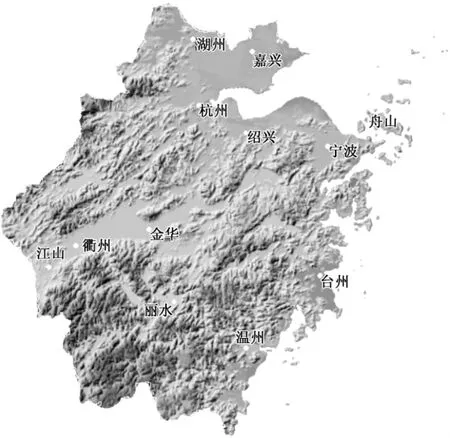
图3 浙江地势Fig.3 Topographic sketch in Zhejiang Province

地层岩石常被断裂切割，岩石的破碎程度以及风化层厚度等变化很大。几乎所有的斜坡都为厚度和组成变化很大的残(坡)积层所覆盖，属于滑坡易发地区。由于地理位置、地质和地形的原因，浙江每年都会遭受暴雨袭击，暴雨或强降雨往往引发大量浅层滑坡(主要为土体滑动和泥石流)。

从1969年至2007年12月，浙江全省有记载的滑坡总计4835处，在这些滑坡数据中，有发生位置(或坐标)记录的滑坡点总计3744处，其中，在1990～2003年发生的为3285个，2004～2007年发生的为459个。这些滑坡主要属于降雨引发的浅层滑坡。我们使用前一时间段的3285个滑坡编制滑坡易发程度区划图，以后一时间段的459个滑坡作为对滑坡易发程度区划图的检验样本。应用滑坡的分形丛集分布关系编制滑坡易发程度图的方法包括两个步骤。

首先使用式(3)对浙江在1990～至2003年期间发生的3285个滑坡进行统计，在计算中以1×1km的网格作为覆盖研究区的最小格子。采用最小二乘法对ln(r)和ln(P)进行拟合得到

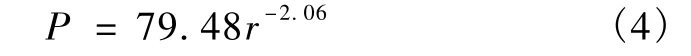
图4显示P与r之间的关系在1～15km范围内呈一条直线，表明这些滑坡在1～15km范围内并非彼此毫不相干的孤立事件，而是具有相互联系的分形丛集分布。

图4 浙江省在1990～2003年期间由降雨引发的3285个滑坡的分形丛集分布(图中横坐标r表示覆盖研究区的格子尺度，纵坐标P表示在格子尺度为r时含滑坡格子数占格子尺度为rmin时含滑坡格子数的比率)Fig.4 Variation in P with rfor 3285 landslides triggered by rainfall during the period 1990～2003，Zhejiang Province

然后，对3285个滑坡点形成一个滑坡分布图，利用GIS的Buffer(缓冲区)功能，根据式(4)，分别以每个滑坡为中心，以2～15km为半径作 Buffer分析(因为在间距小于或等于1km时为取作中心的滑坡点本身，无意义，故取半径为2～15km)。对所有已知滑坡点依次进行，这样可以形成一系列的对应于不同r的Buffer分区，分别记作 tmp-1，tmp-2，…，tmp-n。对各区取最大值 P(r)=max(tmp-2，tmp-3，…，tmp-n)，最后得到一个 P(r)分布图。对 P(r)图进行光滑处理(这里采用7×7的网格)后进行滑坡易发程度分区。OAS(1991)［17］曾使用一种 F 函数［18］对滑坡易发程度进行分区。一个5级的F函数(也可以根据划分等级的需要对F函数取3级或4级，等等)可以表示为

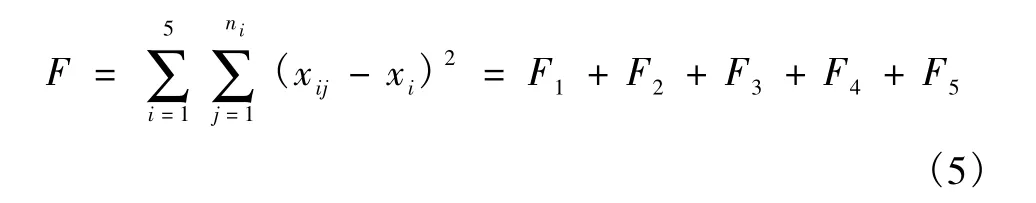
这里，x表示一组观察值［在本项研究中为P(r)］，xij为第 i组中第 j个值，ni是第 i组数据的个数，xi是i组内的平均值。只要取各组数据的F值为最小，那么此时的5组数据的分界即认为已确定。

使用式(5)对得到的P(r)值进行分区，得到5组数值从小到大依次为 1.18、1.27、1.30、1.36，1.47。以此作为界线值，将滑坡易发程度分为5个等级，即不易发区(Ⅰ)、低易发区(Ⅱ、中易发区(Ⅲ)、高易发区(Ⅳ)和极高易发区(V)。将这个结果通过GIS显示和输出就得到滑坡易发程度分区图(图5)。

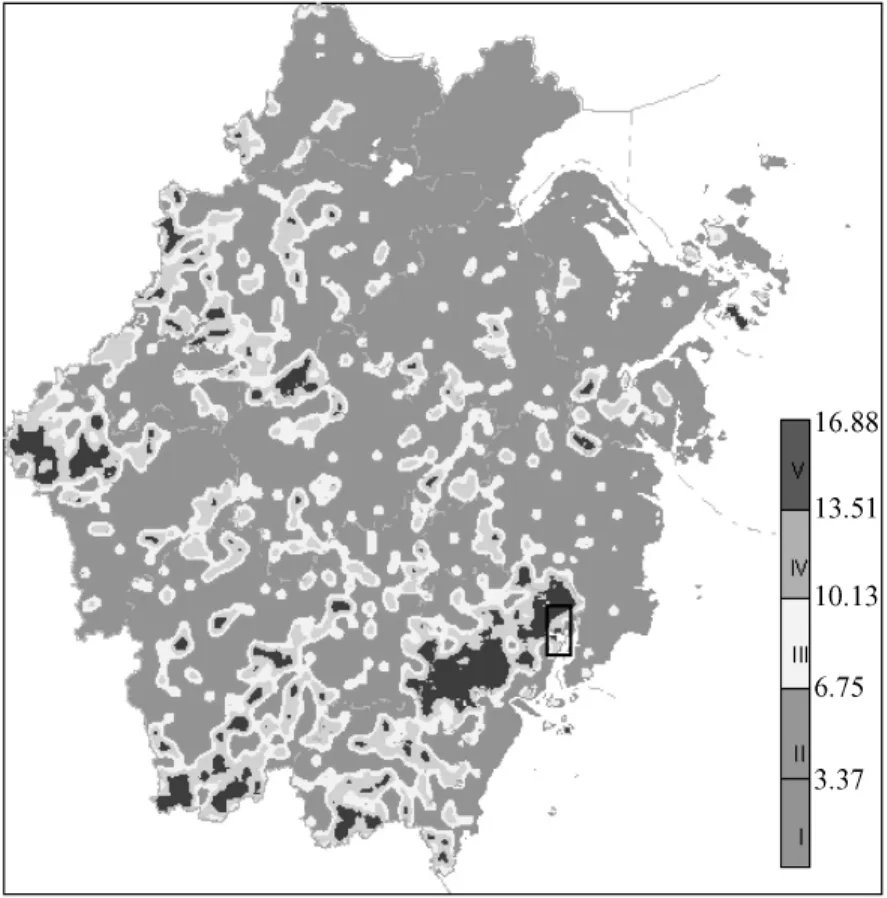
图5 由分形丛集统计方法使用1990～2003的期间由降雨引发的3285个滑坡编制的浙江省滑坡易发程度区划图(对图中黑色线框内区域按100×100m网格 编制的乐清市滑坡易发程度区划图见图7)Fig.5 Landslide susceptibility map of Zhejiang Province.The map is produced using the fractal clustering relations for the spatial distribution of 3285 landslidestriggered by rainfallduring the period 1990～2003.

3 对滑坡易发程度区划图的检验

一个地区的滑坡易发程度区划图编制完成，在提供使用前应当对它的可信度和预测效果进行评价。

对滑坡易发程度区划图的效果可以通过实际发生的滑坡来进行检验，并且作为检验用的滑坡点不应被包含在编制滑坡易发程度区划图时使用的滑坡数据中。对滑坡易发程度区划图的检验包括两个方面:(1)检验组样本落在滑坡高易发区的百分比和不易发区占整个工作区的面积百分比，滑坡易发程度编图应当使这两个值最大化;(2)考察检验组样本落在各等级区的百分比对各等级区的面积百分比的比值，对于一个合理的滑坡易发程度分区，从滑坡的不易发区到高易发区，这个比值应当是增大的。

基于上述两个检验准则，以 A(pi)表示第 i级区的面积占工作区总面积的百分比，L(pi)表示落在第i级区的滑坡占检验组滑坡总数的百分比，以L(pi)对A(pi)的比值，即

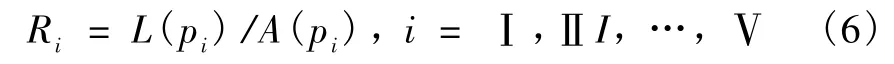
作为对滑坡易发程度分区的评价指数，该指数表征了滑坡活动的强度，如果

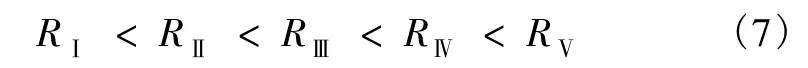
成立，则说明对滑坡易发程度的分区是合理的。

按照以上检验方法，在图5中，5类滑坡易发程度分区的面积占浙江陆地区域总面积的百分比分别为:不易发区(Ⅰ)52.01%、低易发区(Ⅱ)16.10%、中易发区(Ⅲ)16.66%、高易发区(Ⅳ)10.79%、极高易发区(V)4.44%。将2004～2007年发生的有坐标(位置)记录的459个滑坡点作为检验样本投在编制的滑坡易发程度图(图5)上进行检验，检验的结果表明，落在各区内的滑坡占检验组样本总数的百分比分别是:不易发区(Ⅰ)4.18%、低易发区(Ⅱ)2.0%、中易发区(Ⅲ)10.16%、高易发区(Ⅳ)47.54%、极高易发区(V)36.12%。其中，滑坡易发区(Ⅳ)和极高易发区(V)的面积占了研究区总面积的15.23%，但是落在这两个区的滑坡占了检验组滑坡总数的83.66%。这个检验的结果(表1)表明图5对滑坡易发程度的分区是合理的。

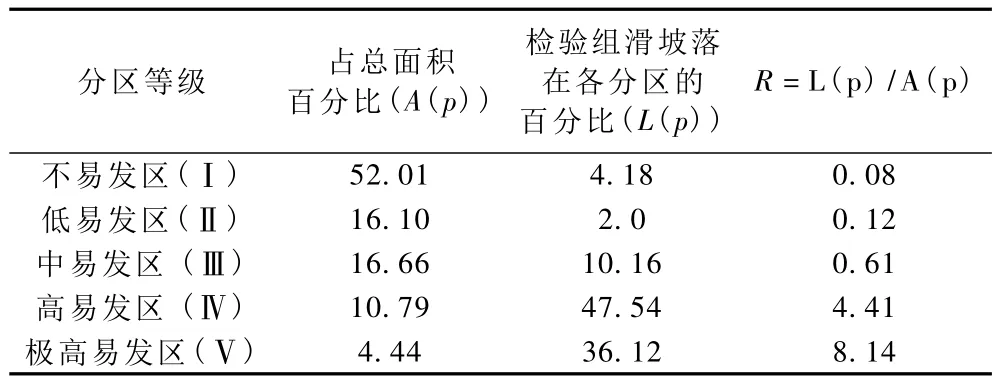
表1 对滑坡易发程度图的检验结果Table 1 Results of verification for the landslide susceptibility map of Zhejiang Province using test samples

4 基于分形丛集方法与一般线性方法的滑坡易发程度区划的对比

从一个县级区的范围将由分形丛集分布方法编制的滑坡易发程度区划图与基于一般线性方法的结果作一个对比。

乐清市(见图5中黑色线框区)在1990～2003年期间由降雨引发并且有坐标记录的滑坡(包括泥石流)为156个，对这些滑坡以25m×25m的网格作为数盒子统计的最小格子。如图6所示，P与r之间的关系可以分为两条直线进行拟合，按式(3)拟合得到分形丛集分布关系为

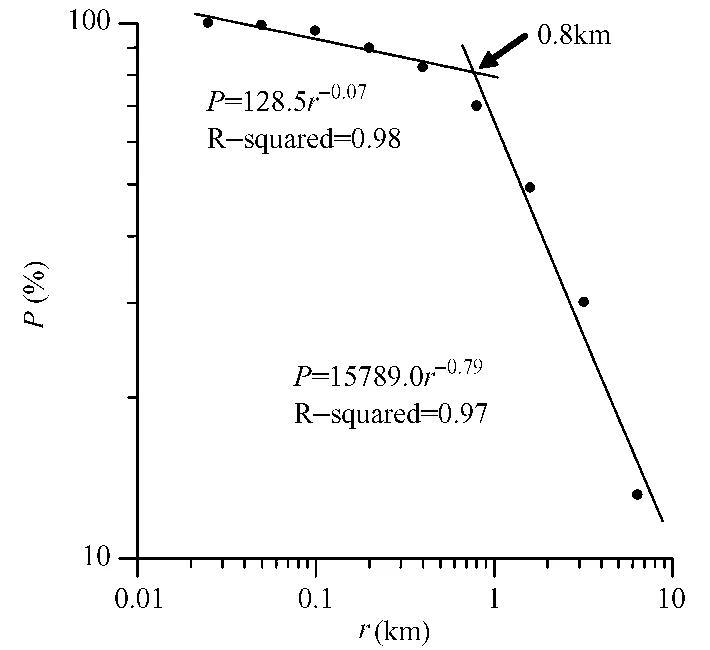
图6 浙江省乐清市在1990～2003年期间由降雨引发的156个滑坡的分形丛集分布(图中横坐标 r表示覆盖研究区的格子尺度，纵坐标P表示在格子尺度为r时含滑坡格子数占格子尺度为rmin时含滑坡格子数的比率)Fig.6 Variation in P with r for 156 landslides triggered by rainfall during the period 1990～2003，Yueqing City，Zhejiang Province.

图6 及式(8)表明在乐清市降雨引发滑坡的分形丛集分布与对全省区域得到的结果不同，它存在两个无标度区:r≤800m和800m＜r≤7000m。对这两个区间分别以100～800m和800～7000m为半径，按照式(8)以每个滑坡点为中心，依次对所有已知滑坡点进行Buffer分析，形成一系列的对应于不同r的Buffer分区，然后得到 P(r)分布图。对 P(r)图按7×7的网格进行光滑处理后，使用4级F函数［参见式(5)］对其进行滑坡易发程度区域划分(即分为不易发、低易发、中易发和高易发4个等级)，按100m×100m网格成图，就得到乐清市1∶1万滑坡易发程度区划图(图7)。

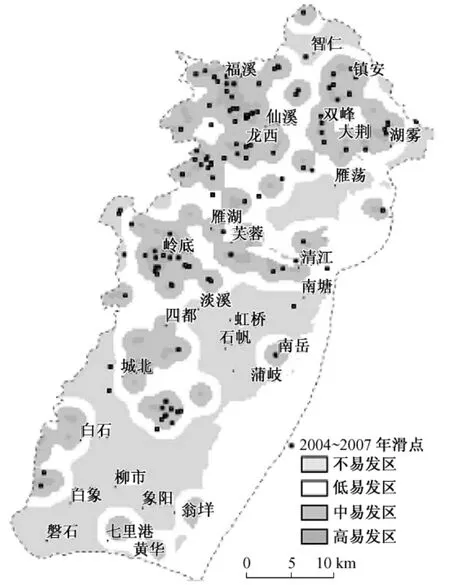
图7 由分形丛集分布方法使用1990～2003年期间发生的156个滑坡数据编制的浙江省乐清市1∶1万滑坡易发程度区划图Fig.7 Landslide susceptibility map of Yueqing City，Zhejiang Province.The map is produced using the fractal clustering relations for the spatial distribution of 156 landslides occurred during the period 1990～2003

图8 是2005年采用传统的一般线性方法，考虑了地质、地形、地貌、植被、年降水量和已知滑坡(包括泥石流)等资料，由主观确定权值①唐小明等，2006，大比例尺地质灾害易发区图编制的方法与实践。编制的浙江省乐清市1∶1万滑坡易发程度区划图，在该图中将滑坡易发程度分为不易发、低易发、中易发和高易发4个等级，图中的白色区表示没有进行滑坡易发程度编图的区域。

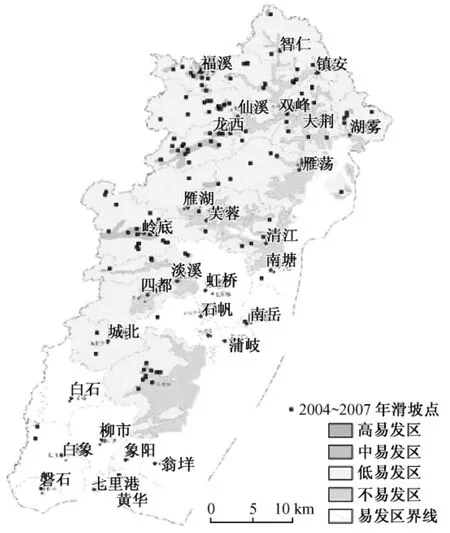
图8 由常规统计方法使用地质、地形地貌、植被、气候和已知的滑坡等6种数据编制的浙江省乐清市1∶1万滑坡易发程度区划图(浙江省地质矿产研究所2005年编制，引自唐小明等①)Fig.8 Landslide susceptibility map of Yueqing City，Zhejiang Province.The map is made by conventional statistical method using 6 data layers including geology，geomorphology，topography，vegetation，climate and landslide inventory

乐清市在2004～2007年期间有记载的因降雨引发的滑坡(包括泥石流)总计为149个，以这些滑坡作为检验样本对图7和图8的预测效果进行检验。将检验组滑坡投在图8上，有8个点落在没有进行滑坡易发程度编图的区域内(见图8中白色区)，其余的141个落在划分出的4个等级区内。为了客观起见，在对图8进行统计时剔出了未进行滑坡易发程度编图的区域(白色区)，只是将已划分出的4个等级区的面积作为总面积计算各分区所占面积百分比，对落在白色区内的8个点也予以剔除，仅按141个滑坡点进行统计。对图7则按照编图区总面积统计各等级区占的面积百分比，并用149个滑坡点进行检验。由表2可见，对于图7，从不易发区→低易发区→中易发区→高易发区，R值依次增大，分别为:0.18、0.30、0.93、8.37;高、中、低三个等级区面积合计占了总面积的66.22%，落在其中的滑坡数占检验样本总数的93.96%，其中，高易发区占总面积的6.82%，命中的滑坡数占57.05%。在图8中，不易发区面积占总面积的18.21%，落在其中的滑坡为13.38%，而低易发区面积占79.25%，落在其中的滑坡也占13.38%，对不易发区检验的滑坡强度(R=0.73)反而要比低易发区(R=0.17)高出4倍之多，这是不合理的;同样，中易发区面积占1.90%，落在其中的滑坡为63.38%，高易发区面积占0.64%，落在其中的滑坡为 9.86%，前者的 R值(33.36)是后者 R值(15.41)的2倍以上，也不甚合理;在图8中，高、中、低三个等级的滑坡易发区占了总面积的81.79%，落在其中的滑坡数占检验样本总数的86.62%，其中，高易发区占总面积的9.86%，命中的滑坡数为15.41%。显然，图7的结果比图8合理，前者的预测能力明显优于后者。

表2 对图8和图9的检验结果对比Table 2 Results of verification for Figures 8 and 9 using test samples

5 讨论和结论

目前用于滑坡易发程度编图的许多方法，无论是统计学方法［6，8，9］，还是基于物理学的方法［11，12］，都需要地形、地质、水文学和土地利用等多种数据。然而，在现有观测条件下获得的各种数据都是不完善的，难免会存在不同程度的不确定性。在这种情况下，使用的数据种类越多，带来的不确定性可能也会随之增加。

本文所提出的评价滑坡易发程度的分形丛集分布方法，虽然只使用了已知的滑坡数据，但是如果这些滑坡都是属于同一种类型，并且是在同一个地质和地理背景下由相同的触发因素(降雨)引发的，在这种情况下，涉及的不确定性也相对较少。另一方面，从表面上看虽然没有使用其它数据，但每一处滑坡之所以发生都是由其所在位置的各种环境因素与触发因素共同作用的结果，滑坡数据本身就隐含有各种相关信息。如果这些滑坡在空间上遵循分形丛集分布，那么在自相似性存在的范围(无标度区)内，这些滑坡的发生就并非是彼此毫不相干的孤立事件，而是存在相互的联系。这也许正如自然界的许多复杂现象一样，其背后隐含的规律往往是简单的。遵循分形丛集分布统计或许正是降雨引发的滑坡在空间分布上的一个基本性质。

本文的研究表明，采用分形统计方法分析已知的滑坡数据，获得滑坡空间分布的分形丛集关系，并在此基础上借助于GIS的空间分析功能可以为评价滑坡易发程度提供一种有效的方法。提出一种对滑坡易发程度区划图的有效性和预测效果进行检验的方法。

在许多易于被降雨引发滑坡，急需获得滑坡易发程度区划图，但又受到资料限制的地区，将分形统计方法与GIS技术结合起来，利用已知的滑坡数据可以获得可靠的滑坡易发程度区划图。

致谢 本项研究得到浙江省重大科技专项 (浙江省地质灾害隐患监测网络系统，计划编号:2006C13024)的支持，特此致谢。

［1］Li C J，Tuhua Ma，Xingsheng Zhu.aiNet-and GIS-based regional prediction system for the spatial and temporal probability of rainfall-triggered landslides［J］.Natural Hazards，2010，52:57-78.

［2］Wadge G.The potential of GIS modelling of gravity flows and slope instabilities［J］. InternationalJournalof Geographical Information Systems，1988，(2):143-152.

［3］Wang Shu-Quiang and Unwin D J.Modelling landslide distribution on loess soils in China:an investigation［J］.International Journal of Geographical Information Systems，1992，6(5):391-405.

［4］Pachauri A K，Pant M.Landslide hazard mapping based on geological attributes［J］.Engineering Geology，1992，32:81-100.

［5］Binaghi E，Luzi L，Madella P.Slope instability zonation:a comparison between certainty factor and fuzzy Dempster-Shafer approaches［J］.Natural Hazards，1998，17:77-97.

［6］Chung C F，Fabbri A G.Probabilistic prediction models forlandslide hazard mapping［J］. Photogrammetric Engineering and Remote Sensing，1999，65:1389-1399.

［7］Guzzetti F，Carrarara A，Cardinali M，Reichenbach P.Landslide hazard evaluation: a review of current techniques and their application in a multi-scale study［J］.Central Italy.Geomorphology，1999，31:181-216.

［8］Lineback G M，Marcus W A，Aspinall R，Custer S G.Assessing landslide potential using GIS，soil wet-ness modeling and topographic attributes，Payette River，Idaho［J］.Geomorphology，2001，37:149-165.

［9］Santacana N，Baeza B，Corominas J，De Paz A，Marturiá J.A GIS-based multivariate statistical analy-sis for shallow landslide susceptibility mapping in La Po-bla de Lillet area(Eastern Pyrenees， Spain) ［J］.Natural Hazards，2003，30:281-295.

［10］Lee S，Ryu J H，Ii-Soo Kim..Landslide susceptibility analysis and its verification using likelihood ratio，logistic regression and artificial neural network models:Case study of Youngin，Korea，Landslide，2007，4:327-338.

［11］Montgomery D R，Dietrich W E.A physically based model for the topographic control on shallow land-sliding［J］.Water Resources Research，1994，30:1153-1171.

［12］Jibson R W，Harp E L，Michael J A.A method for producing digital probabilistic seismic landslide haz-ard maps［J］.Engineering Geology，2000，58:271-289.

［13］Coe J A，Godt J W，Baum R L，Bucknam R C，Michael J A. Landslide susceptibility from topography in Guatemala［J］.Landslides:Evaluation and Stabilization，2004，(1):69-78.

［14］Mandelbrot B B.Self-affine fractals and fractal dimension［J］.Physica Scripta，1985，32:257-260.

［15］陈顒，陈凌.分形几何学［M］.北京:地震出版社，2005.

［16］李长江，麻土华，朱兴盛，等.矿产勘查中的分形、混沌与 ANN［M］.北京:地质出版社，1999.

［17］Organization ofAmerican States，Landslide hazard assessment.In:Primer on Natural Hazard Management in Integrated Regional Development Planning.Washington，D.C.:Natural Hazards Project of the Department of Regional Development and Environment，ExecutiveSecretariat for Economic and Social Affairs，Organization of American States. http://www. oas. org/dsd/publications/Unit/oea66e/begin.htm. Cited 05 Jun 2004.

［18］Anderberg M R.Cluster Analysis for Applications［M］.New York:Academic Press，1973.

Fractal-based landslide susceptibility mapping

LI Chang-jiang1，MA Tu-hua1，SUN Le-ling2，LI Wei2，ZHENG Ai-ping3
(1.Zhejiang Information Center of Land and Resources，Hangzhou 310007，China;2.Zhejiang Provincial Department of Land＆ Mineral Resources，Hangzhou 310007，China;3.Department of Earth Sciences，Zhejiang University，Hangzhou 310027，China)

In this study，we developed a new landslide susceptibility analysis technique using historical landslide inventories and fractal statistics on a GIS platform.We also presented an examining approach to the effectiveness of a landslide susceptibility map.As an illustration of this method application，we measure the spatial fractal clustering distribution of 3285 landslides occurred from 1990 to 2003 in Zhejiang region，a susceptibility map for the region is produced by applying the fractal clustering relation using GIS-supported spatial analysis，and then the 459 landslides，which occurred from 2004 to 2007，are used to examine the effectiveness of the susceptibility map.The verification results show that 384 landslides(accounting for 83.66% of total test samples)fall in the high and very high susceptibility zones which account for 15.23% of total area and 28 landslides(accounting for 6.18% of total test samples)is within the low and very low susceptibility zones which account for 68.11%of total area.

landslide;susceptibility zoning and mapping;fractal method;GIS

1003-8035(2010)02-0017-08

P642.22

A

2009-12-29;

2010-02-26

李长江(1951—)，男，重庆人，教授级高级工程师，主要从事矿产地质和灾害地质研究。

E-mail:zjigmr@mail.Hz.zj.cn