在数学教学中如何渗透德育教育
2010-09-17丁学福
丁学福
随着教学工作的不断深入,笔者逐渐体会到德育教育在数学教学中的重要性、规律性,以及它对学生的健康成长所产生的积极而深远的影响。在实践中,笔者力求结合本学科的特点深入挖掘教材,对学生进行德育教育。
1.结合教学内容,培养学生的辩证唯物主义观念。
(I)“对立统一”观念的培养。圆锥曲线部分提出了解析几何中的两大基本问题:即由曲线求方程,通过方程研究曲线的性质并作出曲线的图形。众所周知,方程和曲线分别是代数和几何学中的两个概念,它们在本质上毫不相干,是对立的。解析几何的研究手段是在采用坐标法的基础上,运用代数法来研究几何图形的性质,使原本毫无联系的两个概念有机地统一起来。因此,笔者在讲解“曲线和方程”这一节时,通过具体实例分析介绍了曲线方程的概念,作了如下小结:平面上的点与有序实数对是一一对应的,即每一点都有坐标与之对应。点的运动形成曲线,曲线上点的坐标受一定条件的制约,即曲线的方程。通过小结,实现了“曲线”与“方程”的对立统一,向学生揭示了解析几何中“数”与“形”的本质联系,培养了学生用“对立统一”的观点观察、分析问题的能力。
又如,在教授“充分、必要条件”一节时,给出了同一命题四种不同表述后,向学生阐明:这四种表述无论是形式,还是侧重点都有区别,是对立的。但所揭示的是同一命题的条件和结论之问的内在联系,反映的实质是相同的,因而又是统一的。通过分析比较,使学生对“对立统一”的认识有了进一步提高。
再如,讲授直线方程后,笔者作了如下小结:直线的点斜式、斜截式、两点式、截距式,这些特殊形式的方程与直线的一般式方程也是既对立,又统一的。说“对立”,是因为它们各自的定义式不同;说“统一”,是因为它们可通过正确的代数变换,特殊形式与一般形式的方程能够相互转化。因此,这些不同形式的直线方程在具有对立性的同时,也具有统一性。
对立统一规律是唯物辩证法的核心,它是学习数学知识的重要指导思想。教师要在教学中结合教学内容,逐渐使学生认识到事物不但有对立的一面,更有统一的一面。培养学生用辩证唯物主义的立场、观点、方法来分析问题和解决问题。
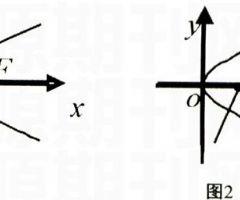
(2)培养学生树立认识问题“由特殊到一般,再由一般到特殊”的方法。教材中经常渗透这种认识问题的规律,教师要善于挖掘教材中质的因素,不失时机地渗透这种观念。如这样一道题:“过抛物线y2=2ρx的焦点的一条直线和这条抛物线相交,两个交点的纵坐标为y1y2,求证:y1y2=-ρ2”该题无论是题意的理解还是思考方法,都具有一定深度。笔者根据学生的特点,将该题作为例题讲授。按照多数学生的理解,往往把题中的直线看成过焦点F与x轴垂直(图1),这样使该题难度大大降低,而且结论也带有偶然性。即特殊性。但从题目条件看,该题的结论对直线又具有一般性。所以上面的理解是片面的、不正确的。为此,笔者将该题做了如下处理:过抛物线y2=2x的焦点的一条直线和这条抛物线相交,两个交点的纵坐标为y1y2,在下列情况下,求y1y2的值:①直线与x轴垂直,②直线的斜率为2,③斜率为k,④斜率为-6。这样变化使求证题改为求解题,结果具有一定的探求性。虽然题目难度增大了,但各问之间形成了阶梯,潜在地发生了某种必然的联系,即蕴含了“由特殊到一般,在由一般到特殊”的认识规律。笔者带领学生完成①、②问,然后启发学生比较①、②两种情况的结果。学生答:“相同。”在此基础上引导学生解答问③,结果仍然是-p2,此时有学生领悟到:原来这条直线不一定与x轴垂直,只要它过焦点与抛物线即可(图2)。笔者因势利导立即给予肯定,阐明了①、②、③问结论间的内在联系,再提出问④时,学生自然地用问③的结论迅速地作出正确结果。
通过该题的教学,培养了学生审题、联想和分析能力,使他们了解“由特殊到一般,再由一般到特殊”的认识规律,给他们树立了运用唯物辩证法学习知识的观念。从而发展了其逻辑思维能力。
2.培养学生理论联系实际、学以致用的观念。数学知识来源于实践。并服务于实践。多数学生只知道学习数学。而对为什么要学习数学,以及它在实际生产生活中的重要作用却知之甚少。这就要求教师在教学中灵活处理教材,不断向学生渗透理论联系实践的观点,激发他们学好数学的热情。数学知识来源于生活和生产,因而它体现的规律可用于实践,从而更好地为生产、生活服务,使学生明确学习不仅为了掌握知识,更重要的是将其用于实践,达到学以致用的最终目的。
3.结合教材进行爱国主义教育。在教学“椭圆的几何性质”一节时,教材例举了用解析法研究椭圆的一个实际应用题——求卫星运行的轨道方程。结合例题,向学生介绍了我国航天技术取得的伟大成就,让他们了解我国是世界上少数几个掌握卫星发射、回收技术的国家之一,并已将这些高科技广泛应用于生产、生活。学生听完后精神振奋,为祖国取得的辉煌成就感到自豪和骄傲,爱国主义情感油然而生。又如,教材中有一道关于圆的方程的习题:“我国古代名桥赵州桥的圆拱跨度37.4米,拱高7.2米,求这座圆拱桥的拱圆的方程。”笔者结合题目,向学生介绍:赵州桥建于隋朝大业年间,保存至今,是一座无墩单孔弧拱券形石桥,全长50.82米,宽89.6米,大拱的净跨度长达37.4米,桥高7.23米。在大券背上各有两个空腔小券。说到这里,笔者问学生:“这座桥在设计上新颖、独特。它具备哪些优点呢?”有的学生说无桥墩便于船只通过;有的说大券上有小券可减轻桥的荷重,节约材料;有的说有小券可泄洪,减少洪水对桥的冲击;还的说弧形圆拱可增加美观……通过讨论,使学生接受了爱国主义教育,并掌握了知识。当然,教材中这样的例子还有很多,教师要根据教学内容适时进行爱国主义教育,做到既教书,又育人。
德育教育是学科教学中不可缺少的重要组成部分,涉及教学的各个方面,因为德育教育不是机械地、呆板地说教。这要求教师在教学中。要认真挖掘教材,探讨在教学中进行思想教育的规律性,从而把德育教育真正放到教育教学的首位,更好地对学生进行思想教育。