正交试验设计法在铅球教学中的运用

方光新 陈雪晴

（1.中国地质大学，湖北武汉 430074；2.铜陵学院，安徽铜陵 244000）

正交试验设计法在铅球教学中的运用

方光新1，2陈雪晴2

（1.中国地质大学，湖北武汉 430074；2.铜陵学院，安徽铜陵 244000）

文章运用正交试验方法来设计最佳铅球教学方案，通过方差分析验证最佳铅球方案各因素的显著性和存在的合理性，为今后在铅球教学训练上提供一个科学定量的标准模式。

正交试验；最佳教学方案；方差分析；标准模式

正交试验设计法是用“正交表”来安排和分析多因素问题试验的一种数理统计方法。这种方法的优点是试验次数少，缩短试验周期，迅速找到优化方案，使用方便。[1]本文试图运用正交设计法对铅球教学手段进行探讨，以确定影响其教学诸因素关系及水平搭配的优化教学方案，给定一个科学的定量标准模式，通过实施以其提高铅球教学成绩。

1.研究对象、方法

为提高所带8个教学班的铅球成绩，探讨铅球教学法以及发展与铅球成绩相关的素质关系，采用下列教学因素与水平进行为期4个月的教学实验。在实验期间，除实验中组织的教学训练外，不得参加其它体育活动。

2.确定所选因素

教学目标的实现不仅取决与因素的优化，而且还取决于因素水平的优化。如果教学目标各因素非常低略，紧靠调整它们之间的水平关系来提高教学目标整体功能，现实中是不可能达到的，也是违背系统论原理的。在铅球技术动作中，最后用力是整个推铅球技术的关键，其动作包括蹬、转、顶、推、拨五个连续动作，其中下肢的蹬和上肢的推最为关键。[2]另外，铅球的投掷姿势也是影响铅球成绩的重要因素。也就是说特定的技术动作和训练效果对应着一定的铅球成绩。因此，根据以上分析，结合实际经验和教学的实际情况，选出下列处方作为试验因素：A上肢力量；B下肢力量；C投掷姿势。因素一旦固定下来，影响成绩的就是实验指标的具体条件即水平。下图是本次实验的因素与水平表，不同因素下不同的水平搭配，给定的实验模式不一样，得出的实验数据也不一样。对于上肢力量来说是选用80%、60%还是选30%更好点；对于下肢力量是选大负荷、小负荷还是跳跃更好。除了这两种因素外，投掷姿势也很重要，是侧向投掷姿势、原地投掷姿势还是背向投掷姿势，这就需要依靠正交试验帮助我们选择一部分有代表性的试验方案，并科学地分析试验结果并从中得出哪种结构模式是最佳优化教学方案。

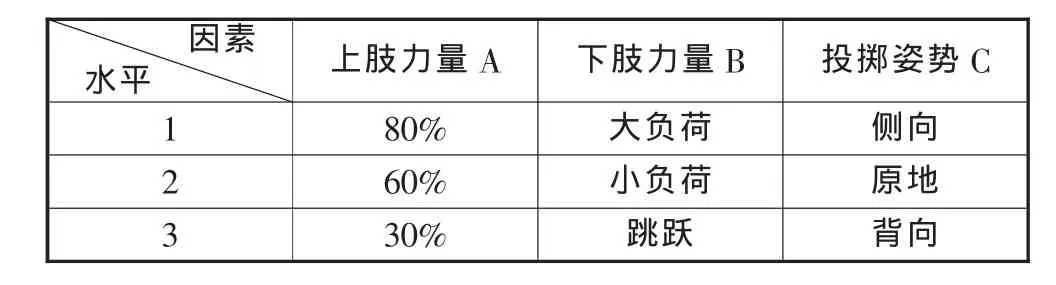
铅球教学实验因素与水平表

3.进行正交试验，确定最优设计方案

将选定的ABC三种因素和三因素下的三个水平，用L9（3）4正交表进行试验(多一栏并不影响结果，还能将此栏作为参照栏进行分析)。最后根据大学体育铅球的评分标准作为试验设计的观察结果，分析并找出主次因素和最佳教学方案。

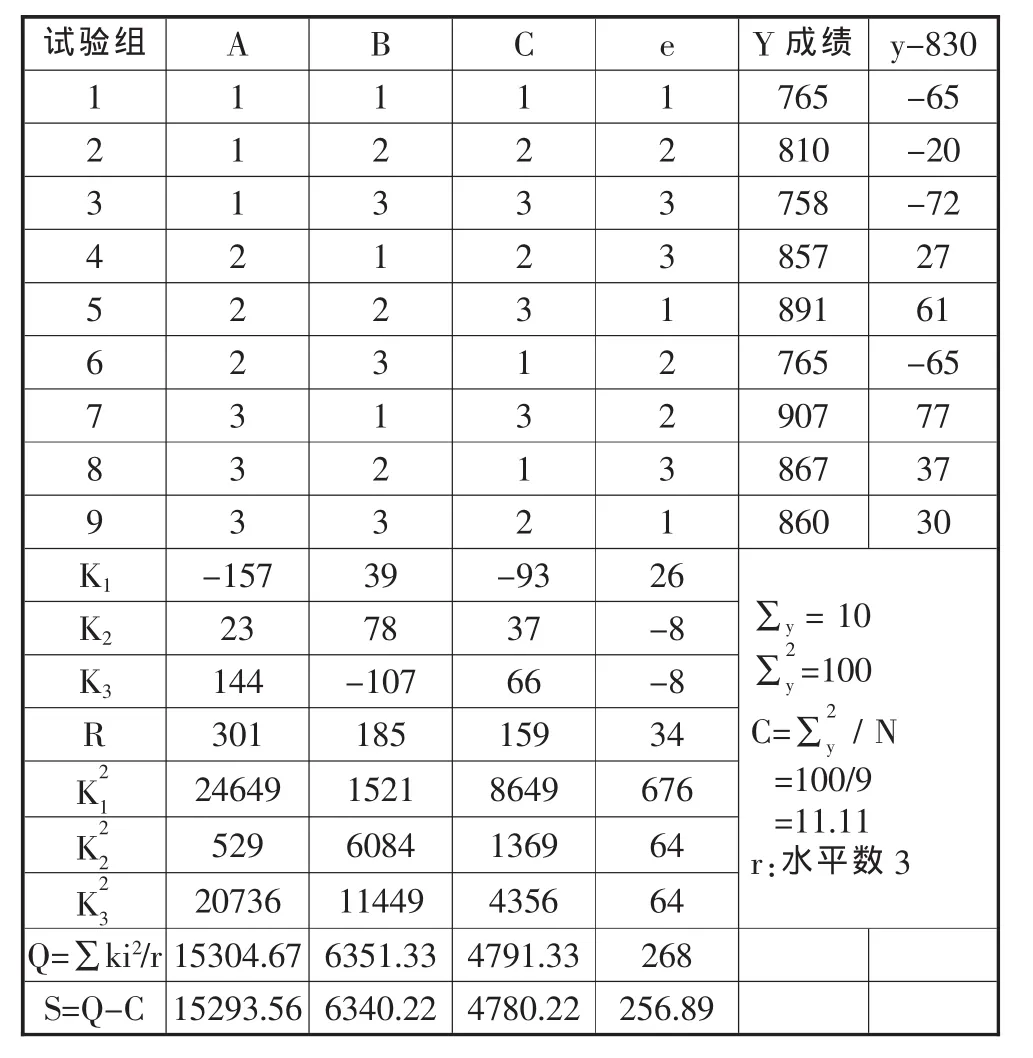
L9（3）4铅球教学试验结果表Y-830（为了简便计算，将所有y成绩减去830）

3.1 确定试验方案步骤，记录并分析试验结果

3.1.1 按照表头设计，A占第一列，B占第二列，C占第三列，水平因子按正交表要求对号入座，这样有9个横行，每一横行就是一个试验方案。

3.1.2 按每个方案要求做试验，把试验结果填入表格右侧。比如：第一组按照1，1，1，1水平进行教学，获得的成绩是765，第二组按照1，2，2，2水平教学，获得的成绩是810，第三组……最后将试验结果成绩依次填入表格右侧。在试验中直接观察的最优方案是第7组试验A3B1C3，训练成绩是907。那么第七组试验是不是各因素结构最优的方案？请看下面的分析。

3.1.3 计算K值，确定最佳设计方案。

分析方法如下，首先把每个因素1水平的所有试验方案结果相加，2水平所有试验方案结果相加，3水平所有试验方案结果相加，选取K值最大的因素进行排列，从而获得最佳试验方案。

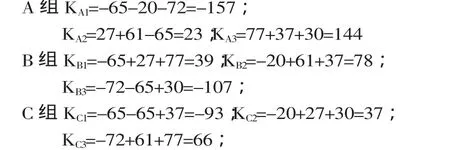
以上结果得出A的K值是KA3最大，B的K值是KB2值大，C的K值是KC2最大，从理论上得出正交试验的最佳方案是A3B2C3，此方案在试验之外，也就是说直接观察的优秀方案A3B1C3并不是最佳方案。优秀教学方案是科学构建教学目标体系、提高铅球成绩的关键之所在，合理的运用、处理好各结构的关系，能为体育课程的改革提供一个可供参考的模式。

3.1.4 计算各因素的极差，分析哪种因素最重要。

各因素K的最大值减去最小值即为极差。

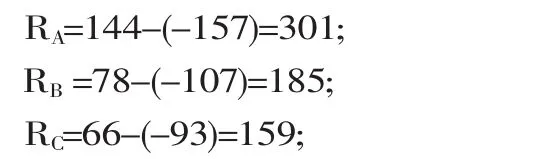
极差的大小说明相应因素对实验结果作用的大小。R值越大的因素重要程度越高，根据极差数据判定主次因素应为A→B→C，也就是上肢力量训练最为关键，它的波动对试验结果影响最大，其次是下肢力量，次之是投掷姿势。为什么可以用极差大小来判定因素的主次?下面我们以数据处理的分组情况入手来进行说明，首先我们来分析A因素KA1、KA2、KA3这三个数值，它对A因素来说分别代表1水平、2水平和3水平的的试验结果，再分析B因素和C因素，发现B因素和C因素的1水平、2水平和3水平均各出现一次，出现机会是均等的，所以可以得出结论，A因素的KA1、KA2、KA3三个K值B因素和C因素对它们无影响，三个K值的不同只是因为A因素水平变化引起的。同理，B因素和C因素的极差，也都是各自水平变化引起的，与其它因素无关。同时正交表还具有整齐可比性决，用极差来分析因素的主次，在数据处理方面也非常方便。

4.分析因素水平（位级）趋势图，搜寻可能更优方案

绘制K值趋势图主要是分析位级与数据结果的联系，搜寻在试验中并没有选取而可能是更好的位级，并以此总结出可能更优秀的教案。为了直观起见，用因素的水平变化为横坐标，指标的K值为纵坐标画出K值趋势图。

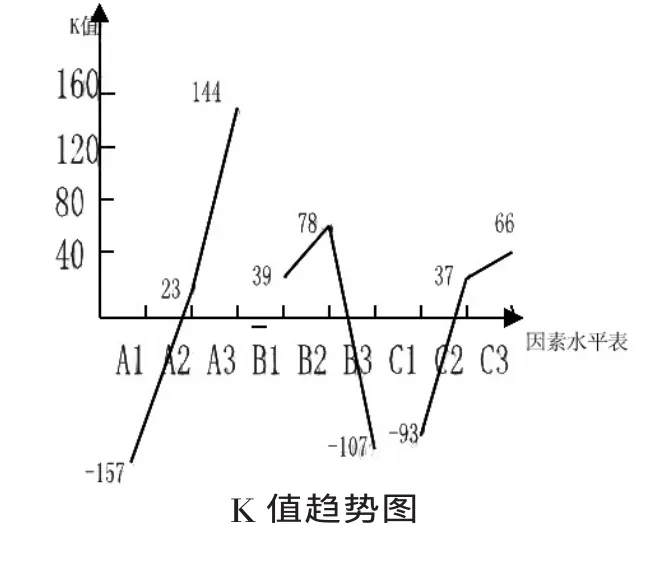
从左图明显看出144、78、66三点最高，按照此因素水平设计的最佳教学方案就是A3B2C3。那么它们是不是铅球教学中的最佳方案？从趋势图得知：上肢力量由80%到60%再到30%时，导致结果之和不断增加，意味着再减小上肢力量的百分比，K值还有上升空间，由此获得的设计方案也许比A3B2C3更优越。

5.通过方差分析表，对最佳方案进行显着性检验。

最佳方案确定的合理性还需方差来验证。

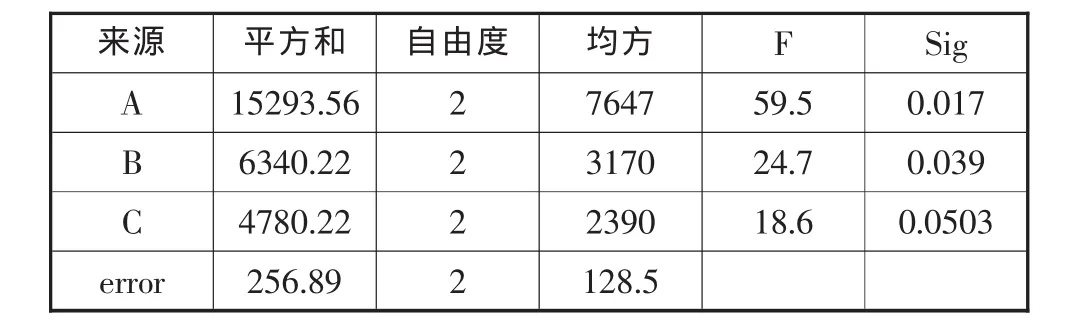
方差分析表

以上各因数在方差分析中验证显著，说明试验是有效的、最佳的。A、B、C搭配的最佳优化方案是A3B2C3，用这种方案进行训练教学，提高学生成绩最显著、最科学。

6.结论与建议

结论：

通过正交试验表分析可以得出三种方案，一种是直接观察的方案A3B1C3，经过了实践证明，在铅球训练教学中要经常关注此项方案进行教学，此方案具有可比性和参考性。另一种是一般计算分析得出的最佳教案A3B2C3，实践证明呈显着性，说明它的存在是合理、科学的。通过极差大小知道主要因素是上肢力量，次要因素是下肢力量，在铅球教学中根据因素主次侧重安排训练教学，提高铅球教学成绩。第三种是通过“趋势图”可能设计出更优方案，尽管未尽试验证明，但在设计更优方案中一定要考虑试验设备、费用等多种因素。对这三种方案的分析使我们对铅球教学方案的认识更加的全面，更加深刻了。

建议：

6.1 由于认识、掌握信息的不同，选取因素和水平指标常常相差很大，若没经过反复的斟酌、对比试验、询问专家（优秀铅球教练），获得的最佳方案结果也不一样，那样极差之间的可比性也就较差。因此，判断因素的重要性最好在掌握较多信息的情况下选择进行。

6.2 影响铅球教学成绩有诸多因素，在抓好技术动作的同时，侧重点加强对成绩有显着影响作用的3个重要因素的教学训练安排。

6.3 在有限的铅球教学时数内，争对学生的实际，运用正交法设计教学训练方案，具有较强的实用性和推广价值。[3]

［1］夏伯忠.正交试验法[M].长春：吉林人民出版社，1985.4-6.

［2］杨建林，贺辉.如何科学设计铅球教学方案[J].北京体育大学学报，2000，23(1):103.

［3］周建伟.正交试验在初中男生1000m跑教学中的运用[J].浙江体育科技，2007，29(1):101.

G642.4

：A

：1672-0547（2010）02-0116-02

2010-03-15

方光新（1970-），女，安徽黄山人，铜陵学院体育部讲师，中国地质大学体育部2008级硕士研究生，研究方向：体育教学与体育教育训练学。