高岭土相转变的非等温动力学

周 佳 何明中张爱华 李 淋 傅凤英

(中国地质大学材料科学与化学工程学院，武汉 430074)

高岭土相转变的非等温动力学

周 佳 何明中＊张爱华 李 淋 傅凤英

(中国地质大学材料科学与化学工程学院，武汉 430074)

高岭土；相转变；差示扫描量热法；非等温动力学；迭代法

高岭土为三斜晶系，一般为无色至白色的细小鳞片，单晶呈假六方板状或书册状，平行连生的集合体往往呈蠕虫状或手风琴状，是造纸、陶瓷、化工、涂料、医药和国防等几十个行业中必须的矿物原料[1]。高岭土相转变的研究是材料学和矿物学研究的热点之一，高温下高岭土相转变产生的莫来石具有较低的热传导系数、热膨胀系数、优良的抗蠕变和热稳定性等性质，可作为高温材料广泛应用于工业生产[2-3]。徐丰平等[4]通过 DSC数据运用Kissinger和Ozawa方程计算得到的高岭土转变为莫来石相变活化能分别为 928.3 kJ·mol-1和 955.4 kJ·mol-1，该过程为一级固相反应，其成核过程为以界面扩散生长为主，但具体的机理函数和指前因子并未给出。而Traore等[5]认为高岭土在950～1020℃时成核与晶体生长同时进行，XRD和微晶实验证实该过程为非均相同时转变为尖晶石和莫来石，不能以Arrhenius公式计算得到重结晶的动力学参数。本工作以广东茂名高岭土为原料，研究了高温下高岭土由偏高岭土转变为莫来石过程。通过迭代的等转化率法求算高岭土相转变的活化能，以最小偏差法得到最可能机理函数，最后求得指前因子，从而得到完整的动力学三因子。

1 实验部分

1.1 试剂与仪器

高岭土产自广东茂名，其主要成分为：46.28%SiO2；38.15%Al2O3，平均粒度为：2 μm。德国 Netzsch公司STA 409 PC综合热分析仪。荷兰PANalytical公司X′Pert PRO Dy 2198 X射线衍射仪。

1.2 实验条件

综合热分析仪： 高岭土用量为 18.40～18.81 mg；升温速率分别为 5、10、15、20、25 及 30 ℃·min-1；扫描温度范围为 30～1200℃；空气流量为 30 mL·min-1。

X射线衍射仪：Cu Kα靶；管电流80 mA；管电压 40 kV；步长 0.02°；扫描角度 10.00°～65.00°。

2 基本原理

2.1 迭代法计算活化能

在升温速率恒定时，非等温动力学方程有如下形式：

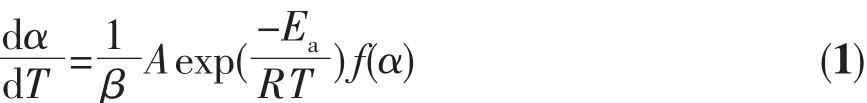
式(1)中，α为转化率；f(α)为动力学机理函数；β为升温速率；Ea为活化能；A为指前因子；T为该转化率下的反应温度；R为普适气体常数。设u=Ea/(RT)，对式(1)进行移项并两端同时进行积分得：

温度积分公式P(u)在数学上得不到精确解，常常由近似公式代替。采用Dolyle近似式[6]得Ozawa方程：

采用Coats-Redfern近似式[7]得到KAS方程：

由于式(3)和式(4)引入了温度积分近似公式，在计算Ea时会产生一定的误差。本文采用迭代法[8]即Ozawa迭代法和KAS迭代法来求算Ea。若P(u)取Senum-Yang 近似[9]可得：

Ozawa迭代方程:

H(u)和h(u)随着u的变化而变化，它们分别为方程(5)和(6)进行迭代的定义函数，其定义式为：

迭代过程可分为三步：步骤一，假设H(u)=1或h(u)=1，代入方程(5)或(6)中，并以 ln[β/H(u)]对 1/T 或ln{β/[h(u)T2]}对1/T进行线性回归，通过斜率可求得初始的活化能Ea1，即为常规的等转化率法所求得的Ea值；步骤二，将Ea1值以及不同升温速率条件下同一转化率时所对应的T代入u以及H(u)或h(u)的定义式中，求取u及相应的H(u)或h(u)的值，再将H(u)或h(u)的值代入方程(5)或(6)中线性回归，可求得新的Ea2值；步骤三，以Ea2代替Ea1，重复步骤二，直至 Eai-Ea(i-1)＜0.01 kJ·mol-1时，即可认为所求得的活化能值为真实值[10]。在不同的α处采取相同的步骤得到α与Ea的关系，如果在主要的α范围内(0.2≤α≤0.8)，活化能的数值基本不变，则可以认为该反应可以用单一的动力学模型来描述[11]。

2.2 判定最可能的机理函数

主曲线法[12]是一种判定最可能的机理函数的方法，它是以实验曲线和标准曲线的最大重叠或曲线相近作为判定的依据，最小偏差法则是以实验值和理论值大小差别作为判定依据，从定量方面来看更具优势。最小偏差法求算最可能的机理函数过程如下：

以α=0.5作为参考点，由式(2)可以得到：

为了更加精确地计算P(u)，可采用一个准确度高的温度积分近似表达式[13-14]。

将迭代法计算得到的活化能的平均值和各α(0.16≤α≤0.84，间隔 0.02)处对应的温度 T 值代入式(9)左端计算出 P(u)/P(u0.5)的值，构成实验值；将 45种机理[15]对应的 G(α)代入式(9)的右端计算出 G(α)/G(α0.5)的值，构成理论值。计算实验值和理论值之间的标准偏差，根据标准偏差的大小可以找到合适的机理函数。标准偏差的计算公式如下[16]：

式(11)中，k为机理的序号，m和n分别为数据点和升温速率的数目。当Gk(α)为最可能的机理函数时，Δ数值最小。

2.3 指前因子求解

确定机理函数G(α)之后，将其代入到式(2)中，移项并两边取对数得：

当升温速率为一定值时，把温度积分近似表达式，活化能平均值和各转化率对应的温度代入式(12)的左端，设定的转化率代入上式的右端，用ln[Ea/(βR)]+lnP(u)对 lnG(α)作图，可得到一条直线，根据直线的截距可得到lnA的值，计算得到不同升温速率下的lnA，就得到指前因子的变化范围[17]。

3 结果与讨论

3.1XRD分析

图1是高岭土原样(曲线a)以及经过850℃(曲线b)和1 200℃(曲线c)煅烧后样品的XRD图，曲线a衍射峰的峰型尖锐且对称性好，与标准卡片No.74-1784对比可知样品为高岭土；曲线b几乎没有明锐的衍射峰，呈现典型的无定形结构，没有明显的晶型存在，即高岭土经过850℃煅烧后转变成非晶态偏高岭土；曲线c与标准卡片No.06-0258对照，证实该晶态物质为莫来石，表明样品经过1200℃煅烧后重新结晶并生成新的晶态物质[1,18]。

3.2TG-DSC分析

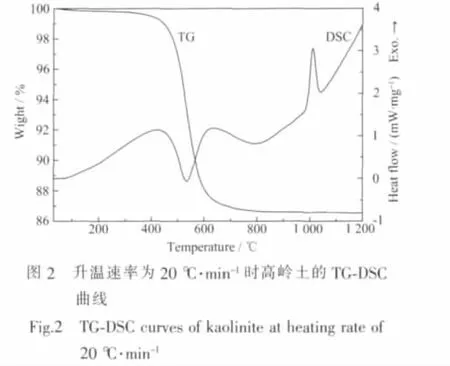
图2是升温速率为20℃·min-1时高岭土在30～1200℃之间的TG-DSC曲线，由图可知高岭土在400～700℃之间发生热分解反应，其对应为高岭土分子内羟基的脱除[19]，实际平均失重率(13.56%)与理论失重率(13.96%)相吻合。在 975～1040℃之间，DSC曲线上有一个尖锐的放热峰，而在相同温度区间，热重曲线计算表明失重率小于0.1%，故在此温度区间样品应发生了相转变过程。

综合XRD和TG-DSC的结果表明，在975～1040℃之间，样品发生了相转变过程，由非晶态的偏高岭土转变成为莫来石，这与文献[20]报道的相符。

3.3 相转变动力学

图3为不同升温速率下900～1 100℃高岭土的DSC曲线。根据DSC曲线所对应的数据，运用2.1中求活化能的4种方法对高岭土相转变过程的活化能进行计算，得到不同转化率时相对应的活化能的值，见表1。

由表1可以看出，由Ozawa法和KAS法所得活化能结果相差 21.04 kJ·mol-1，而由 Ozawa 迭代法和KAS迭代法计算的结果基本一致，所得活化能相差仅 0.52 kJ·mol-1。鉴于两种迭代法分别为 Ozawa法和KAS法的改进，故取二者所得活化能的平均值作为高岭土相转变所需活化能，即 Ea=840.44 kJ·mol-1。

采用2.2中所述方法，将实验数据代入式(9)左端，计算得到 P(x)/P(x0.5)的值，将 45种机理对应的G(α)代入式(9)右端计算出 G(α)/G(0.5)的值。根据最小偏差法对实验值和理论值进行处理，表2中列出了其中较优的6种机理及其对应的标准偏差，由表可知第11号机理所对应的标准偏差最小，应为高岭土相转变过程的最可能机理，该机理为随机成核和随后生长机理，对应的机理函数为G(α)=[-ln(1-α)]1/3，相应的微分式为 f(α)=3(1-α)[-ln(1-α)]2/3。

表2 高岭土相转变对应的较优机理Table 2 Better mechanism of phase transformation of kaolinite

由2.3的计算方法得到不同升温速率下的指前因子A，如表3所示。从表3可知：斜率均接近1，相关系数r≥0.9922，线性关系较好，这也进一步表明了本文求得的高岭土相转变机理的准确性。计算得该指前因子 A 范围为 1.54×1034～1.65×1034s-1。

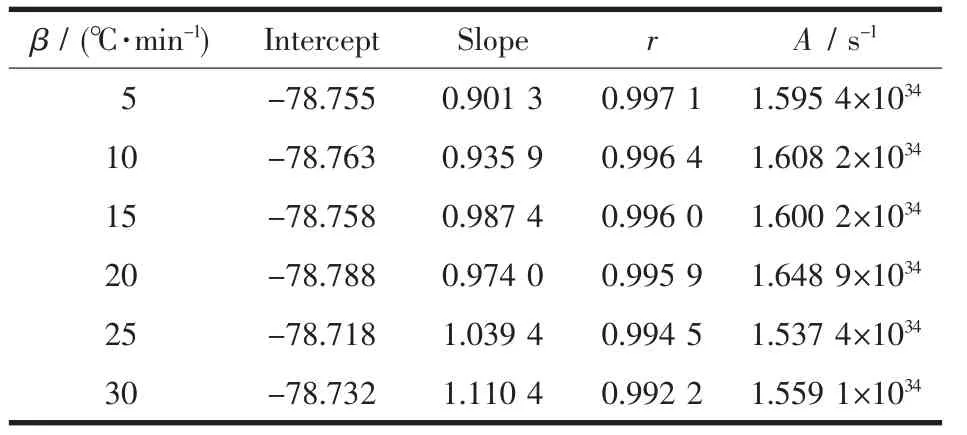
表3 高岭土相转变在不同加热速率时对应的指前因子Table 3 Pre-exponential term of the phase transformation of kaolinite at different heating rates

4 结 论

在动态空气气氛条件下，本文所用高岭土在975～1 040℃的温度范围内相转变生成莫来石的过程符合Arrhenius公式，其相转变的活化能Ea=840.44 kJ·mol-1；以最小偏差法得到最可能机理函数，机理为随机成核和随后生长，机理函数的微分和积分表达式分别为 f(α)=3(1-α)[-ln(1-α)]2/3和G(α)=[-ln(1-α)]1/3；指前因子 A 的范围为 1.54×1034～1.65×1034s-1。

致谢： “纳米矿物材料及应用教育部工程研究中心”的严春杰教授为本实验提供高岭土样品，在此表示衷心感谢。

[1]WANG Xue-Jing(王雪静),ZHANG Jia-Min(张家敏),LI Xiao-Bo(李 晓 波),et al.China Non-Metall.Mining Indu.(Zhongguo Feijushu Kuangye Daokan),2007,5:18-20

[2]WEI Cun-Di(魏存弟),MA Hong-Wen(马鸿文),YANG Dian-Fan(杨 殿 范),et al.J.Chin.Ceram.Soc.(Guisuanyan Xuebao),2005,33(1):77-81

[3]Aksay A,Dabbs D M,Sarikaya M.J.Am.Ceram Soc.,1991,74(10):2341-2346

[4]XU Feng-Ping(徐丰平),CHEN Nan-Chun(陈南春),AO Hai-Mei(敖 寒 梅).Ind.Miner.Proce.(Huagong Kuangwu Yu Jiagong),2008,4:12-14

[5]Traore K,Gridi-Bennadji F,Blanchart P.Thermochim.Acta,2006,451:99-104

[6]Doyle C D.J.Appl.Polymer Sci.,1961,5(15):285-292

[7]Coats A W,Redfern J P.Natrue,1964,201(4914):68-69

[8]Gao Z,Nakada M,Amasaki I.Thermochim.Acta,2001,369:137-142

[9]HU Rong-Zu(胡荣祖),GAO Sheng-Li(高胜利),ZHAO Feng-Qi(赵凤起),et al.Thermal Analysis Kinetics.2nd Ed.(热分析动力学.2版).Beijing:Science Press,2008.241-242

[10]ZHANG Wei-Nan(张伟男),YUAN Yu-Hong(袁誉洪),LI Li-Qing(李丽清),et al.Acta Phys.-Chim.Sin.(Wuli Huaxue Xuebao),2004,20(1):33-37

[11]GUAN Chun-Xiou(关春秀),CHEN Dong-Hua(陈栋华).J.South-Central Univ.Nationalities:Nat.Sci.Ed.(Zhongnan Minzu Daxue Xuebao:Ziran Kexue Ban),2004,23(1):14-17

[12]TANG Wan-Jun(唐万军),YANG Xi(杨 洗),LIU Yu-Wen(刘欲文),et al.J.Wuhan Univ.:Nat.Sci.Ed.(Wuhan Daxue Xuebao:Ziran Kexue Ban),2004,50(6):675-676

[13]Urbanovici E,Popescu C,Segal E.J.Therm.Anal.Cal,1999,55(1):325-327

[14]Senum G I,Yang R T.J.Them.Anal.,1977,11(3):445-447

[15]HU Rong-Zu(胡荣祖),GAO Sheng-Li(高胜利),ZHAO Feng-Qi(赵凤起),et al.Thermal Analysis Kinetics.2nd Ed.(热分析动力学.2版).Beijing:Science Press,2008.151-155

[16]TANG Wan-Jun(唐万军),CHEN Dong-Hua(陈栋华),WU Ming(伍 明).J.South-Central Univ.Nationalities:Nat.Sci.Ed.(Zhongnan Minzu Daxue Xuebao:Ziran Kexue Ban),2007,26(1):16-19

[17]QIN Fang-Fang(秦芳芳),HE Ming-Zhong(何明中),CUI Jing-Wei(崔景伟),et al.Chem.J.Chinese Universities(Gaodeng Xuexiao Huaxue Xuebao),2007,28(12):2343-2348

[18]WEI Cun-Di(魏存弟),MA Hong-Wen(马鸿文),YANG Dian-Fan(杨殿范),et al.Bull.Chin.Ceram.Soc.(Guisuanyan Tongbao),2005,2:13-16

[19]ZHANG Ai-Hua(张爱华),HE Ming-Zhong(何明中),QIN Fang-Fang(秦芳芳),et al.J.Chin.Ceram.Soc.(Guisuanyan Xuebao),2009,37(10):82-86

[20]LIU Zhen-Hai(刘振海),Hatakeyama(畠山立子).Manual of Analysis Chemistry(分析化学手册).Beijing:Chemical Industry Press,2000.242-243

Non-Isothermal Kinetics for Phase Transformation of Kaolinite

ZHOU Jia HE Ming-Zhong＊ZHANG Ai-Hua LI Lin FU Feng-Ying
(Faculty of Material Science and Chemical Engineering,China University of Geosciences,Wuhan 430074)

The process of phase transformation of kaolinite was investigated by differential scanning calorimetry(DSC)and X-ray power diffraction(XRD).The iterative procedure along with the minimum deviation was employed to determine the kinetic parameters of phase transformation of kaolinite.Results show that the kaolinite phase transformation occurs from the metakaolin into mullite in the temperature range 975～1 040 ℃.The kaolinite phase transformation conforms to an accommodated nuclei production and nuclei growth model.The corresponding mechanism functions are f(α)=3(1-α)[-ln(1-α)]2/3and G(α)=[-ln(1-α)]1/3.The activation energy Eaand preexponential factor A of kaolinite phase transformation are 840.44 kJ·mol-1and 1.54×1034～1.65×1034s-1,respectively.

kaolinite;phase transformation;DSC;non-isothermal kinetics;iterative method

O643.12

A

1001-4861(2010)07-1279-05

2010-03-10。收修改稿日期：2010-03-29。

国家自然科学基金资助项目(No.50972135)。

＊通讯联系人。E-mail：hmzhong@126.com

周 佳，男，24岁，硕士研究生；研究方向：热分析动力学。