测量不确定度评定的见解
2010-09-15张志清山西省医疗器械检测中心太原030012
张志清 山西省医疗器械检测中心 (太原 030012)
测量不确定度评定的见解
张志清
山西省医疗器械检测中心 (太原 030012)
不确定度是国际公认的用来评定测量结果质量的参数,是报告度量的尺度。准确、合理的不确定度评定,是提供正确测量结果的前提和保证,因此,本文对不确定度的评定内容进行了论述,并以低频治疗仪脉冲输出能量的不确定度评定为例,分析了不确定度评定的过程和方法。
不确定度 测量误差 自由度 包含因子
1 测量不确定度的概念
不确定度是表征合理赋予被测量之值的分散性,与测量结果相联系的参数,测量不确定度是考虑对测量影响的各种因素在受控于统计状态之下,对一个量在相同条件下进行了多次测量,其测量结果不是同一值,是以一定概率分布在某一区域内的许多值,这个分散性用不确定度定量描述,测量不确定度与测量结果在一起,构成最终测量的完整表达式。
测量不确定度的来源测量结果是测量的要素之一,而其他测量要素,如测量对象、测量资源、测量环境等均会在测量过程中对测量结果产生不同程度的影响。对测量结果会产生影响的因素,可能来自于以下几个方面:
实现测量的定义不完整或不完善;取样的代表性不够;对测量过程受环境影响的认识不周全或对环境条件的测量与控制不完善;模拟式仪器的读数存在人为偏移;仪器计量性能的局限性,测量仪器的分辨力或鉴别力不够;赋予测量标准和标准物质的标准值不准确;引用常数或其他参量不准确;与测量方法和测量程序有关的近似性或假定性;在表面上看来完全相同的测量条件下被测量重复观测值的变化等。
2 测量不确定度与测量误差的区别
测量误差是某待测物的测得值与“真值”之间的差,只决定于测量结果。测量不确定度是定量表示对测量结果的怀疑程度,测量结果的不确定度决定于所采用的测量原理、方法、测量仪器、参考标准、引用的值、测量条件和人员水平。比较测量不确定度与测量误差,两者的定义既有联系,又有截然的不同之处。所谓联系是指两者都与测量结果有关,而且两者是从不同角度反映了测量结果的质量指标。对于测量误差在严格意义上是主观不可知的,但在已知约定真值的情况下测量误差又是可知的,测量误差主要是用在测量过程中对误差源的分析,即通过这样的误差分析,设法采取措施达到减小、修正和消除误差的目的,提高测量的质量水平。对于不确定度,人们在主观上是完全可以根据所掌握的有关测量结果的数据信息来估计,不确定度的大小决定了测量结果的使用价值,成为一个可以操作的合理表征测量质量的一个重要指标,不确定度小,说明该测量结果的质量好,使用价值大,其测量的质量水平高,反之则效果相反,当然,不确定度也可用于最终对测量结果中所含误差的分析与处理。
3 不确定度的分类与评定
3.1 不确定度的A类评定
(1) 不确定度的A类评定定义:用对观测列进行数理统计方法进行评定。
(2) 评定方法
被测量x在重复条件下进行n次重复测量,观测值为xi(i = 1,2,…,n),算术平均值x-为:

单次测量的实验标准偏差由贝塞尔公式计算:
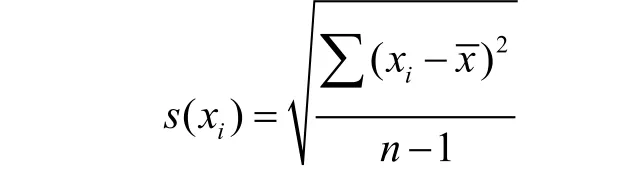
平均值的实验标准偏差为:
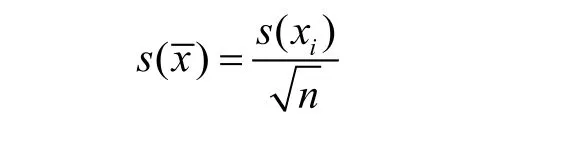
当测量结果取任一观测值时,所对应的A类不确定度标准不确定度为:u(xi) = s(xi),A类相对标准不确定度:
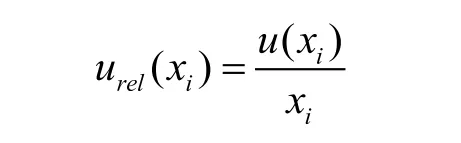
当测量结果取n次的算术平均值时,所对应A类不确定度的标准不确定度为:
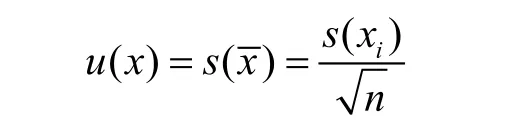
A类相对标准不确定度:

当取若干组观测值,它们各自的平均值也散布在期望值附近,但比单个观测值更靠近期望值。也就是说,多次测量的平均值比一次测量值更准确,随着测量次数的增多,平均值收敛于期望值。因此,通常以样本的算术平均值作为被测量值的估计(即测量结果),以平均值的实验标准差s(x-)作为测量结果的标准不确定度,即A类标准不确定度。(3) A类不确定度的自由度
在方差计算中,自由度为和的项数减去对和的限制数,即为v。被测量x在 n次独立测量样本方差为:
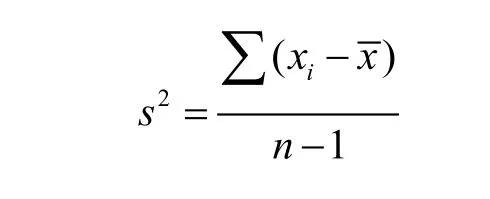
A类不确定度的标准差,即A类不确定度的不确定度以σ(u)表示,则A类相对不确定度的不确定度和自由度v的关系为:
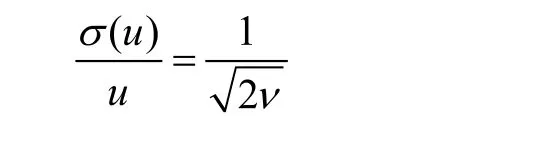
由此可以看出,自由度越大,相对不确定度越小,不确定度的可靠程度越高。一般情况下应n>5。
(4) 测量A类不确定度需要注意的几点:
不确定度是指测量结果的不确定度,不是指仪器的不确定度。如要反映仪器的不确定度,应在全量程内选取波动最大的点测量计算不确定度。当反映仪器不确定度时,如不确定度以绝对形式表示,应选全量程的最大点进行测量和计算(如千分尺)。如不确定度以相对形式表示,应选全量程的最小点进行多次测量(如材料试验机),用以代表全量程各点。当反映仪器不确定度时,可以在全量程内选取多点测量,以代表全量程,如选取m点,每点测n次,单次测量不确定度为:
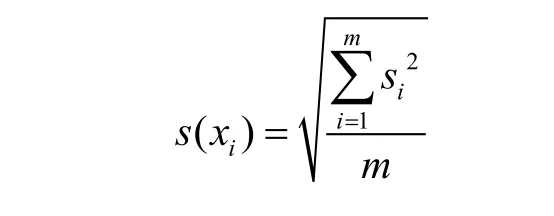
si为各点n次测量实验标准差。
平均值不确定度:

其中自由度为v = m(n–1)
3.2 不确定度的B类评定
(1) 不确定度的B类评定定义:用被测量可能变化的有关信息和资料进行评定。
B类标准不确定度以u(x)表示,则相对B类标准不确定度以表示。
(2) 信息来源
以前的观测数据。对有关技术资料和测量仪器特性的了解和经验。生产部门提供的技术说明文件。检定证书,校准报告或其它文件提供的数据、准确度等别或级别。手册或某些资料给出的参数数据及其不确定度。规定实验方法的国家标准或类似的技术文件中给出的重复性限r和复现性R。
(3) 评定方法
① 已知置信区间和包含因子
根据经验和有关信息或资料,分析判断落入区间[x-–a, x-+a]的概率分布,估计包含因子k,则几种常见分布关系见表1。

表1 常见分布关系
在缺少任何信息的情况下,一般估计为矩形分布。如被测量xi出现在中心附近的概率大于区间边界时,最好估计为三角分布。如果xi本身是几个观测值的平均值,则估计为正态分布。
② 已知扩展不确定度U和包含因子k,来源于仪器说明书、校准报告、手册或其它资料,则
③ 已知扩展不确定度Up和置信水平(置信概率)p的正态分布,来源于检定证书或校准报告,
④ 已知扩展不确定度Up以及置信水平p与有效自由度veff的t分布,来源于检定证书或校准报告,根据t分布表,由p和veff查得tp(v)值(t值),则
⑤ 由重复性限、复现性限求不确定度。
由于重复性是在相同测量条件下,对同一被测量进行连续多次测量所得结果的一致性,建议若有重复性限 r,重复实验结果又满足它的要求,则可用 r/2.83作为A类不确定度;复现性是在改变了的测量条件下,同一被测量的测量结果之间的一致性,建议若有复现性限 R,又没有其它重要影响量,则可用 R/2.83作为合成标准不确定度。
⑥ 以“等”使用的仪器不确定度的计算
一般采用正态分布或t分布计算,如标准砝码,所需数据由检定证书或校准报告给出。
(4) B类不确定度的自由度
B类不确定度的标准差,即B类不确定度的不确定度以σ[u(xi)]表示。
由于很难计算σ[u(xi)]得出自由度,只能定性判断估计。一般情况下,当有严格数字关系,如数显仪器的分辨力、最大允许误差和数据修约引起的不确定度的计算,自由度为∞。当数据来源检定证书,校准报告或手册等可靠资料时,可取较高自由度;当计算带有一定主管判断因素,如模拟仪器的读数误差引起的不确定度,可取较低自由度。当信息来源于难以用有效实验方法验证时,如量块检定时,标准量块与被检量块温度差的不确定度,自由度可以非常低。
3.3 合成标准不确定度的评定
(1) 合成标准不确定度的概念
以上A类、B类不确定度都是对某一被测量通过测量统计计算或根据资料信息经计算得出的,其实在很多情况下,被测量不能直接测量得出,而是按若干个输入量的方差和协方差算得的标准不确定度,称为合成标准不确定度。当合成标准不确定度以uc(y)表示时,则相对标准不确定度以
(2) 评定方法
对于y = f(x1, x2……, x1, ),当xi彼此独立或不相关时,


在评定工作中,对于同一仪器,同一变量,相同量纲(一般无固定关系式)一般采用绝对形式(也可采用相对形式),即符合的形式。
比如滴定管体积不确定度:
u1(V):由最大允许误差引入的不确定度。
u2(V):由温度波动引入的不确定度。
如若求不确定度的绝对形式uc2(y)很复杂,但其相对形式相当简单。
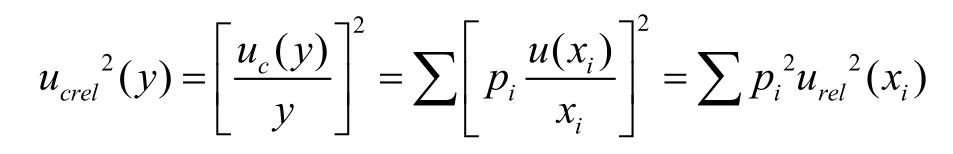
在评定工作中,对于不同仪器,不同变量,不同量纲(一般有固定关系式)应采用相对形式,即符合的形式,即变量相乘积的形式。
如将上式滴定管体积不确定度与取样量不确定度合成相对合成不确定度:

(3) 合成不确定度的自由度
合成不确定度的自由度称为有效自由度。有效自由度可由韦尔奇-萨特思韦特公式计算:
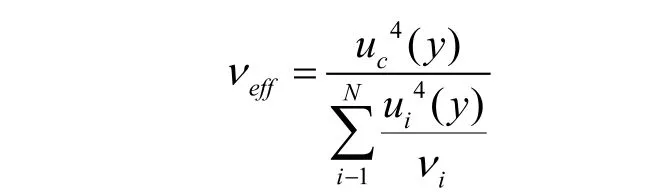
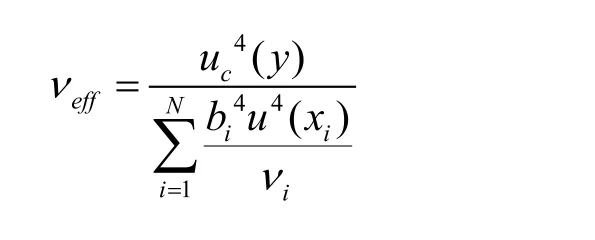
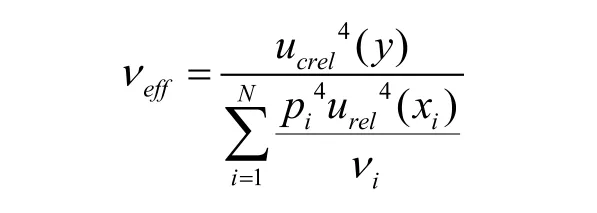
3.4 扩展不确定度
(1) 扩展不确定度的概念
用扩展不确定度来表示测量结果的分散性大小,是在合成不确定度 前面乘上一个系数(包含因子)所构成。它有两种形式:

当Uc的自由度较大时,适应,k取2 (置信概率p=95%)或3(置信概率p=99%)。当Uc的自由度较小时,适应,根据置信概率p和合成不确定度的自由度veff查t分布表,查得值,置信概率p可取95%和99%,当与输出估计值相关的标准差的可靠性足够高时,一般可取95%。
(2) 包含因子的选择
4 应用实例
用一台数字万用表测量和一台示波器测量低频治疗仪在额定负载电阻下单个脉冲的输出电压和脉冲宽度,然后计算出单个脉冲输出能量的不确定度并写出报告。
(1) 测量电阻的不确定度
① 读数重复性引入的A类不确定度
用一台数字万用表测量标称值500Ω的额定负载电阻,连续测量10次,得到如下数据,如表2所示:

表2 额定负载电阻测量记录
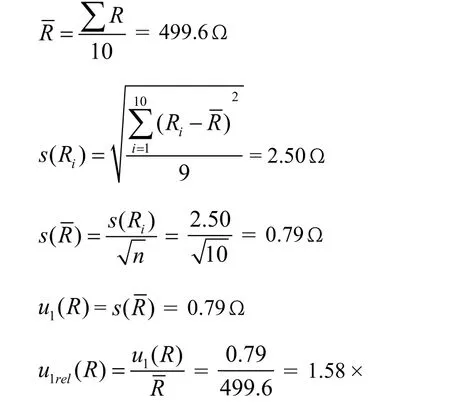
② 测量误差引入的B类不确定度
测量额定负载电阻用的是3位半(满刻度1999字)数字万用表,2kΩ电阻量程(对应1Ω/1个字),测量误差a = 0.5%读值+ 1个字= 0.5%×499.6Ω + 1Ω=3.50Ω,属矩形(均匀)分布,k =

③ 分辨力引起的B类不确定度
数字万用表测量电阻的分辨力为1Ω,数字示值分散区间半宽,即0.5Ω,并取均匀分布,其标准不确定度为:
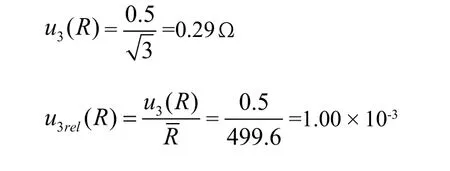

(2) 测量脉冲电压的不确定度
① 读数重复性引入的A类不确定度
用一台数字示波器测量低频治疗仪在额定负载电阻下单个脉冲的脉冲电压,连续测量10次,得到如下数据,如表3所示:

表3 脉冲电压测量记录
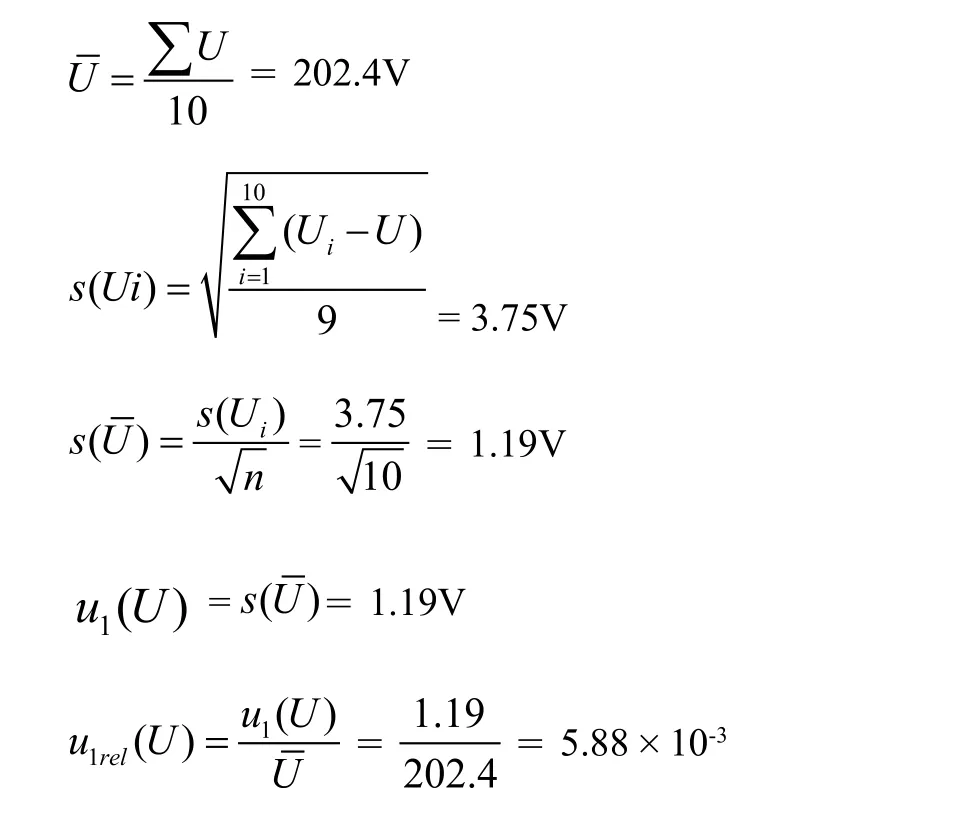
② 测量误差引入的B类不确定度
用数字示波器测量脉冲电压时,测量误差a = 1%读数= 1%×202.4V = 2.02V,属矩形(均匀)分布,k
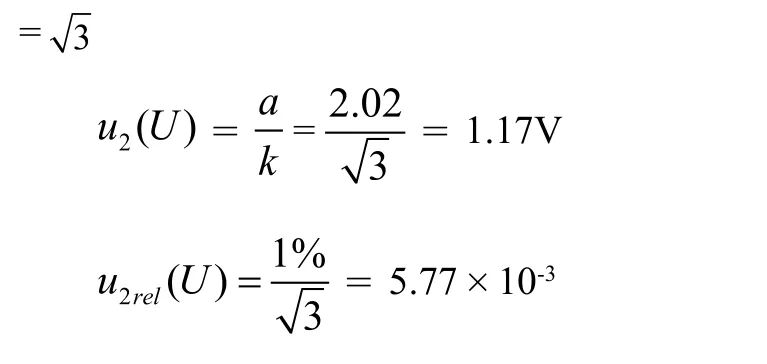
③ 分辨力引起的B类不确定度
数字示波器测量脉冲电压的分辨力为2V,数字示值分散区间半宽,即1 V,并取均匀分布,其标准不确定度为:
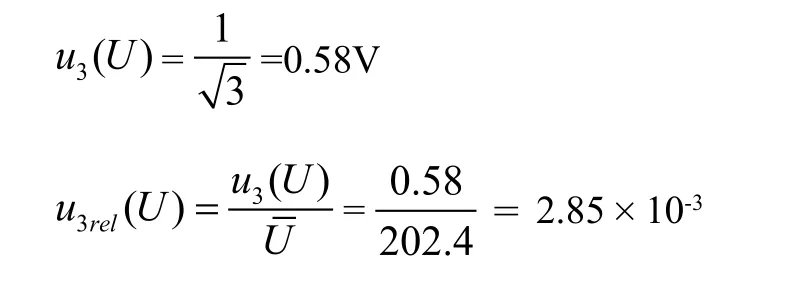
脉冲电压不确定度由以上三项合成
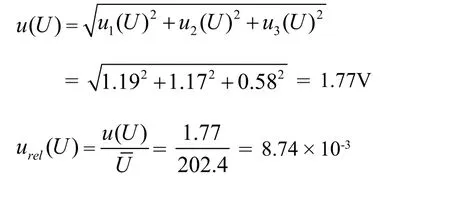
(3) 测量脉冲宽度的不确定度
① 读数重复性引入的A类不确定度
用一台数字示波器测量低频治疗仪在额定负载电阻下单个脉冲的脉冲宽度,连续测量10次,得到如下数据,如表4所示:

表4 脉冲宽度测量记录
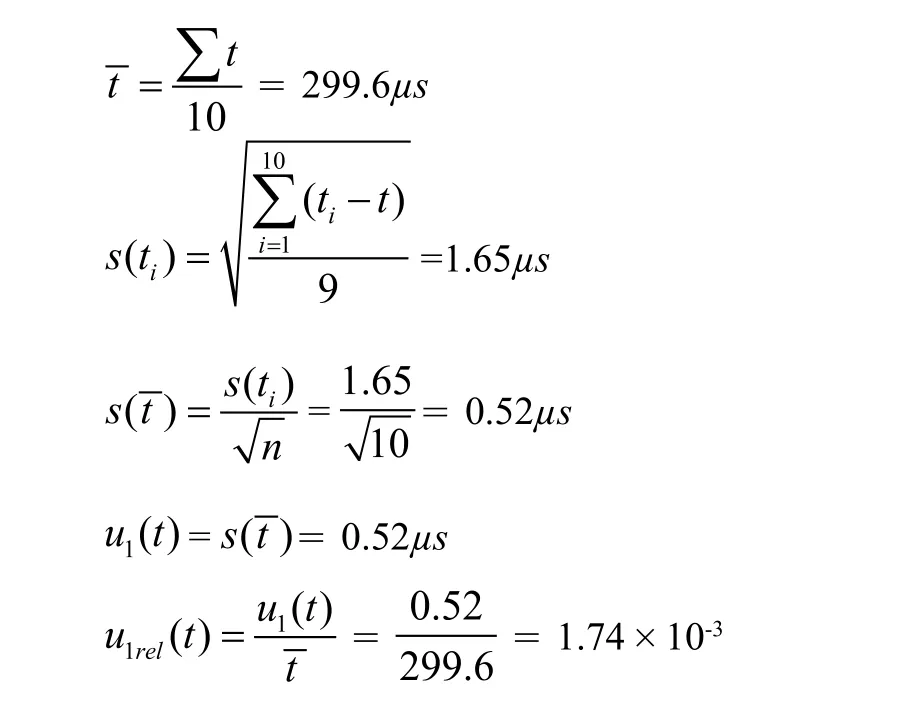
② 测量误差引入的B类不确定度
用数字示波器测量脉冲宽度时,取样间隔=扫描时间/格÷250,测量误差a=取样间隔+100ppm读数=50µs÷250+0.01%×299.8µs =0.23µs,属矩形(均匀)分布,k =
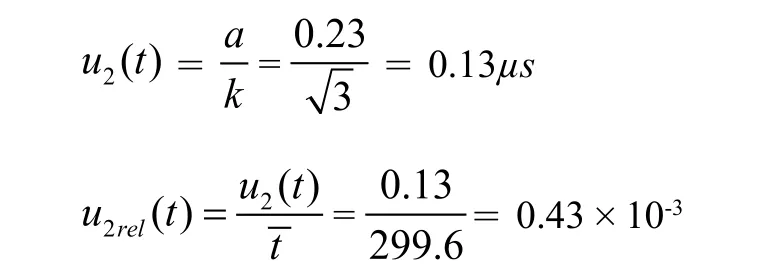
③ 分辨力引起的B类不确定度
数字示波器测量脉冲宽度的分辨力为1µs,数字示值分散区间半宽,即0.5µs,并取均匀分布,其标准不确定度为:


B类不确定度大都有严格数据关系,因此自由度为∞。根据不确定度的计算关系,在实际测量中,若该输入量测量的离散性大,误差大,灵敏度系数高,则对合成不确定度的影响就大,数据的权重就高,即主要决定了合成不确定度的最终结果。若该输入量测量的一致性好,误差小,灵敏度系数低,则对合成不确定度的影响就小,数据的权重就低,即可以忽略不计。
在实际测量时,由于计量检定中不确定度的读数重复性和实际测量的读数重复性并没有必然联系(即使数据一致,引入计量检定读数重复性的不确定度也会造成实际测量的重复计算),且计量检定中溯源检定仪器的测量误差、分辨力也不应移植到测量仪器上,所以计量检定证书的不确定度不应计入实际测量不确定度的计算过程。如果计量检定改变了某个测量仪器的测量误差,则按发生改变的测量误差进行不确定度的测量和计算。当某个输入量(如电阻)的校准证书已经给出了不确定度,则可以直接用于计算,不必进行重复的不确定度测量和计算过程。(5) 扩展不确定度
根据合成不确定度的自由度计算结果,截断尾数
得= 50
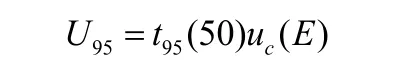
为保证规定的置信度,当计算出的合成不确定度的自由度有尾数时,应截断尾数,按较小的自由度值查t分布表选取对应较大的数据涵盖区间。
根据JJF1059《测量不确定度评定与表示》,查t分布表得

脉冲输出能量的不确定度报告
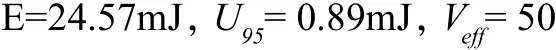
5 结束语
测量不确定度已越来越受到国际上的普遍重视,不确定度的评定和表示,也可以极大的统一理解和说明测量结果。在我们目前的检测、检验以及相关的业务中,包括校准证书、检定证书、测试报告、学术报告、技术规范、产品标准及合同协议书等文件都要求使用有关测量结果和测量不确定度的表述,而在质量管理和质量保证的系列文件中也规定应保证所用设备的测量不确定度都是已知的。因此,在工作中需加强对测量不确定度的研究和应用,以提高检测、检验水平,从而更好地能够与国内外测量要求统一起来。 ■
Uncertainty of the Opinion
ZHANG Zhi-qing
ShanXi Center for Medical Devices Testing (Taiyuan 030012)
Uncertainty is an internationally recognized quality measurement used to assess the parameters, is to report the scale of measurement. Accurate and reasonable evaluation, is to provide accurate measurements of the premise and guarantee, Uncertainty This paper discusses the content and to low frequency pulse output energy of the treatment apparatus of Uncertainty example, analysis the uncertainty of the process and methods.
uncertainty, error of measurement, degrees of freedom, coverage factor
1006-6586(2010)08-0040-07
R197.39
A
2010-05-04
张志清,室主任
