相位法及其在阵列声波测井中的应用
2010-09-14任跃廷沈建国夏克文张存善
任跃廷沈建国夏克文张存善
(1.河北工业大学信息工程学院 天津) (2.天津大学 天津)
相位法及其在阵列声波测井中的应用
任跃廷1沈建国2夏克文1张存善1
(1.河北工业大学信息工程学院 天津) (2.天津大学 天津)
由于首波衰减,频散效应的影响,用阈值法处理声波测井波形所得到的时差会有一定的误差。文章给出了处理阵列声波测井波形的相位法,并用该方法处理了实际测井波形,与普通声波、express处理结果分别进行了对比。对比结果表明:相位法处理的声波时差分辨率较高,分层比较明显。
阵列声波测井;频率特性;相位法
0 引 言
声波测井仪测量地层的声波时差。声波时差反应地层的纵波传播速度。根据不同岩层和流体中的声波传播速度,可以进行储集层的岩性辨别,孔隙度计算等。声波测井波列包含多种声波信号。从几何声学上分有滑行纵波、滑行横波、直达波、井壁反射波。从物理声学上分有纵波、横波、斯通利波、伪瑞利波等。通常情况下,普通声波测井仪利用阈值法计算纵波时差。但理论计算表明首波幅度随源距衰减很快,源距为1.5 m时接收波形的首波已经无法识别,这样用阈值法计算时,由于首波位置无法准确判别,计算的时差值就会有一定的误差。
而且接收波形在一定频率范围内有频散现象[1],这种现象会导致首波的形状发生改变,这时用阈值法得到的时差也会有一定的误差。声波测井仪接收探头的间距一般较短,为保证这类仪器的测量精度,就要求从波形上读取的时间误差尽量小,因此考虑频散效应的影响也就显得更为重要。
本文提出的相位法在频域进行计算。它有效地去除了频散的影响,能够得到精确度较高的纵波时差曲线。该方法还可以在频域内有效地分离纵波、横波和斯通利波,分别得到这些波的时差。
1 常规声波测井面临的问题
常规声波测井仪计算纵波时差时利用阈值法。该方法成立的基本假设是:滑行纵波在传播过程中的速度等于地层纵波速度,相位固定,不随源距变化。阈值法在计算时首先设定一个阈值,当波的幅度超过此值时认为发射探头发射的声振动到达该接收探头处。由不同源距接收探头接收到声振动的时间差除以两接收探头间的距离就得到纵波时差(Δt/Δz)。
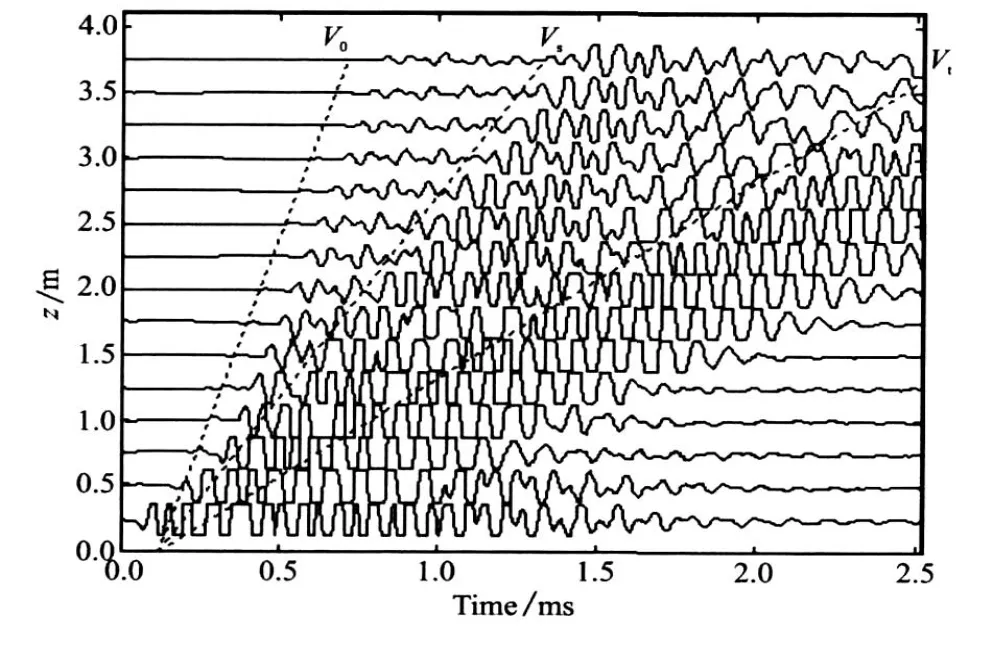
图1 不同源距接收波的理论计算波形
图1 是一组不同源距接收波的理论计算波形。由图可见,源距为1.4m时,接收波的首波已经无法识别。在用1.4m源距和其他任意近源距接收波计算时差时,因1.4m源距接收波的首波难以识别,从而造成时差的计算结果偏大。目前国内常用的声波测井仪的源距分别是:0.915m、1.12m、1.32m、1.52m 和0.915m、1.06m、1.21m、1.51m。在不同源距的接收波中很可能出现近源距接收波有首波,远源距接收波首波衰减严重的情况。这时计算出的时差就会有很大误差。
测量波形中纵波的速度频散特征将导致首波的形状发生改变,影响首波的相位[1],用阈值法计算的声波时差会有一定的误差。当两个相邻接收探头接收到的首波时间差误差为2μs时,时差值的误差就会在10 μs左右甚至更大。所以只有精确计算两列接收波形首波的时间差,才能保证时差的测量精度。
仅仅从波列中提取纵波时差已经不能满足现代石油测井的需求。在得出纵波时差的基础上,人们还希望得到横波时差、斯通利波时差等测井资料以更准确的判断储集层信息。利用相位法,不仅能从波列中更精确的提取纵波时差还可以得到横波和斯通利波时差。
2 相位法原理
用相位分析方法研究声波测井波形的处理方法起源于直接相位法[2]。除了对纵、横波的相位差进行补偿以外,直接相位法还可以用两个源距测量波形的相位差识别全波波形中的横波。直接相位法主要是针对两个源距的声波测井波形的,而阵列声波测井有8个或更多接收波形。这时,直接相位法需要作相应的改进。
我们首先讨论测量波形中只有一个声波f1的情况,其速度随频率变化,忽略噪声影响,则有f(t,z)=f1(t-s1z)对 f进行Fourier变换得到[3]:
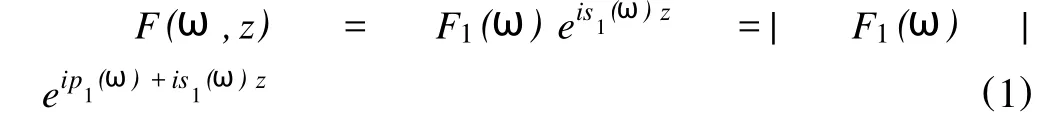
式中,p1(ω)是 F1(ω)的相位。从式(1)可以看到:速度随频率的变化关系包含在相位信息当中或者说是以相位的形式出现的。
当有N个位于不同位置Zn(1,2,…,N)的接收波形时,每个接收波形的Fourier变换为:
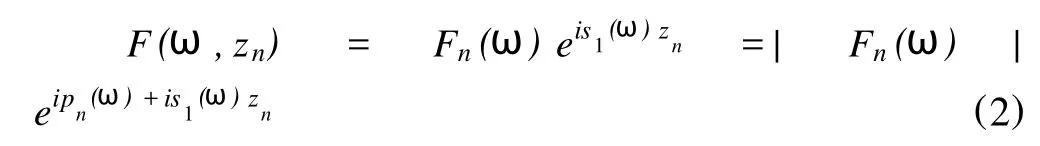
式(2)中,zn=z0+ndz。对于固定的频率ω=ωq,Pn(ωq)和 s1(ωq)是常数,当探头的一致性比较好(pn(ωq)=pn(ωq)= …pn(ωq))时,相位中随距离改变的部分为s1(ωq)zn,这是一个关于z的线性函数,其斜率为所要计算的慢度 s1(ωq)。即:对于固定角频率ω、探头比较一致的情况下,从式(2)可以看出:如果以z为横坐标,不同位置探头声波波形的相位为纵坐标,相位点的分布应该是一条直线。由这条直线的斜率即可得到该频率分量的相位变化Δφ,进而得到该频率分量的声波时差。当接收波中有多个模式波时,各个波的情况与只有一个波时类似。
相位法计算接收波形中所有频率分量的时差值,并对这些时差值进行综合处理得到时差分布曲线。纵波、横波、斯通利波在频域特性和时差值上都有较大的差异,利用这些差异,就可以在频域将它们分离,在时差分布曲线上形成不同的峰值。然后根据时差分布曲线的峰值得到各自的时差。
3 相位法处理结果
利用相位法处理声波测井资料不仅能够得到精度较高的纵波时差,而且能较容易的从全波资料中提取横波、斯通利波时差。利用相位法阵列声波处理软件,我们对多口井实际测井资料进行了处理。
3.1 相位法处理的纵波时差
相位法处理的纵波时差与普通声波对比如图2所示,图2中,右侧是用相位法处理出来的时差分布图,浅色表示时差在该处分布最为集中,浅色分布图中的黑线是根据时差分布的最大值得到的,代表地层的纵波时差曲线。将该纵波时差曲线绘制在左图中(见深色曲线),与浅色曲线(阈值法得到的声波时差)对比发现:两者的一致性和差别是非常明显的。

图2 相位法处理的纵波时差与普通声波对比
在1806m~1812m,两种方法所处理的时差一致性比较好,基本上能够重合。测量波形中首波幅度比较大,地层的物理衰减比较小,用阈值法处理时所用到的首波是同一个(没有出现近源距接收波形首波衰减小,远源距接收波形首波衰减剧烈的情况),也没有频散影响,测量的时差是比较精确的。在1812m~1 815m井段,两者差异较为明显,相位方法处理的声波时差分层比较清楚、时差精度比较高。
3.2 相位法处理的横波、斯通利波时差
相位法处理的横波、斯通利波时差如图3所示,图3(1)是相位法的处理界面,该界面上的3幅图中,上面的图是原始测井波形,中间图是频域的分离结果。从该图可以发现:相位法可以很好的将波形中的纵波、横波、斯通利波在频域内分离。用这些分离的时差分布可以得到最下面的时差分布曲线。将时差分布曲线用颜色表示,并且将各点连续绘图得到图3(2)右侧的声波成像图。将这些成像曲线中最大值位置取出得到时差曲线。3(2)中左图是用相位法提取的纵波、横波、斯通利波时差曲线与5700express软件处理的时差曲线的对比。与纵波时差的处理结果相似,相位法处理的声波时差分辨率比较高,分层比较明显。
4 结 论
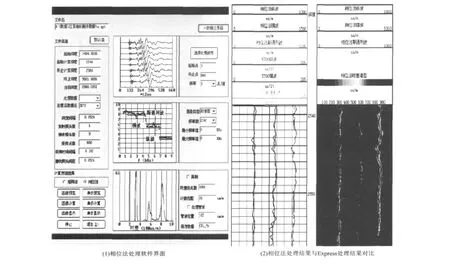
图3 相位法处理横波、斯通利波时差
相位法从方法层面上消除了声波波形频散的影响,减小或者基本消除了滑行波幅度小、随源距衰减大等因素的影响,得到了精度比较高的纵、横波时差。同时,在频域内很好地将横波、斯通利波等其他模式波分离。在阵列声波测井波形数据的处理中有较好的应用前景。
[1] 沈建国,任月娥,张宏敏.高分辨率声波测井面临的问题及其对策[J].石油地球物理勘探,2006,41(1)
[2] J.D.Ingram.etal.DirectphasedeterminationofS-wave velocitiesfromacousticwaveformlogs,Geophysics,1985,50(11)
[3] 沈建国.应用声学基础——实轴积分法及二维谱技术[M].天津:天津大学出版社,2004
P631.8+1
B
1004-9134(2010)02-0052-03
2009-10-14 编辑:高红霞)
任跃廷,男,1983年生,河北工业大学在读硕士研究生,专业:微电子学与固体电子学。邮编:300130
