基于抗差K alman滤波的精密单点定位

聂建亮,张双成,徐永胜,张玉芳,王月莉

(1.国家测绘局大地测量数据处理中心,陕西西安 710054;2.长安大学地质工程与测绘学院,陕西西安 710054; 3.长安大学测绘新技术研究院,陕西西安 710054;4.国家测绘局第一航测遥感院,陕西西安 710054)

基于抗差K alman滤波的精密单点定位

聂建亮1,2,张双成2,徐永胜3,张玉芳4,王月莉4

(1.国家测绘局大地测量数据处理中心,陕西西安 710054;2.长安大学地质工程与测绘学院,陕西西安 710054; 3.长安大学测绘新技术研究院,陕西西安 710054;4.国家测绘局第一航测遥感院,陕西西安 710054)

当精密单点定位的观测值含有异常数据时,Kalman滤波的精度将会降低。采用抗差Kalman滤波方法能够有效抑制观测异常,提高滤波的精度和可靠性。运用武汉国际GPS服务跟踪站数据对该方法进行了验证。结果表明,抗差Kalman滤波的精度比Kalman滤波的精度有一定程度提高,说明抗差Kalman滤波能够有效抑制观测异常。

精密单点定位;抗差Kalman滤波;等价权

0 引言

自从1997年Zumberge等[1]提出了精密单点定位方法以来,精密单点定位得到快速发展。国内外学者对该定位方法进行了深入研究,并编制了相应的定位软件[2-6]。可靠的Kalman滤波算法要求可靠的函数模型。可靠的函数模型是指物理运动方程以及观测方程能精确地表征物理和几何现实[7]。在GPS观测过程中,观测值难免会出现异常数据,目前虽然可以采取措施探测修复周跳,但对于小周跳来说,探测与修复仍然比较困难;由于某些原因,观测值可能出现粗差,目前可以采用探测、诊断、修复方法,即DIA方法[8-10],但计算复杂。针对这些问题,精密单点定位采用抗差Kalman滤波[11-12],该方法可以有效地抑制观测异常,提高精密单点定位的精度和可靠性。

1 精密单点定位模型

为了达到分米级甚至厘米级定位精度,文献[13]指出了精密单点定位的4个关键之处。针对精密单点定位的关键问题,笔者采用伪距和载波观测值;为了得到高精度的卫星轨道和卫星钟差,采用国际GPS服务(International GPS Service,IGS)提供的精密星历和精密钟差;对于其他影响因素,分别采取模型改正。

传统精密单点定位的伪距与载波的非差观测方程为

对于对流层、电离层等误差项,分别采用模型或改正项进行削弱。其中,对流层延迟可以采用Saastamoinen[14]或Hopfield[15]等模型改正;采用无电离层组合观测值消除电离层一阶项的影响;固体潮与海潮采用模型进行改正。

在定位计算之前,首先要进行周跳探测与修复工作。单点定位仅仅采用单个测站数据,无法使用常规方法探测与修复周跳。在精密单点定位中,通常采用双频双P码组合观测值修复周跳,其中,组合观测值有M-W组合、消电离层组合、Geometryfree组合[16]。虽然这些方法能够很好地修复大周跳,但很难有效地修复小周跳。

2 抗差Kalman滤波

第k历元Kalman滤波的动力学方程与观测方程为

式中:Φk,k-1为状态转移矩阵;Lk为第k历元的观测向量;Xk-1、Xk分别为第k-1、k历元的状态向量; Ak为观测方程系数矩阵;Wk为状态噪声;ek为观测噪声。

式中:Kk为增益矩阵;为单位权中误差,为等价权矩阵;为预报值及其对应的协方差矩阵;I为单位阵。

式中:k0、k1分别为1.2、3.0为第i个观测值的标准化残差;pii为权元素。该方案对观测值的权分3种情况进行处理,即当观测值服从正态分布时,权保持不变;当观测值超出一定范围时,采用降权处理;当个别观测值明显异常时,采用零权处理。IGGⅢ方案对观测值降权处理可以有效抑制观测异常,提高观测精度。

在精密单点定位中,载波与伪距的测量精度比大约为1∶100;因此,笔者尝试只对载波观测值的权进行等价权处理。另外,采用IGGⅢ方案计算等价权。

3 算例分析

本算例数据来源于2006年1月6日武汉IGS跟踪站的GPS观测数据,数据采样间隔30 s。为了分析各种方案的可靠性,算例采用IGS提供的坐标作为“真值”,将计算结果与“真值”作差进行比较。位置、钟差、模糊度、载波和伪距观测值的初始方差分别为1、900、1.0×1010、4.0×10-6、4.0× 10-4m2。采用3个方案进行计算分析:①标准Kalman滤波(KF);②抗差Kalman滤波,采用载波观测残差,仅对载波观测值进行降权(RKF1);③抗差Kalman滤波,等价权为IGGⅢ方案(RKF2)。

图1～3为3种方案分别在北、东、天顶方向误差图;表1为北、东、天顶方向误差统计结果。

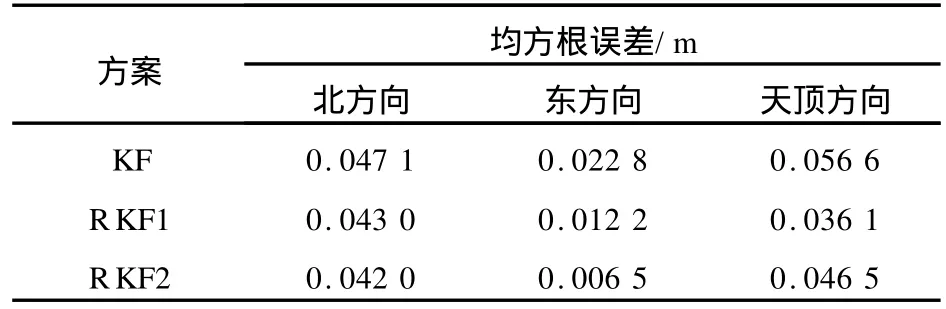
表1 各方案北、东、天顶方向误差统计结果Tab.1 Statistical Results of North,East, Zenith Axises of Schemes

由算例分析可以得出如下认识:

(1)在各项误差得到改正以及观测数据为“干净”数据的前提下,Kalman滤波处理精密单点定位数据可以达到厘米级甚至更高的精度。

图1 各方案北方向误差曲线Fig.1 Errors of North Axis of Schemes

图2 各方案东方向误差曲线Fig.2 Errors of East Axis of Schemes

图3 各方案天顶方向误差曲线Fig.3 Errors of Zenith Axis of Schemes

(2)若观测数据存在异常,两种抗差Kalman滤波方案能够有效地抑制观测数据中观测异常的影响,提高精密单点定位的精度。

4 结语

对于静态GPS数据处理,Kalman滤波是一种非常有效的方法。但是,当观测数据中存在异常数据时,Kalman滤波精度将会大大降低,甚至出现滤波发散。抗差Kalman滤波则通过降低异常观测数据的权,有效抑制了观测异常对计算结果的影响,提高滤波的精度和可靠性。另外,对于动态精密单点定位,载体机动和观测异常都是影响滤波精度的重要因素;因此,下一步研究需要合理地构造自适应因子以及抗差自适应滤波在动态精密单点定位的应用。

[1] Zumberge J F,Heflin M B,Jefferson D C,et al.Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J].Journal ofGeophysical Research,1997,102(B3):5005-5017.

[2] Gao Y.Canadian High Precision Real-time GPS Correction Service and Real-time Atmosphere and Deformation Monitoring[R].Wuhan:CPGPS Workshop,2008.

[3] Abdel-Salam M.Precise Point Positioning Using Undifferenced Code and Carrier Phase Observations[D].Calgary:The University of Calgary,2005.

[4] Witchayangkoon B.Element of GPS Precise Point Positioning [D].Orono:The University of Maine,2000.

[5] 叶世榕.GPS非差相位精密单点定位理论与实现[D].武汉:武汉大学,2002.

[6] 张小红,刘经南,Forsberg R.基于精密单点定位技术的航空测量应用实践[J].武汉大学学报:信息科学版,2006,31(1): 19-22.

[7] 高为广.自适应融合导航理论与方法及其在GPS和INS中的应用[D].郑州:解放军信息工程大学,2005.

[8] Teunissen P J G,Salzmann M A.A Recursive Slippage Test for Use in State-space Filtering[J].Manuscripta Geodaetica, 1989,14(6):383-390.

[9] Teunissen P J G.Quality Control in Integrated Navigation Systems[J].IEEE Aerospace and Electronic Systems Magazine,1990,5(7):35-41.

[10] Salzmann M.Real-time Adaptation for Model Errors in Dynamic Systems[J].Bulletin Geodesigue,1995,69(2):81-91.

[11] 杨元喜.动态系统的抗差Kalman滤波[J].解放军测绘学院学报,1997,14(2):79-84.

[12] 杨元喜.自适应动态导航定位[M].北京:测绘出版社,2006.

[13] 刘经南,叶世榕.GPS非差相位精密单点定位技术探讨[J].武汉大学学报:信息科学版,2002,27(3):234-240.

[14] Saastamoinen J.Contributions to the Theory of Atmospheric Refraction[J].Bulletin Geodesique,1972,105(1):279-298.

[15] Hopfield H S.Two-quartic Tropospheric Refractivity Profile for Correcting Satellite Data[J].Journal ofGeophysical Research,1969,74(18):4487-4499.

[16] Blewitt G.An Automatic Editing Algorithm for GPS Data [J].Geophysical Research Letters,1990,17(3):199-202.

[17] 杨元喜.抗差估计理论及其应用[M].北京:八一出版社,1993.

[18] 聂建亮,吴富梅.Kalman滤波几种异常检验法[J].地球科学与环境学报,2008,30(2):204-208.

Precise Point Positioning Based on Robust K alman Filtering

NIEJian-liang1,2,ZHANG Shuang-cheng2,XU Yong-sheng3,ZHANG Yu-fang4,W ANG Yue-li4

(1.Geodetic Data Processing Center,State Bureau of Surveying and Mapping,Xi'an710054,Shaanxi,China;2.School of Geological Engineering and Surveying,Chang'an University,Xi'an710054,Shaanxi,China;3.Institute of New Surveying Research,Chang'an University,Xi'an710054,Shaanxi,China;4.The First Institute of Photogrammetry and Remote Sensing,State Bureau of Surveying and Mapping,Xi'an710054,Shaanxi,China)

If the outliers exist in the observations,the accuracy of Kalman filtering will be lower.Robust Kalman filtering,which can improve the precision and the reliability of Kalman filtering,is used to control the outliers. The data from the tracking station of International GPS service in Wuhan are computed to test the efficiency of Robust Kalman filtering.The results show that the precision of Robust Kalman filtering is better than Kalman filtering,and it can control efficiently outliers in the observations.

precise point positioning;Robust Kalman filtering;equivalent weight

P207+1

A

1672-6561(2010)02-0218-03

2009-07-01

国家自然科学基金项目(40774001)

聂建亮(1979-),男,河南新乡人,工学博士研究生,从事测量数据处理研究。E-mail:niejianliang@163.com