云母石英片岩蠕变模型参数选择研究

陈文玲,赵法锁

(1.长安大学地质工程与测绘学院,陕西西安 710054;2.长安大学西部矿产资源与地质工程教育部重点实验室,陕西西安 710054;3.长安大学岩土工程开放研究国土资源部重点实验室,陕西西安 710054)

云母石英片岩蠕变模型参数选择研究

陈文玲1,2,3,赵法锁1,2,3

(1.长安大学地质工程与测绘学院,陕西西安 710054;2.长安大学西部矿产资源与地质工程教育部重点实验室,陕西西安 710054;3.长安大学岩土工程开放研究国土资源部重点实验室,陕西西安 710054)

根据三轴蠕变试验曲线的特点,建立了云母石英片岩七元件线性黏弹塑性蠕变模型,采用最小二乘法对蠕变柔量-时间曲线和应变-时间蠕变曲线进行拟合确定蠕变模型参数,讨论了确定蠕变模型参数的影响因素及参数的合理性与可用性。结果表明:由于受到分级加载次数、初次加载应力值和加载时间的影响,两种曲线拟合确定的参数各不相同;云母石英片岩蠕变模型的非线性较明显;蠕变柔量-时间曲线拟合确定的参数不予采用,应变-时间蠕变曲线拟合确定的参数在各级应力水平下变化规律不明显;采用某种单一方法确定蠕变模型参数不够全面,建议采用综合辨识法,这样才能保证岩土工程中蠕变数值分析结果的正确合理性以及施工设计的安全可靠性。

线性;黏弹;塑性;蠕变模型;参数;综合辨识法

0 引言

随着功能强大的大型专业岩土工程数值计算软件的出现,数值计算对工程的仿真能力越来越强,计算结果的可靠性主要取决于岩土体本构模型和输入参数的正确性。岩土体本构模型和参数辨识是岩土力学理论与工程实践中的两大研究课题,也是架构理论联系实际的桥梁。目前,材料参数的确定方法可分为经验类比法、直接试验方法、原型观测反分析法等。近年来,随着计算技术的发展,工程界涌现出一些新的参数反分析方法,如灰色系统理论、人工神经网络技术、遗传进化算法[1]等。根据室内试验数据及曲线确定岩石蠕变参数的方法主要有最小二乘法[2-4]、回归分析法[5]、优化分离法[6-7]以及曲线分解法[8]等,其本质是用不同的数学方法对试验曲线进行拟合。其中,最小二乘法是应用最为广泛的一种方法,精度较高。已有的文献中,由最小二乘法来确定线性黏弹塑性模型参数的常用方法主要有2种:①对蠕变柔量-时间曲线进行拟合确定参数;②对应变-时间蠕变曲线进行拟合确定参数。

笔者首先根据三轴蠕变试验结果建立了云母石英片岩线性黏弹塑性蠕变模型,然后用2种常用方法对蠕变模型参数进行了拟合,并对其结果进行分析讨论。

1 线性黏弹塑性蠕变模型的建立

1.1 三轴蠕变试验曲线

云母石英片岩是一种软弱变质岩,呈灰黑-暗灰色,片理较为发育,云母片多沿片理面分布,云母石英片岩力学性质具有明显的各向异性,当轴向应力加载方向不同时,试验结果不一样。采用分级加载方式对云母石英片岩进行三轴蠕变试验,所用仪器为RLW-2000岩石三轴蠕变试验机,施加围压为2 MPa,试验中轴向应力加载方向垂直于片理方向,施加的应力水平分别为15、20、25、50、52.5 MPa,分级加载直至试件破坏,破坏应力为52.5 MPa。试验所得云母石英片岩三轴蠕变试验曲线见图1。图1中轴向蠕变在发生瞬时变形后可划分为衰减蠕变阶段、等速蠕变阶段和加速蠕变阶段。当轴向力小于破坏应力时,只有前两个阶段的蠕变,只有当轴向力加至大于破坏应力时,才出现加速蠕变阶段。

1.2 线性黏弹塑性蠕变模型的建立

当应力水平较低时,云母石英片岩具有瞬时弹性和衰减稳定的蠕变特性,可以用广义Kelvin模型来描述。广义Kelvin模型由一个虎克元件与多个Kelvin元件串联组成。其蠕变方程为

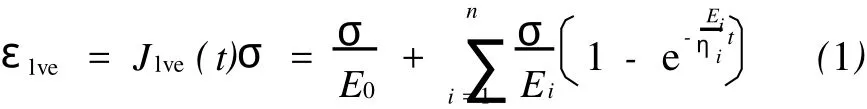
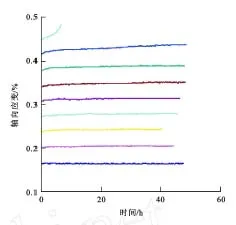
图1 分级加载条件下岩石三轴蠕变试验曲线Fig.1 Triaxial Creep Curve of Rock After Rating Load

式中:εlve为线性黏弹性应变;σ为加载应力;t为加载时间;Jlve(t)为线性黏弹性蠕变柔量;E0为虎克元件的弹性模量;Ei和ηi分别为第i个Kelvin元件的弹性模量和黏滞系数。

在广义Kelvin模型中,串联着不同数目Kelvin元件的模型虽都描述瞬时弹性和衰减稳定蠕变,而且最终蠕变稳定值也都一样,但对蠕变发展较快的开始阶段描述的精确程度不同,即串联的Kelvin元件个数N越多,广义模型所描述的蠕变曲线越逼近实际的蠕变特性,但是,却带来了模型中待定参数增多的问题,给实际应用带来较大不便,所以,在选择Kelvin元件个数N时,既要考虑能比较准确地反映岩土体的实际蠕变特性,又要使模型中的待定参数尽可能地少。借鉴以往经验,取N=2时,一般可以满足应用[9]。这里选用五元件Kelvin模型来描述云母石英片岩的黏弹性蠕变规律。当N =2时,原蠕变方程变为

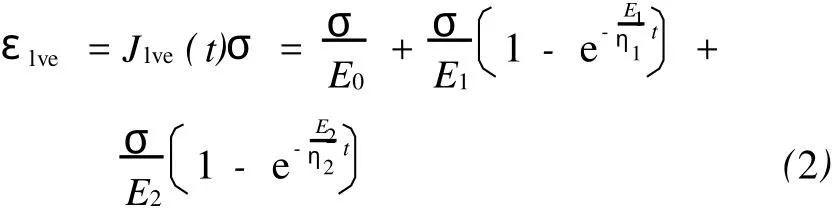
式中:E1和η1分别为第1个Kelvin元件的弹性模量和黏滞系数;E2和η2分别为第2个Kelvin元件的弹性模量和黏滞系数。

此时的线性黏弹性蠕变柔量为

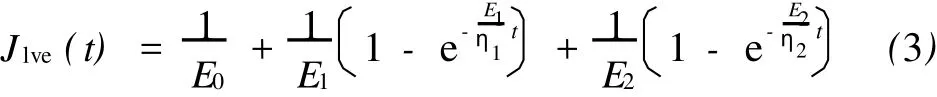
在应力水平较高时,大于某一应力时,出现等速蠕变阶段,可以用黏性元件和塑性元件并联组成的黏塑性体来描述云母石英片岩的黏塑性蠕变规律。其蠕变方程为

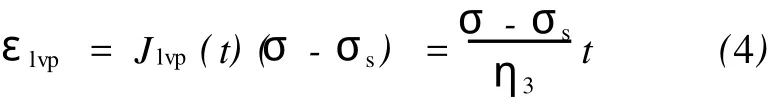
式中:εlvp为线性黏塑性应变;σs为屈服应力;Jlvp为线性黏塑性蠕变柔量;η3为第3个Kelvin元件的黏滞系数。

此时的线性黏塑性蠕变柔量Jlvp(t)为

将黏弹性阶段蠕变模型和黏塑性阶段蠕变模型组合在一起,得到云母石英片岩的黏弹塑性蠕变模型(图2)。

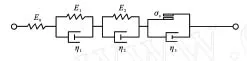
图2 云母石英片岩的线性黏弹塑性蠕变模型Fig.2 Linear Viscoelastic Plastic Creep Model of Mica-quartzose Schist

结合式(2)、(4)可得云母石英片岩的线性黏弹塑性蠕变模型的本构关系

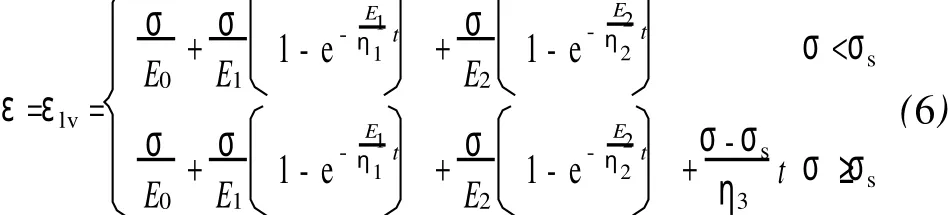
式中:ε、εlv为线性黏弹塑性应变。

2 模型参数拟合

2.1 拟合软件

精确可靠的技术方法对蠕变模型的选择、参数识别以及拟合曲线与试验资料的吻合等都至关重要[10]。进行参数求解时,最小二乘法在许多有效的参数估计法中一直占统治地位[11],然而,该法仍无法避免参数初始值难于选择的困难。为克服这一缺点,有学者进行改进,提出改进的最小二乘法[12],基于模式搜索的岩石蠕变模型参数识别[13]。采用拟合软件1stOpt,其最大特点是,在绝大多数情况下,不需要使用者提供(猜测)任何初始值,仅依靠自身的全局搜索能力,从任意随机值出发,既可求得最优解。实际应用中选择确定合理的初始值组是一件非常困难的事,尤其是在参数量比较多的情况下;因此,1stOpt已为业界所公认。

2.2 拟合结果

用2种常用方法对蠕变模型参数进行了拟合。

2.2.1 方法1:对蠕变柔量-时间曲线拟合确定参数

以屈服应力σs为分界点,将等时应力应变曲线分为黏弹性阶段和黏塑性阶段。

(1)确定黏弹性阶段的模型参数。考虑初始条件t=0时,E0=σ/ε,则E0即为瞬时弹性模量,也就是云母石英片岩等时应力应变曲线的黏弹性阶段在t=0时的斜率值,可直接确定。

由等时应力应变曲线黏弹性阶段的斜率可得云母石英片岩在不同时刻的线性黏弹性模量Elve(t),由此可得到线性黏弹性模量Elve(t)随时间变化的规律。线性黏弹性蠕变柔量Jlve(t)和线性黏弹性模量Elve(t)互为导数关系,即

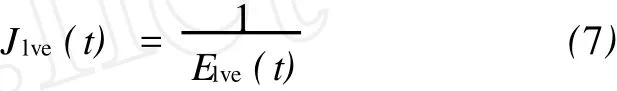
进而得到线性黏弹性蠕变柔量Jlve(t)随时间变化的规律。利用数据处理软件对云母石英片岩Jlve(t)—t曲线数据进行拟合,由此来确定模型参数。

(2)确定黏塑性阶段的模型参数。当云母石英片岩的蠕变应力σ大于屈服应力σs时,云母石英片岩的蠕变表现出黏塑性特点,由等时应力应变曲线的黏塑性阶段得到黏塑性应变与过应力(σ-σs)等时曲线,再由黏塑性应变与过应力(σ-σs)等时曲线的斜率得到在不同时刻的线性黏塑性模量Elvp(t),由此可得到线性黏塑性模量Elvp(t)随时间变化的规律。线性黏塑性蠕变柔量Jlvp(t)和线性黏塑性模量Elvp(t)互为导数关系,进而得到线性黏塑性蠕变柔量Jlvp(t)随时间变化的规律,Jlvp(t)—t曲线斜率的倒数即为η3。这样确定的模型参数在不同应力水平下是一样的。

该方法的结果见表1。图3、4分别为Jlve(t)—t曲线和Jlvp(t)—t曲线。该方法的实质是将岩土材料简化为理想的线性黏弹塑性体,在黏弹性阶段,这种简化和云母石英片岩试验特性接近,所以在图3中试验值和拟合曲线吻合较好;在黏塑性阶段,这种简化和云母石英片岩试验特性相差较大,所以在图4中试验值和拟合曲线差别较大。

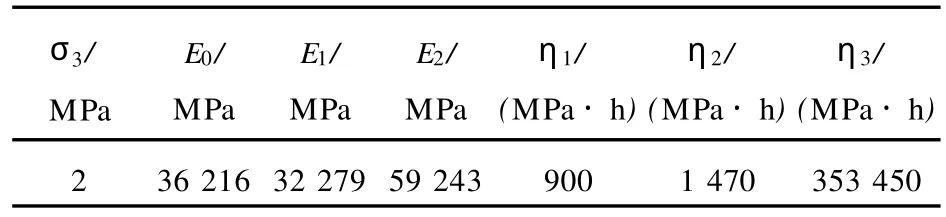
表1 对蠕变柔量-时间曲线拟合确定的模型参数Tab.1 Model Parameters Which were Fixed by the Fitting of Creep Compliance-time Curve

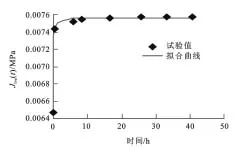
图3 黏弹性蠕变柔量与时间的关系Fig.3 Relationship ofJlve(t)to Time

图4 黏塑性蠕变柔量与时间的关系Fig.4 Relationship ofJlvp(t)to Time

2.2.2 方法2:对应变-时间蠕变曲线拟合确定参数

利用数据处理软件对云母石英片岩的轴向应变-时间蠕变曲线数据进行拟合,由此来确定模型参数。

这样确定的模型参数在不同的应力水平下是不同的,可以分析模型参数随应力水平的变化,最后可以取各级应力水平模型参数的平均值作为模型参数(表2)。2.3 拟合结果分析

表2 对应变-时间蠕变曲线拟合确定的模型参数Tab.2 Model Parameters Which were Fixed by the Fitting of Creep Strain-time Curve

表1、2中模型参数是根据以下4点来确定:相关系数大于0.8;实时观察拟合曲线和试验曲线的吻合情况;考虑试验曲线的发展趋势;不同应力水平下模型参数的理论变化趋势。

上述由试验曲线拟合求模型参数的2种方法,拟合所得模型参数受以下影响:①分级加载次数:所分级加载次数越多,后面级数的模型参数受前面级数的累计影响越大;②初次加载应力值:初次加载应力值越大,在试验所得蠕变曲线中,只具有衰减蠕变阶段的蠕变曲线就越少;③加载时间:加载时间越长,越能真实反映蠕变曲线的发展趋势。

对拟合结果进行分析比较,得出如下认识:

(1)2种方法得到的线性黏弹塑性蠕变模型参数各不相同。

(2)对比表1、2中各模型参数,两者相差较大,表明云母石英片岩蠕变的非线性较明显。方法1实质上是将岩土材料简化为理想的线性黏弹塑性体,即认为蠕变柔量仅仅是时间的函数,而与应力水平无关,故求得的模型参数唯一。方法2每级应力水平对应求出一组模型参数,如果各级应力水平下求得的模型参数相同,则表明所研究岩土材料为理想的线性黏弹塑性体,不同则表明所研究岩土材料为非线性黏弹塑性体,即蠕变柔量不仅是时间的函数,还与应力水平有关。因此,如果方法1、2的模型参数相差越小,则表明云母石英片岩蠕变的非线性不明显,反之,则蠕变的非线性明显。对比表1、2中各模型参数,两者相差较大,表明云母石英片岩蠕变的非线性较明显。从表2中可以看出,不同应力水平的模型参数相差较大,且应力水平越高,相邻应力水平的模型参数相差越大,拟合相关系数基本上也随着应力水平的增大而变越小,特别是出现等速蠕变阶段后相关系数明显变小,这同样表明云母石英片岩为非线性黏弹塑性体。

(3)方法1所得模型参数不予采用。方法1是由等时应力应变曲线间接得到,又对等时应力应变曲线做了线性简化,其结果和蠕变曲线的实际吻合情况肯定比方法2要差,而方法1和方法2的模型参数相差较大,故方法1可以不采用。

(4)方法2得到的模型参数在各级应力水平下变化规律不明显。因为云母石英片岩的黏弹塑性变形是非线性的,非线性拟合程序是按最小二乘法的原则设计,不同的参数组合都可实现试验数据与拟合数据距离平方和最小的原则,虽然在拟合过程中考虑到不同应力水平下模型参数的理论变化趋势,但仍未得到理想结果。同时分级加载方式下,后面级数的模型参数受前面级数的累计影响大。如果采用分别加载方式,并且每个应力级平行测试2～3个岩石样品,取其平均值,变化规律可能会更明显。但这种理想试验方式耗时费资,并不可取。李青麟[10]、陈炳瑞[13]认为,实际上岩石流变参数在不同应力条件下并非定值,确定流变参数时,理论上应将岩石应力作为参数变量进行类似计算,以确定流变参数与应力水平的函数关系。目前对这种关系的研究还不多,同时,考虑到工程实践中岩体条件的复杂性,岩石力学试验中尚存在不确定因素;因此,强调不同应力水平下流变参数的差异并不一定能够提高计算精度,在进行流变分析时,仍假定在各级荷载下岩石流变参数均保持常数。

3 结语

(1)对于同一个试验结果,采用2种不同的拟合方法,得到的云母石英片岩线性黏弹塑性蠕变模型参数不同。

(2)由于受到分级加载次数、初次加载应力值和加载时间的影响,所以对同一个云母石英片岩试件,当试验过程不同时,拟合所得到的线性黏弹塑性蠕变模型参数不同。

(3)单一采用某种方法确定蠕变模型参数不够全面,建议采用综合研究评判的办法进行蠕变模型参数选择。可按如下步骤进行:①试验研究+经验类比+反分析,初步确定蠕变模型参数;②结合蠕变的影响因素分析,对蠕变模型参数进行综合分析、评判、调整;③重复前面两步骤;④最终选定蠕变模型参数。上述步骤先从定量分析入手,再根据具体影响因素进行定性分析,这两步可能互相交叉、多次重复,直至最终确定参数值,这一方法是感性与理性、定量与定性的综合,称为参数综合辨识法。经过这种参数综合辨识法得到的模型参数用于岩土工程的流变数值计算分析中,才能保证计算成果的正确合理性,保证岩土工程施工设计的安全可靠性。

[1] 翟 越,赵均海.基于自适应混合遗传算法的岩石类材料动态参数反演[J].地球科学与环境学报,2008,30(3): 286-291.

[2] 陶 波,伍法权,郭改梅,等.西原模型对岩石流变特性的适应性及其参数确定[J].岩石力学与工程学报,2005,24(17): 3165-3171.

[3] 冒海军,杨春和,刘 江,等.板岩蠕变特性试验研究与模拟分析[J].岩石力学与工程学报,2006,25(6):1204-1209.

[4] 袁海平,曹 平,万 文,等.分级加卸载条件下软弱复杂矿岩蠕变规律研究[J].岩石力学与工程学报,2006,25(8): 1575-1581.

[5] 赵永辉,何之民,沈明荣.润扬大桥北锚碇岩石流变特性的试验研究[J].岩土力学,2003,24(4):583-586.

[6] 李云鹏,王芝银,丁秀丽.流变荷载试验曲线的模型识别及其应用[J].石油大学学报:自然科学版,2005,29(2):73-77.

[7] 丁志坤,吕爱钟.岩石黏弹性非定常蠕变方程的参数辨识[J].岩土力学,2004,25(增刊):37-40.

[8] 徐卫亚,杨圣奇,谢守益,等.绿片岩三轴流变力学特性的研究(Ⅱ):模型分析[J].岩土力学,2005,26(5):693-698.

[9] 孙 钧,汪炳铿.地下结构有限元法解析[M].上海:同济大学出版社,1988.

[10] 李青麒.软岩蠕变参数的曲线拟合计算方法[J].岩石力学与工程学报,1998,17(5):559-564.

[11] 方开泰,马长兴.正交与均匀试验设计[M].北京:科学出版社,2001.

[12] 陈宝林.最优化理论与算法[M].北京:清华大学出版社, 1989.

[13] 陈炳瑞.岩石工程长期稳定性智能反馈分析方法及应用研究[J].岩石力学与工程学报,2008,27(11):2376.

Study on Choice of Creep Model Parameters for Mica-quartzose Schist

CHEN Wen-ling1,2,3,ZHAO Fa-suo1,2,3

(1.School of Geological Engineering and Surveying,Chang'an University,Xi'an710054,Shaanxi,China;
2.Key L aboratory of Western Mineral Resource and Geological Engineering of Ministry of Education,
Chang'an University,Xi'an710054,Shaanxi,China;3.Open Research Key L aboratory of Geotechnical
Engineering of Ministry of L and and Resources,Chang'an University,Xi'an710054,Shaanxi,China)

A seven-component linear viscoelastic plastic creep model of mica-quartzose schist was built according to the characteristic of triaxial creep test curve.Creep compliance-time curve and strain-time curve were fitted by means of least squares method,and then the parameters of creep model were obtained.The impact factors of obtaining parameters of creep model and the rationality and availability of those parameters were discussed.The result showed that the parameters obtained by the fitting of two curves were diverse from each other because of rating load times,primary load stress value and load time;creep model of mica-quartzose schist was significantly nonlinear;the parameters obtained by the fitting of creep compliance-time curve were not introduced,and the pattern of the parameters obtained by the fitting of strain-time curve was not significant in different stress levels; comprehensive identification method was suggested to replace any one single method which was incompletely used to obtain the parameters of creep model,and it could guarantee the rationality of the result of creep numerical analysis and the safe reliability of construction design in geotechnical engineering.

linear;viscoelastic;plastic;creep model;parameter;comprehensive identification method

TU452;P642.3

A

1672-6561(2010)02-0200-05

2009-10-19

国家自然科学基金项目(40872185)

陈文玲(1974-),女,新疆阿勒泰人,讲师,工学博士,从事岩土工程教学与研究。E-mail:dcdgx22@chd.edu.cn