利用GHZ态和EPR态隐形传送四粒子团簇态

2010-09-13陈智鹏胡之惠俞俊玮

上海电机学院学报 2010年3期

关键词：传态局域隐形

陈智鹏, 李渊, 胡之惠, 杨宇, 俞俊玮

(上海电机学院电子信息学院,上海200240)

利用GHZ态和EPR态隐形传送四粒子团簇态

陈智鹏, 李渊, 胡之惠, 杨宇, 俞俊玮

(上海电机学院电子信息学院,上海200240)

提出了1个四粒子团簇态隐形传送的理论方案。该方案利用1个三粒子 Greenberger Horne Zeilinger(GHZ)态和2个 Einstein Podolsky Rosen(EPR)态作为量子信道,对Alice拥有的粒子进行3次Bell基测量和1次投影测量,使得Bob端的4个粒子建立起纠缠关系,根据测量结果再对这4个粒子做相应的局域酉变换,完全在Bob端恢复出Alice端的团簇态,最终实现任意四粒子团簇态的隐形传送。

GHZ态;EPR态;隐形传态;团簇态;酉变换

Abstract：We propose a theoretical scheme for teleportation of four-particle cluster state using a three-particle Greenberger Horne Zeilinger(GHZ)states and two Einstein Podolsky Rosen(EPR)states as a quantum channel.Alice processes the particles using 3 Bell-basis measurements and a projection measurement.The entangled relation of the 4 particles is established on the Bob side.According to the measurements resalts,Bob processes these 4 particles using corresponding local unitary transformation,and the cluster state on the Alice side is completely recovered on the Bob side.Finally,teleportation of arbitrary four-particle cluster state is achieved.

Key words:Greenberger Horn Zeilinger(GHZ)state;Einstein Podolsky Rosen(EPR)state;teleportation;cluster state;unitary transformation

1993年,Bennett等人[1]首次提出了利用经典信道和Einstein Podolsky Roson(EPR)信道传送未知单粒子量子态,由此诞生了量子隐形传态的概念,从而开创了量子信息领域的一个全新方向。

在此基础上,Yan[2]提出了任意二粒子纠缠态隐形传态的方法;对于任意三粒子纠缠态的隐形传送,Dur[3]指出,利用随机性局域操作和经典通信(Stochastic Local Operation and Classical Communication,SLOCC)的方法,可以将任意三粒子纠缠态的隐形传送转化为三粒子Greenber-ger Horne Zeiling(GHZ)态|ψGHZ〉和三粒子 W态|ψW〉的隐形传送,而这两种量子态的隐形传送已有许多现成的方法可以完成[4-8]。

式中,αi为系数,可取任意复数值。

这样二粒子和三粒子纠缠态的隐形传送在原则上已得以解决。之后自然就引出了四粒子纠缠态的隐形传送的问题,四粒子纠缠态也有 GHZ态和W态的形式:

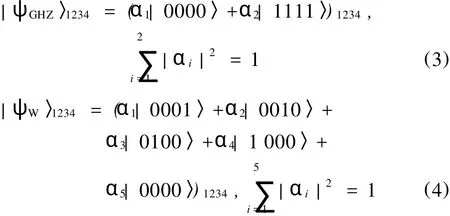
这两种状态的隐形传送可以仿照三粒子纠缠态的传送得以解决,但无论是四粒子纠缠态还是三粒子纠缠态都不具备一种状态——团簇态[9](Cluster States),这是 Raussendorf和 Briegel于2001年提出一种新的纠缠态:只有在粒子数 N>3时,才能显示出团簇态的性质。所以4个粒子是N粒子纠缠态要显示团簇态所需的最小数目,其一般形式为

本文利用1个三粒子 GHZ态和2个 EPR态作为量子信道,实现了四粒子团簇态的隐形传态。

1 Alice和Bob端的初始粒子状态

设 Alice端拥有粒子 1、2、3、4、5、8、10,Bob端拥有粒子 6、7、9、11,其中粒子 1、2、3、4 处于某一未知团簇态,则

式中,β,γ,χ均为系数,可取任意复数值。

Alice和Bob共享3个量子通道,其中一个是处于最大 GHZ态的粒子5、6、7,则

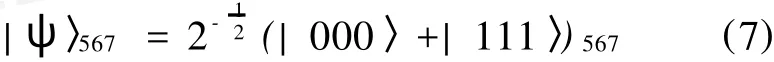
另2个都处于 EPR态,分别是粒子8、9和粒子10、11,

图1所示为Alice和Bob正常的粒子初始状态。

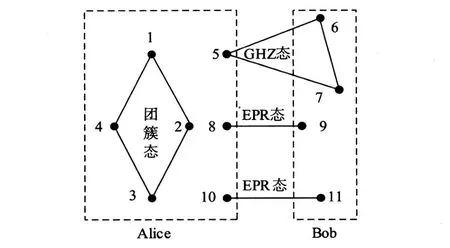
图1 Alice和Bob处的粒子初始状态Fig.1 Initial particle states on Alice side and Bob side

笔者的目的是将位于Alice端纠缠于粒子1、2、3、4上的未知团簇态,通过上述3个量子通道和经典信道传送到Bob端的粒子6、7、9、11上,从而完成隐形传态。该过程主要分为 2个步骤:①Alice端进行的Bell基测量和投影测量;②Bob端根据Alice告知测量结果,对粒子所做的相应局域酉变换。

2 Alice端的测量

根据量子力学的原理,可知粒子1～11构成的11粒子所处的量子态为

式中,⊗为张量积运算。

为了解除Alice端与Bob端间粒子的纠缠,建立Bob端粒子6、7、9、11的纠缠,从而实现四粒子团簇态的隐形传态,Alice端需要做如下测量:

(1)Bell基测量BM15。Alice对其拥有的粒子1、5做Bell基测量。该Bell基为

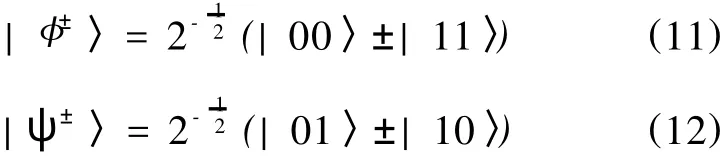
测量后,破坏了粒子 1、2、3、4的团簇态以及粒子5、6、7的 GHZ态,而建立起了 1、5之间的EPR态。测后状态如图2所示。

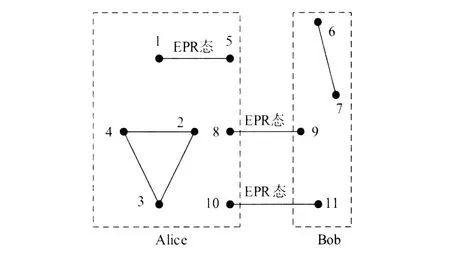
图2 Alice端进行 BM15后的粒子状态Fig.2 Particles states after BM15on Alice side

(2)BM28。Alice再对粒子2、8做Bell基测量。测后状态如图3所示。

(3)BM10,11。Alice再对粒子 10、11做Bell基测量。测后状态如图4所示。

(4)投影测量。Alice对粒子4做以|+〉、|-〉为基的投影测量,该基为

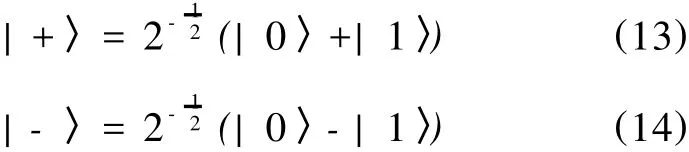
从而解除粒子4与粒子6、7、9、11的纠缠,使粒子6、7、9、11成为准团簇态(只要再做相应的局域酉变换则可称为团簇态)。测后状态如图5所示。

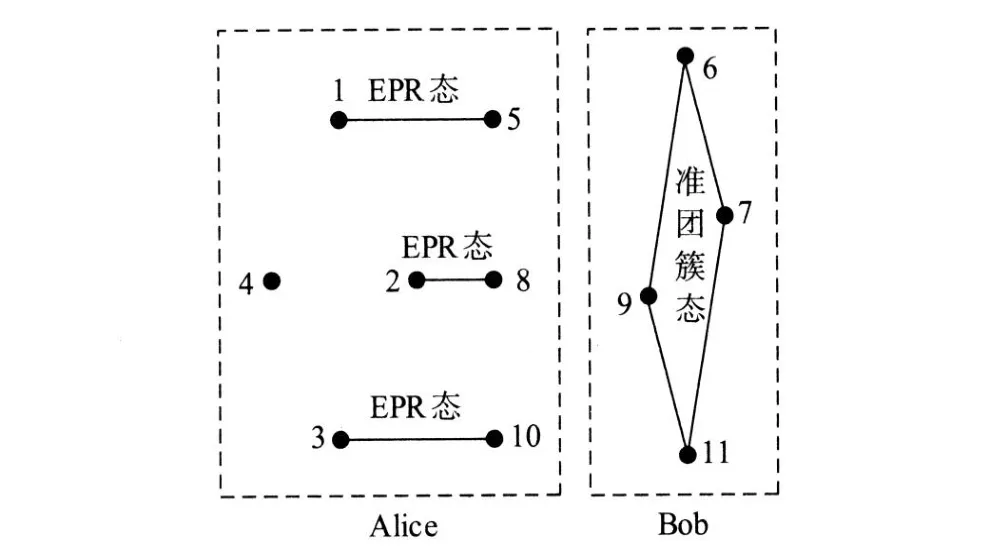
图5 Alice端进行投影测量后的粒子状态Fig.5 Particle states after projection measurement on Alice side

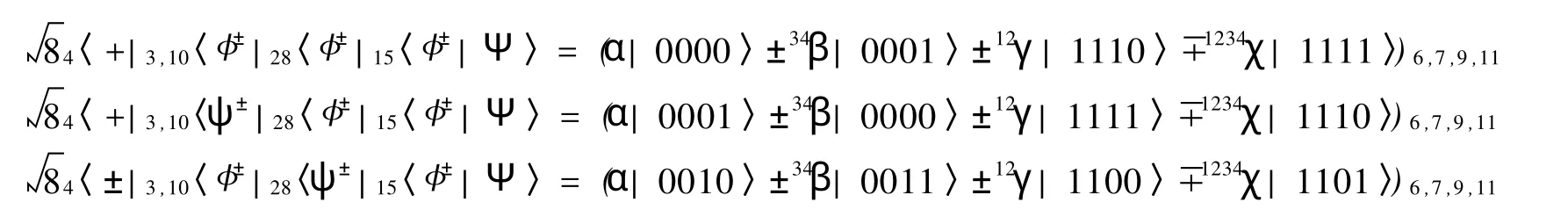
对应于Alice端测量的不同结果,Bob端的粒子 6、7、9、11 可能处于的状态为式中,±ij是根据粒子i,j所测得的状态来决定正负。如式中的±34的正负是由粒子3、4的测得状态|φ±〉3,10,|±〉4所决定。

根据粒子1、2、3、4测得状态的不同符号,可将所有结果列于表1中。

表1 Alice端测得状态与Bob端可能结果之间的符号关系Tab.1 Sign relationship between measured states on Alice side and possible results on Bob side

由表 1可见,虽然粒子 1、2、3、4测得状态的符号组合共有16种,但由于∓1234的符号完全由±34和±12决定 ,故最终结果中β,γ,χ的符号组合只有 4种:(+,+,-)、(+,-,+)、(-,+,-)和(-,-,+),Bob端的粒子 6、7、9、11 可能处于的状态共计8×4=32种。

3 Bob端的局域酉变换

Alice通过经典信道将BM15,BM28,BM10,11和投影测量得到的结果告知Bob端,Bob端根据不同的结果选择相应的局域酉变换算子,将粒子6、7、9、11 恢复为团簇态。

通过对Bob端粒子 6、7、9、11的可能结果进行观察发现,要恢复为Alice端的团簇态,必须对其中某些粒子进行比特翻转,另外还需调整正负号。故采用的酉矩阵为

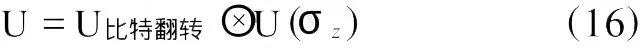
式中 ,σz为泡利矩阵

若Alice端得到的测量结果为〈φ|15,〈φ|28,〈φ|3,10,〈+|4,则粒子6、7、9、11的状态为

令酉矩阵 U比特翻转= (aij)16×16,其中

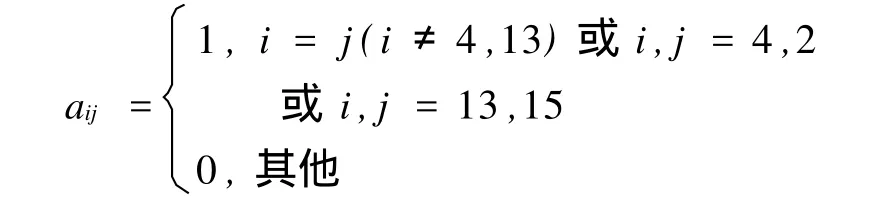
则 U比特翻转〈ψ|6,7,9,11=(α|0000〉+β|0011〉+

即为团簇态。由于结果中的正负号无需调整,则U(σz)=I,其中 I为单位矩阵。

根据Alice端测得的不同结果,Bob端所要进行的酉变换如表2和表3所示。变换后,Bob端可在粒子 6、7、9、11上完全恢复出 Alice端粒子1、2、3、4所具有的未知团簇态,从而实现团簇态的隐形传送。

表2 Bob根据表1调整正负号Tab.2 U(σz)used by Bob according to the Table1

表3 Bob根据Alice测得结果进行比特翻转Tab.3 Bit flip used by Bob according to the result on Alice side

4 结语

自Bennett等人提出隐形传态的概念后,该领域涌现出了大量的研究成果,对二粒子和三粒子的隐形传态研究得比较透彻,而四粒子的隐形传态尚未完全解决。基于此,本文提出了一种任意未知四粒子团簇态的隐形传送方案,为任意四粒子的隐形传态提供了一些便利。

该方案利用1个三粒子 GHZ态和 2个EPR态作为量子信道,对 Alice拥有的粒子进行3次Bell基测量和一次投影测量,解除三粒子 GHZ纠缠和2个二粒子EPR纠缠,而在Bob端的4个粒子间建立起准团簇态纠缠关系,Bob根据Alice的测量结果再对这4个粒子做相应的局域酉变换,完全恢复出Alice端的未知团簇态,最终实现任意四粒子团簇态的隐形传送。该方案的全过程都有严密的数学推导,从理论上论证了其正确性。

[1]Bennett C H,Brassard G,Crepeau C,et al.Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels[J].Physical Review Letters,1993,70(13):1895-1899.

[2]Li Yanfeng,Ge Tanhong,Yang Linguang.Probabilistic teleportation of two particle state of general formation[J]. Communications in Theoretical Physics,2002,37(6):649-654.

[3]Dur W.Vidal G,Cirac J I.Three qubits can be entangled in two inequivalent ways[J].Physical Review A,2000,62(6):062314.

[4]Chen Libing.Probabilistic teleportation of a three particle entangled Wtype state[J].Acta Photonica Sinica,2002,31:1308-1311.

[5]郑亦庄,戴玲玉,郭光灿.三粒子纠缠 W态的隐形传态[J].物理学报,2003,52(11):2678-2682.

[6]杨洪钦,谢树森,陆祖康,等.利用三粒子W态隐形传送三粒子 GHZ态[J].光学学报,2006,26(2):300-304.

[7]李艳玲,冯健.利用单个三粒子最大 GHZ态或两个EPR态隐形传送任意三粒子 GHZ态[J].物理学报,2007,56(4):1888-1894.

[8]张国华,王美玉,闫凤利.四粒子纠缠 W态的概率隐形传输[J].河北师范大学学报:自然科学版,2006,30(3):293-296.

[9]Briegel H J,Raussendorf R.Persistent entanglement in arrays of interacting particles[J].Physical Review Letters,2001,86(5):910-913.

Teleportation of Four Particle Cluster State Using GHZ State and EPR State

C H EN Zhipeng, L I Yuan, HU Zhihui, YAN GYu, YU J unwei
(School of Electronics and Information,Shanghai Dianji University,Shanghai 200240,China)

TN 911.2

1671-2730(2010)03-0135-05

2010-04-11