轴向磁通盘式永磁同步电动机噪声解析计算方法

2010-09-13李全峰赵朝会

上海电机学院学报 2010年3期

关键词：固有频率永磁定子

李全峰, 赵朝会, 谢源

(上海电机学院电气学院,上海200240)

轴向磁通盘式永磁同步电动机噪声解析计算方法

李全峰, 赵朝会, 谢源

(上海电机学院电气学院,上海200240)

用解析方法来计算轴向磁通盘式永磁同步电动机的噪声,使用MatLab编制计算程序,并将解析计算结果和实验结果进行分析比较。实验表明了利用解析法计算轴向磁通盘式永磁同步电动机噪声的可行性。最后,利用所编程序通过改变计算极弧因数来降低电动机噪声。

轴向磁通;永磁电动机;噪声

Abstract：This paper describes an analytical method to assess noise of axial flux disc permanent magnet synchronous motors(AFDPMSM).The program is developed with MATLAB.Computation results based on the analytical method are compared with measurements,showing feasibility of the method in predicting noise of AFDPMSM.The calculated pole arc factor is adjusted to achieve noise reduction by using the developed program.

Key words:axial flux;permanent magnet motor;noise

轴向磁通盘式永磁同步电动机(Axial Fluxdisc Permanent Magnet Synchronous Motor,AFDPMSM)因其较高的转矩密度和良好的动态响应特性[1-2],在各种驱动、伺服和控制领域得到了迅速推广和应用,但对其噪声与振动的研究却相对较少。由于电动机噪声是电机性能的重要参数之一[3-7],因此,对AFDPMSM噪声特性的研究很有必要[8]。本文针对结构较为简单的单盘式结构AFDPMSM(见图1)的噪声计算进行研究。

AFDPMSM噪声的计算一般有有限单元法和解析法2种。有限单元法有计算相对准确、直观等优点,但其对工程技术人员要求较高,量与量之间的关系不很明显,且计算相对复杂,耗时较长。相反,解析法则能较明显地反映出量与量之间的关系,计算相对简单,耗时较少。在电机设计初级阶段,利用解析法计算电机噪声能方便参量修改,则相对快捷。因此,研究解析方法计算AFDPMSM噪声有着十分重要的意义。

图1 单盘式结构AFDPMSMFig.1 Single disc structured AFDPMSM

1 AFDPMSM噪声的解析计算方法

当AFDPMSM运行时,气隙中存在基波磁场和一系列谐波磁场,这些磁场相互作用会产生切向力,其中,除产生使电机旋转的切向电磁转矩外,还产生随时间和空间变化的轴向力,这些轴向力作用在定子铁心和机座上,使定子发生形变,继而产生振动和噪声;且定子铁心静变形量 ds约与轴向电磁力波次数m的4次方成反比,与单位面积上的轴向力波幅值 Fa成正比,故幅值较大的低次数(m<5)轴向力波是引起AFDPMSM电磁噪声的主要根源,因此,在计算时,主要计算 m<5的轴向力波。

1.1 轴向电磁力的计算

1.1.1 基波磁场产生的轴向力基波磁场幅值即气隙磁密 Bδ,它所产生的轴向电磁力波 m=2p,其中,p为极对数;力波频率 f=2f1,其中,f1

为电源频率,则

式中,μ0为真空磁导率。

1.1.2 定转子谐波磁场相互作用产生的轴向力定子vb次谐波磁场与转子μa次谐波磁场相互作用产生的轴向电磁力波m=vb±μa,单位面积上作用的力波幅值为[9]

式中,Bvb为定子vb次谐波磁场幅值(T);Bμa为转子μa次谐波磁场幅值(T)。

将同次数、同频率的所有力波按相量合成叠加。设各个力波叠加后合成的幅值为 Fas,则在铁心单位长度下电机气隙圆周一个力极下作用的轴向电磁力平均值为[9]

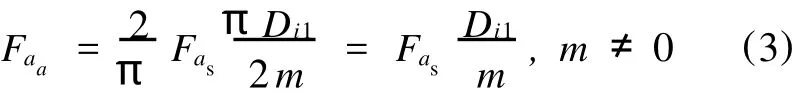
式中,Di1为定子铁心内径(m)。

当m=0时,轴向电磁力在整个气隙圆周均匀分布[8],故

1.2 轴向力引起的振动

当AFDPMSM运行时,气隙中交变的电磁力波作用于定子铁心,使它们随时间周期性地变形,即电机产生振动,此时,振动的频率就是轴向力波的频率。另一方面,电机有因其结构而决定的固有振动频率,为避免电机产生共振[10],故需计算电机定子的各阶固有频率 fn。

1.2.1 定子铁心静变形定子轭在轴向力 Faa的m次作用下的静变形为[9]

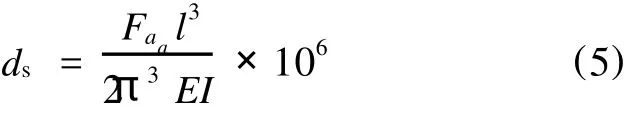
式(5)整理后得静变形

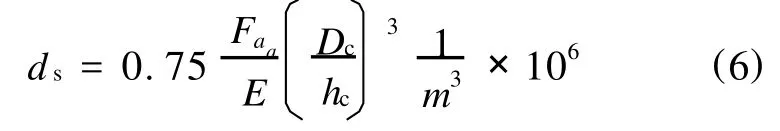
当m=0时,

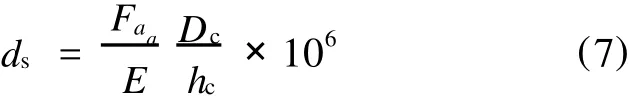
当 m=3、4,

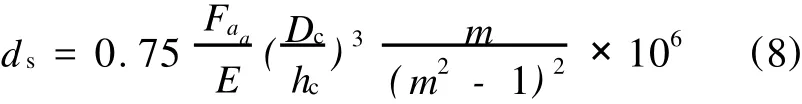
1.2.2 定子固有频率由于轴向结构电机与传统径向结构电机定子的结构不同,故应用于径向结构电机定子固有频率的计算方法对于AFDPMSM并不适用。因此,寻找AFDPMSM定子固有频率的解析计算方法是用解析法计算AFDPMSM噪声的关键。考虑到AFDPMSM定子的结构形状类似于扁的圆盘,故考虑可将AFDPMSM定子固有频率的计算转化为圆盘固有频率的计算问题[11]。因此,假设铁心质量均匀,则AFDPMSM定子固有频率为[12]

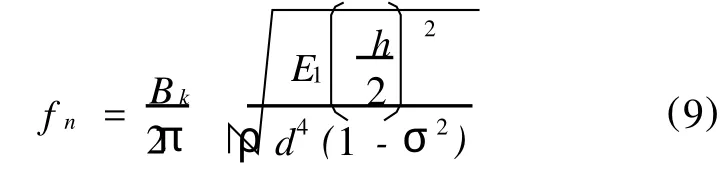
式中,h为定子的厚度;d为定子的外径;E1为定子材料的弹性模量;ρ为定子材料的密度;Bk为边界条件系数。

1.3 定子铁心振动幅值

当轴向力引起铁心振动频率 f即力波频率,其等于或接近 fn时会产生共振,此时铁心变形量将增大,实际变形量即定子铁心振动的位移幅值为[9]

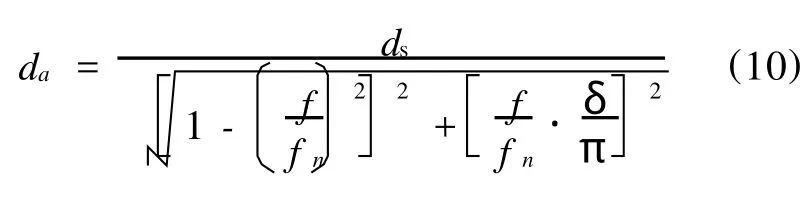
式中,δ为阻尼系数。

1.4 噪声辐射

由于AFDPMSM的结构尺寸远大于辐射波波长,故可近似地认为声波从无限大平面沿其法向辐射,即作平面辐射,故其声强级[9]

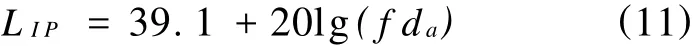
若在空气媒介时,式(11)的计算结果即为电机电磁噪声的声压级。将上述解析方法用Mat-Lab软件编程,其程序流程图如图2所示。

2 解析计算与实验对比

为验证该解析计算方法的正确性,分别对6.5 kW、20 kW、150 kW 3台AFDPMSM的噪声进行实验测量。实验所用的仪器为丹麦B&K公司生产的Pulse噪声与振动测试系统(见图3),在背景噪声为15.4 dB(A)的消声室内进行。此外,依据国家电机噪声与振动测试标准,根据电机轴中心高的不同,对3台电机分别采用不同的噪声测量方法:6.5 kW和20 kW电机采用半球面法测量,150 kW电机采用矩形包络法测量。利用解析方法编制的软件计算得到它们的噪声声功率级(A计权)与实验值声功率级对照如表1所示。

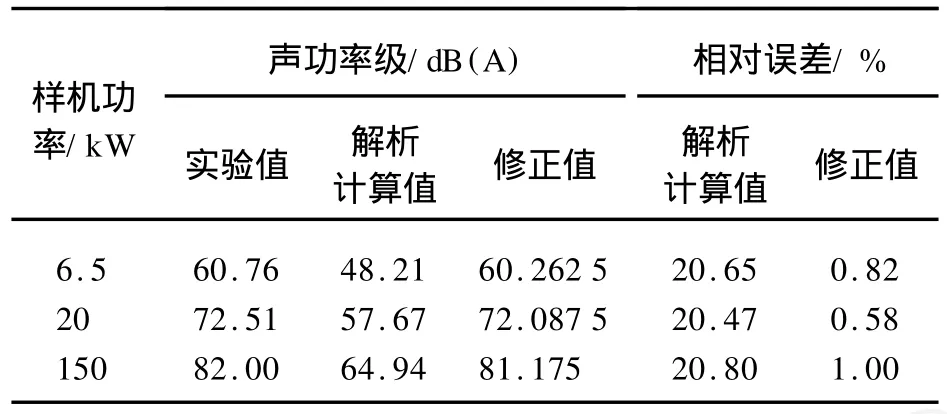
表1 解析计算值(修正前后)与实验值对比Tab.1 Comparison between analytically calculated(before and after modification)and experimental results

从表1可以看出,解析计算值比实验值要小,这主要与电机运行时产生的机械噪声和气载噪声有关,此外,电机本身的制造工艺对噪声值也有影响。考虑上述因素对AFDPMSM噪声的影响,表1中还列出了解析计算结果乘以修正系数1.25后得到修正后的计算结果。可以看出,修正后的3台样机相对误差较小,均不超过1%,能够满足工程上的要求。

3 计算极弧因数对噪声的影响

利用编制的AFDPMSM噪声解析计算程序,通过改变计算极弧因数来降低电机噪声。对于电机而言,极弧因数的选取是有一定原则的,过小,会降低电机的效率;过大,则会造成漏磁偏大。本文以20 kW样机为例,选取不同计算极弧因数以及对应的噪声值,如表2所示。由表可见,当计算极弧因数为0.845时电机噪声最低,为63.44 dB(A)。综合考虑,选取电机极弧因数为0.85,而此时电机噪声为63.453 dB(A)。

表2 不同极弧因数下的AFDPMSM噪声值Tab.2 Noise values of AFDPMSM under different pole arc factors

4 结论

本文针对AFDPMSM噪声的解析计算方法进行研究,在其定子固有频率的解析计算采用圆盘固有频率计算方法来完成;在声辐射计算中,根据AFDPMSM的具体结构特点,采用了平面辐射方法来计算其辐射的噪声值。通过3台样机的修正计算与实验值比较,证明了对于AFDPMSM在其电机设计的初步阶段可以采用该方法计算其噪声。最后利用该解析计算方法讨论了不同计算极弧因数对AFDPMSM噪声的影响,为设计低噪声AFDPMSM打下很好的基础。

[1]唐任远.现代永磁电机:理论与设计[M].北京:机械工业出版社,2000.

[2]周晖,袁从明,曹磊.电压不对称时永磁同步电动机的动态过程[J].南通大学学报:自然科学版,2007,6(3):68-71.

[3]Yang SJ.Low-noise electrical motors[M].Oxford:Clarendon Press;New Y ork:Oxford University Press,1981.

[4]Jang G H,Lieu D K.The effect of magnet geometry on electric motor vibration[J].IEEE Transactions on Magnetics,1991,27(6):5202-5204.

[5]Gieras J F,Wang C,Lai J C.Noise of polyphase electric motors[M].[S.l.]:Taylor&Francis Group,CRC Press,2006.

[6]舒波夫 ИГ.电机的噪声和振动[M].北京:机械工业出版社,1980.

[7]陈世坤.电机设计[M].2版.北京:机械工业出版社,2000.

[8]于慎波,王荔楠,周兆爽,等.盘式永磁电动机振动与噪声特性的研究[J].机械工程师,2007,(12):69-71.

[9]黄国治,傅丰礼.Y2系列三相异步电动机技术手册[M].北京:机械工业出版社,2004.

[10]吴建华.基于物理模型开关磁阻电动机定子模态和固有频率的研究[J].中国电机工程学报,2004,24(8):109-114.

[12]李全峰,王巍,宋志环,等.盘式永磁电机定子固有频率的研究[J].电气技术,2009(3):10-12.

Analytical Method for Calculating Noise of Axial Flux Disc Permanent Magnet Synchronous Motor