一类大集合容量伪随机序列集的线性复杂度研究

田金兵，邢 福弟，刘 古胜

（1.海南师范大学 初 等教育学院，海南 海 口 5 71158；2.荆楚理工学院 数 理学院，湖北 荆 门448200）

一类大集合容量伪随机序列集的线性复杂度研究

田金兵1，邢 福弟1，刘 古胜2

（1.海南师范大学 初 等教育学院，海南 海 口 5 71158；2.荆楚理工学院 数 理学院，湖北 荆 门448200）

具有大线性复杂度的序列可以抵抗Berlekamp-Massey算法攻击，提高数据的安全性，设计大线性复杂度伪随机序列是一个重要课题.使用d-齐次函数是增大序列的线性复杂度的一个有效方法.本文对正整数n=3m提出了一类周期为3n-1集合容量为3n的新序列集S（r），这里（r，3m-1）=1且1≤r＜3m-1.通过取适当的参数r，精确地计算出了它的线性复杂度.

序列；集合容量；线性复杂度

在密码学中，周期序列的线性复杂度指的是产生伪随机序列的最短线性反馈移位寄存器的长度，是衡量流密码系统强度的一项重要指标.在某些应用环境中的伪随机序列应具有较大的线性复杂度，这是因为线性复杂度小的序列是不安全的，密码分析者在知道这个序列少量元素的情况下可以用Berlekamp-Massey算法破译整个序列.因此，设计出具有较大线性复杂度伪随机序列一直是序列研究中的一个重要课题.

在文献[1]中，Klapper给出了一种增大d-齐次序列的线性复杂度的方法，人们证明了几类有较大的线性复杂度下界的d-齐次序列，如对小集合Kasami序列的各种推广［1-3］，这些序列有较大的线性复杂度，但它们的集合容量相对于序列长度依然较小.本文对于正整数n=3m给出了一类大集合容量的周期序列集 S（r），这里（r，3m-1） =1且 1 ≤r＜3m-1.通过取，精确计算出了它的线性复杂度为m·6w.证明了这类序列集有较大的线性复杂度.

1 基础知识

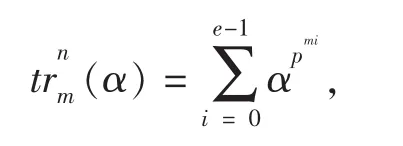
迹函数具有下列基本性质：

2 新序列集的构造

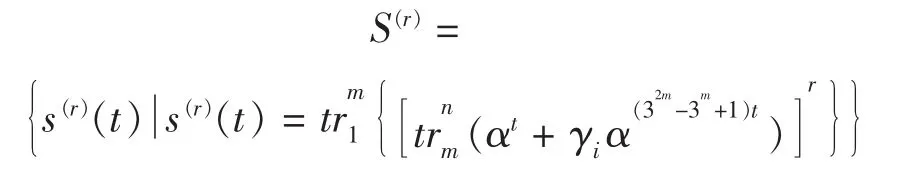
显然，如上所定义的序列集周期为3n，集合容量为3n-1，下面来研究它的线性复杂度.

Key在文献[4]中给出了计算序列的线性复杂度的方法：如果令 x = αt，此时二元序列 s（r）（t）可写成一个关于变量 s（r）（t）的多项式，那么二元序列s（r）（t）的线性复杂度 L S（s（r）（t））等于把 s（r）（t）展成关于变量x的多项式中次数不同的非零单项式的个数.Antweiler M.和Bömer L.把这个结论推广到p元序列中［5］.

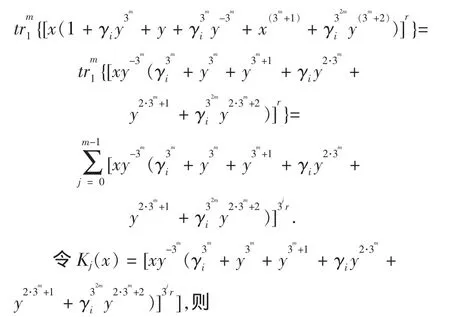
引理 1 当 j≠j′时，Kj（x）和Kj′（x）关于变量的展开式中非零单项式的次数互不相同.

证明 由于y=y3m-1，因此只需证明对于j≠j′总有 3jr≡3j′r（mod3m-1）.事实上，如果3jr ≡ 3j′r（mod3m-1），注意到 gcd（r，3m-1） =1，那么 3jr≡3j′r（mod3m-1），从而有 i=i′.

显然对于不同的j，Kj（x）关于变量x的展开式中非零单项式的个数相同.由引理1知，序列S（r）的线性复杂度 LS（S（r））等于 Kj（x）展开式中非零单项式的个数的m倍.令，则 Kj（x）展开式中非零单项式的个数和Φ（y）展开式中非零单项式的个数相同.这样就将计算序列S（r）的线性复杂度问题转化成计算Φ（y）展开式中非零单项式的个数问题.

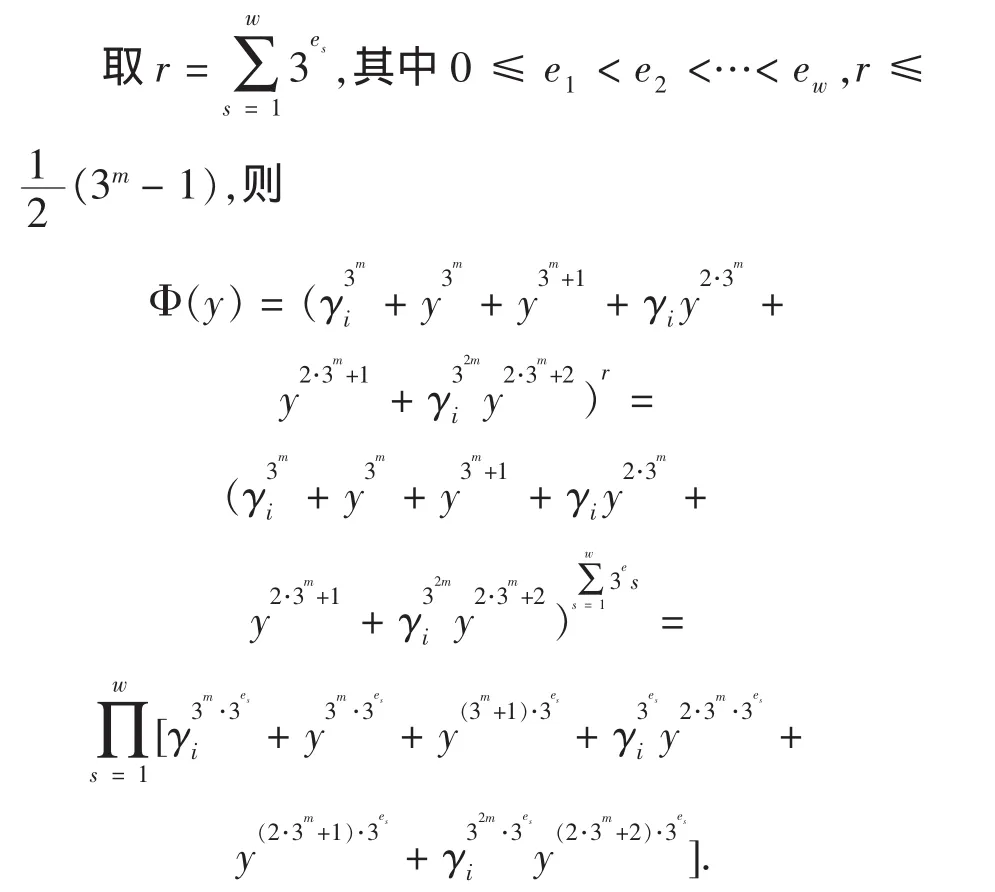
为了叙述的方便，定义集合的加法及数乘：

A⊕B={a+b|a∈A，b∈B}，μA={μA|a∈A}，μ为常数.

同时记 c·3m+d= （c，d），定义其加法及数乘：

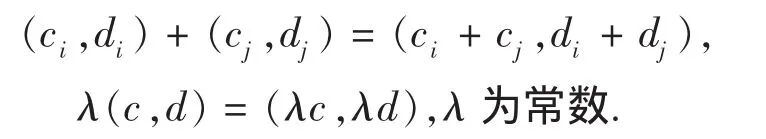
并规定（ci，di） = （cj，dj）当且仅当 ci=cj，di=dj.

显然Φ（y）展开式中关于y的指数构成的集合为

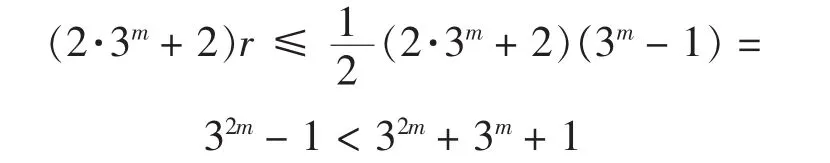
那么Φ（y）中关于的最大指数小于33m-1，因此Φ（y）展开式中关于y的非零单项式的个数就等于集合E种元素的个数.

引理2 集合E共有6w个元素.

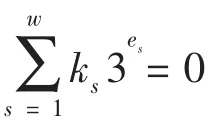
由上面的讨论立即得到：

3 结论

从上面的分析可知，本文给出的序列集不仅具有大的集合容量，而且具有较大的线性复杂度，特别地，当γi=1时，No证明了它是一条具有理想自相关的序列.这类序列适用于对线性复杂度要求较高的应用环境中.

表1 序列集S（r）与其它序列集的比较Fig.1 Comparison of the sequence S（r）with other sequences

［1］Klapper A M.D-form sequences:families of sequences with low correlation valuesand large linear spans[J].IEEE TransInform Theory,1995,41(2):423-431.

［2］No J S,Kumar P V.A new family of binary pseudorandom sequenceshaving optimal periodic correlation propertiesand large linear span[J].IEEE TransInform Theory,1989,35(2):371-379.

［3］Zeng X Y,HU L,LIU Q C.A family of binary sequences with optimal correlation property and large linear span[C].Proceedings of the 2006 IEEE International Conference on Communications.Istanbul,Turkey,2006.

［4］Key E L.An analysis of the structure and complexity of nonlinear binary sequence generators[J].IEEE Trans Inform Theory,1976,22(6):732-736.

［5］Antweiler M L.Complex sequences over with two-level autocorrelation function and a large linear span[J].IEEE TransInform Theory,1992,38(1):120-130.

［6］Jang JW,Kim Y S,No JS,et al.New family of p-ary sequences with ideal autocorrelation and large linear span[J].IEEE TransInform Theory,2004,50:1839-1844.

［7］Kumar P V,Moreno O.Prime-phase sequenceswith periodic correcation propertiesbetter than binary sequences[J].IEEE TransInform Theory,1991,37:603-616.

［8］Liu S C,Komo J F.Nonbinary Kasami sequences over GF(p)[J].IEEE TransInform Theory,1992,38:1409-1412.

责任编辑：毕和平

Study on Linear Span of a Pseudorandom Sequences Family with Large Family Size

TIAN Jinbing1， XING Fudi1， LIU Gusheng2
（1.College of Elementary Education，Hainan Normal University，Haikou 571158，China；2.School of Mathematics and Physics，Jingchu University of Technology，Jingmen 448200，China）

Application of sequences with large linear span can efficiently resist Berlekamp-Massey attack and improve security of data.The design of sequences with large linear span was an important research problem.A useful approach to construct sequences with large linear span was based on d-form function.For a positive integer n=3m,a sequences family S（r）with optimal correlation was proposed，where （r，3m-1） =1 and 1 ≤ r ＜ 3m-1.By taking suitable values of the parameter r,its linear span by in this paper was calculated accurately.

sequences；family size;linear span

TN 918.1

A

1674-4942（2010）03-0256-03

2010-04-30

海南师范大学青年教师资助项目（QN0802）；海南省自然科学基金资助项目（808152）