基于割线法计算单圆弧齿轮传动公法线长度

罗文翠 朱玉红 易湘斌

（兰州工业高等专科学校机械工程系，甘肃兰州 730050）

基于割线法计算单圆弧齿轮传动公法线长度

罗文翠 朱玉红 易湘斌

（兰州工业高等专科学校机械工程系，甘肃兰州 730050）

在圆弧齿轮传动及其测量尺寸公法线长度的计算原理基础上，以67型单圆弧齿轮为例，提出了利用割线法计算单圆弧齿轮公法线长度的原理、求解方程流程图、迭代方程及编程，比手工计算大大降低了工作量，而且精度也得到了很好的保证。

单圆弧齿轮 公法线 割线法 应用

圆弧齿轮传动是近几年发展起来的一种新型齿轮传动，单圆弧齿轮传动的小齿轮采用凸齿，大齿轮采用凹齿。自上世纪60年代以来，有关工厂、学校和科研单位进行了大量的研究、试验和推广工作，取得了较大成绩。和渐开线齿轮传动相比较，单圆弧齿轮传动具有一系列优点：①当量曲率半径大，齿面接触强度高;②摩擦损失小，传动效率高，齿面磨损小;③齿面磨损均匀，易跑合，具有良好的跑合性能;④无根切现象，其最少齿数仅受轴的强度及刚度限制，Zmin=6～8;⑤振动噪声比渐开线齿轮小，制造工艺简单。

工程实践证明，在几何参数相同的条件下，单圆弧齿轮承载能力比渐开线齿轮高1～1.5倍。鉴于以上优点，单圆弧齿轮受到各国齿轮界的普遍重视，我国正在冶金、石油、矿山和起重运输机械等领域逐渐推广使用。

1 单圆弧齿轮传动测量尺寸——公法线长度的计算

经过多年对单圆弧齿轮传动的测量研究，目前已建立一套较为完善的理论体系，并且在实践中得到了良好的应用。但是随着单圆弧齿轮传动向高速、重载、大功率方向的发展，对测量技术提出了更高的要求，因此需要不断完善现有的测量方法、计算方法，提高测量技术，加强对新测试方法的研究。

单圆弧齿轮传动测量尺寸的计算方法和渐开线齿轮基本相同，但是与基准齿形有关的检验项目，如弦齿深、齿根圆直径、齿厚、公法线长度等尺寸都比较复杂。

1.1 单圆弧齿轮公法线长度的计算原理

单圆弧齿轮公法线长度的测量，是一个基本的检测项目，目的是控制齿形厚度。其计算方法是计算两个有规律变化曲面之间的公法线长度。从数学角度讲，它的实质是求二元函数的极值，但对于单圆弧齿轮来说，基于齿面是法向圆弧螺旋面的特性，齿面上任一点的法线位于过该点并与准线相垂直的平面内且和该平面内圆弧曲线的法线重合。这样问题就简化很多，此二异侧齿面的公法线势必与该二侧面的两准线相交并垂直，于是单圆弧齿轮公法线长度的计算归结为计算两条螺旋线（准线）之间的最短距离。基于以上原理可求出双圆弧齿轮的公法线长度和跨测齿数，计算公式如表1。表中公式说明如下：

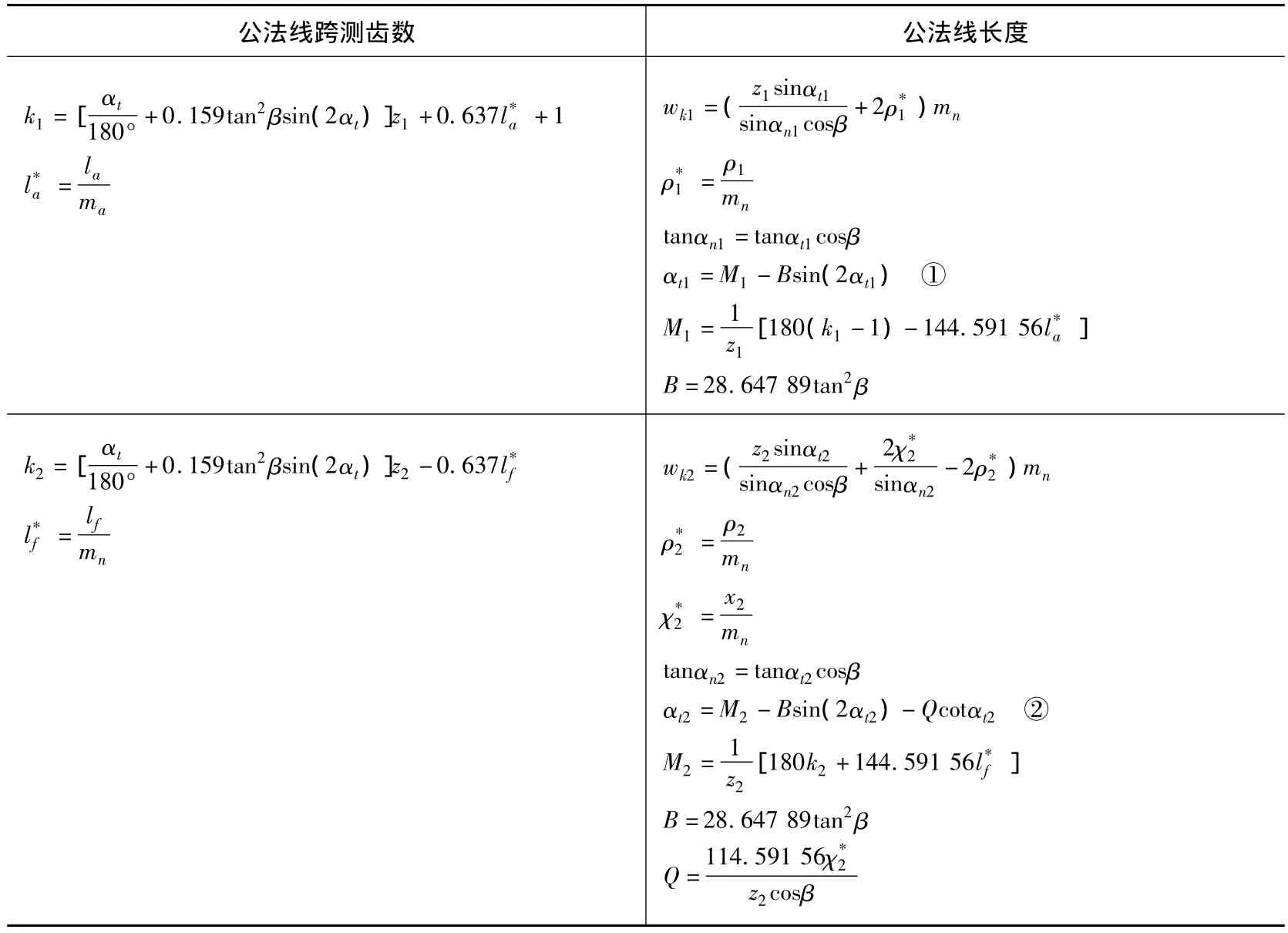
表1 测量尺寸计算公式

（1）对于跨测齿数 k1、k2的计算，其公式中 z1、z2分别为大小齿轮齿数，mn为法面模数，αt为理论接触点处端面压力角（tanαt=tanαn/cosβ），αn为法面压力角，β为螺旋角，lα为凸齿齿廓圆心偏移量，lf为凹齿齿廓圆心偏移量，ρ1为凸齿齿廓圆弧半径，ρ2为凹齿齿廓圆弧半径，x2为凹齿齿廓圆心移距量。式中上标为*的尺寸参数是指该尺寸与法面模数mn的比值，根据齿轮法面模数查手册可得。由于以上参数均为已知或可求，故k1、k2可方便求出，计算结果须向上圆整。

（2）公法线长度 wk公式中 αt1、αn1、αt2、αn2分别为小齿轮和大齿轮在测量时触头与齿面接触处的端面压力角及法面压力角，对于wk1、wk2公法线长度的计算，关键在于①、②两超越方程的求解。传统计算采用手工完成。计算时初取αt1=αt2=αt，进行第一遍计算，重复多次，直到αt1、αt2的误差在1″内为止。但此种计算方法较繁琐，应用困难。以下给出采用割线法求解两超越方程进行公法线长度计算的编程计算方法。

1.2 割线法原理简介

割线法是一种重要的逐次逼近的求解法，它是采用某个固定的公式把所选定方程根的初值代入，以校正根的近似值，使之逐渐精确化，最后得到满足要求的解。割线法是一种常用的迭代方法，其基本方法是把非线性方程转化为某个线性方程来求解。

如图1所示，割线法是以过曲线上两点（xn－1，f（xn－1））、（xn，f（xn））的直线为

设已知方程f（x）=0的一个近似根为x0，则函数f（x）在x0附近可用一阶泰勒多项式f（x）=f（x0）+f′（x0）（x－x0）来近似表示。因此方程f（x）=0在点x=x0可近似地表示为 f（x0）+f′（x0）（x －x0）=0，设 f′（x0）≠0，则线性方程的解为 x=x0－f（x0）/f′（x0）=x1。

重复以上过程得到迭代公式为xn+1=xn－f（xn）/f′（xn）。再用差商［f（xn）－ f（xn－1）］/（xn－ xn－1）代替导数 f′（xn），得迭代公式

按此公式计算方程的近似解称为割线法。

用割线法求非线性方程的解，必须给出两个初始值x0与x1，通常取根所在区间的端点即可。一般，用割线法求所求前后两次迭代误差不超过允许的误差，即以｜xn－xn+1｜＜ε为停步准则，即 ：可取xn为方程的根，误差不会超过ε。

1.3 利用割线法求解方程的流程图

利用割线法求解方程，其流程图如图2所示。

1.4 迭代方程

整理①、②两方程并对此求导，得到

得到具体迭代方法

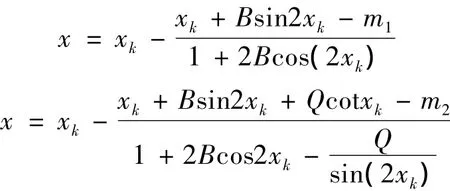
1.5 程序（略）

2 实际应用

基于以上程序，对某厂生产的一对67型单圆弧齿轮（表2）传动公法线长度进行计算。

表2 单圆弧齿轮基本参数

计算精度E取值为0.000 01，执行程序，计算结果如下。

3 结语

基于割线法进行单圆弧齿轮公法线长度计算方法，复杂的计算过程借助于计算机，比手工计算大大降低了工作量，而且精度也得到了很好保证，为生产提供了方便，此方法已在多家机械工厂推广。

1 王志，谢华锟，王贵成.锥齿轮测量原理以及测量仪器最新进展［J］.电测与仪表，2005（8）

2 谢华锟，王志，石照耀等.锥齿轮测量技术的最新进展［J］.工具技术，2003，37（10）

3 吕罕聪.螺旋锥齿轮测量方法研究［D］.中国优秀硕士学位论文全文数据库，2007（2）

4 丁丽娟.数值计算方法［M］.北京：北京理工大学出版社，1997：193～196

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Calculate the Common Normal Line’s Distance of Single Arc Gear Based on Secant Method

LUO Wencui，ZHU Yuhong，YI Xiangbin
（The Mechanical Engineering Department，Lanzhou Higher Polytechnical College.Lanzhou 730050，CHN）

We provided a way used secant methord and put forward the calculating principle of the common normal line，the flow chart，the alternating equation .This method was based on the calculating principle and formula of the double arc gear’s driving and measuring common normal Line’s distance and made 67 arc gear as an example.It creased labor power firmly and the precision was also increased.

Single Arc Gear;Normal Line;Secant Method;Application

罗文翠，女，1969年生，副教授，主要研究方向为结构设计、优化设计，已发表论文20余篇。

p

2009―07―29）

10332