最小二乘估计法在药品采购中的应用

卢佳聪 张 欣

最小二乘估计法在药品采购中的应用

卢佳聪 张 欣

目的 分析北京大学口腔医学院门诊药品销售现状及影响因素，预测未来门诊药品采购量。方法 对北京大学口腔医学院口腔黏膜科月挂号人次与Z药品的销售量数据进行统计分析，运用最小二乘估计法构建预测模型。结果 北京大学口腔医学院口腔黏膜科月挂号人次与Z药品的销售量保持着稳定的线性关系。结论 通过挂号人次对药品销售量进行预测，可以科学地确定门诊药品采购量，优化医院的资源的利用。

口腔病学；药品采购；预测；最小二乘估计法

北京大学口腔医学院是一所三级甲等口腔专科医院，日门诊量2600余人次，设有16个临床科室、10个医技科室，拥有牙科综合治疗台300余台，承担着来自北京及全国各地口腔及颌面部疾患患者的诊治工作，临床用药在口腔专科医院中具有一定代表性。

1 研究目的

由于病种越来越多，药品的供求关系及流通环节越来越复杂；由于某些特殊原因，药品用量出现突增或骤减的情况，加之沟通渠道的问题，药品采购人员无法及时做出应对措施，以满足患者用药的需求，使得在原有手工管理模式下，完全依赖于人的经验来预测药品的采购量是低效率的，而建立药品预测模型是非常必要的。

预测药品采购量目的在于促进药品供应由经验管理向科学管理转变，使定性管理逐步向定量管理转化，使药品采购量的预测比较准确，使被动的保障工作变为主动地、有计划地进行。通过药品销售预测确定采购量可以优化药品采购，解决药品库存占用大量资金的问题；同时，减少因药品管理带来的成本的消耗；加速资金周转，提高资金利用率；避免药品囤积，减少报废风险，降低损失；在降低药品库存的同时保证临床药品供应，同时还可以辅助解决临床用药无规律的问题[1]。

2 资料与方法

2.1 模型的建立

2.1.1 数据资料

由于医院药品种类繁多，首先，用ABC分析法确定重点品种。即统计出每月药品销售额，从大到小排序，计算所有药品总销售额，以达到总销售额的70%、20%、10%划分出ABC三类和各类品种数目。A类药品即为重点关注的品种。资料来源于北京大学口腔医学院门诊药房2008年12月至2010年6月药品管理软件的门诊药品销售数据，Z药品为稳定居于医院门诊销量第一的药品，由于Z药品只有口腔黏膜科的医师有处方权，所以数据选取的是，口腔黏膜科的月挂号人次和Z药品的销售量，见表1。

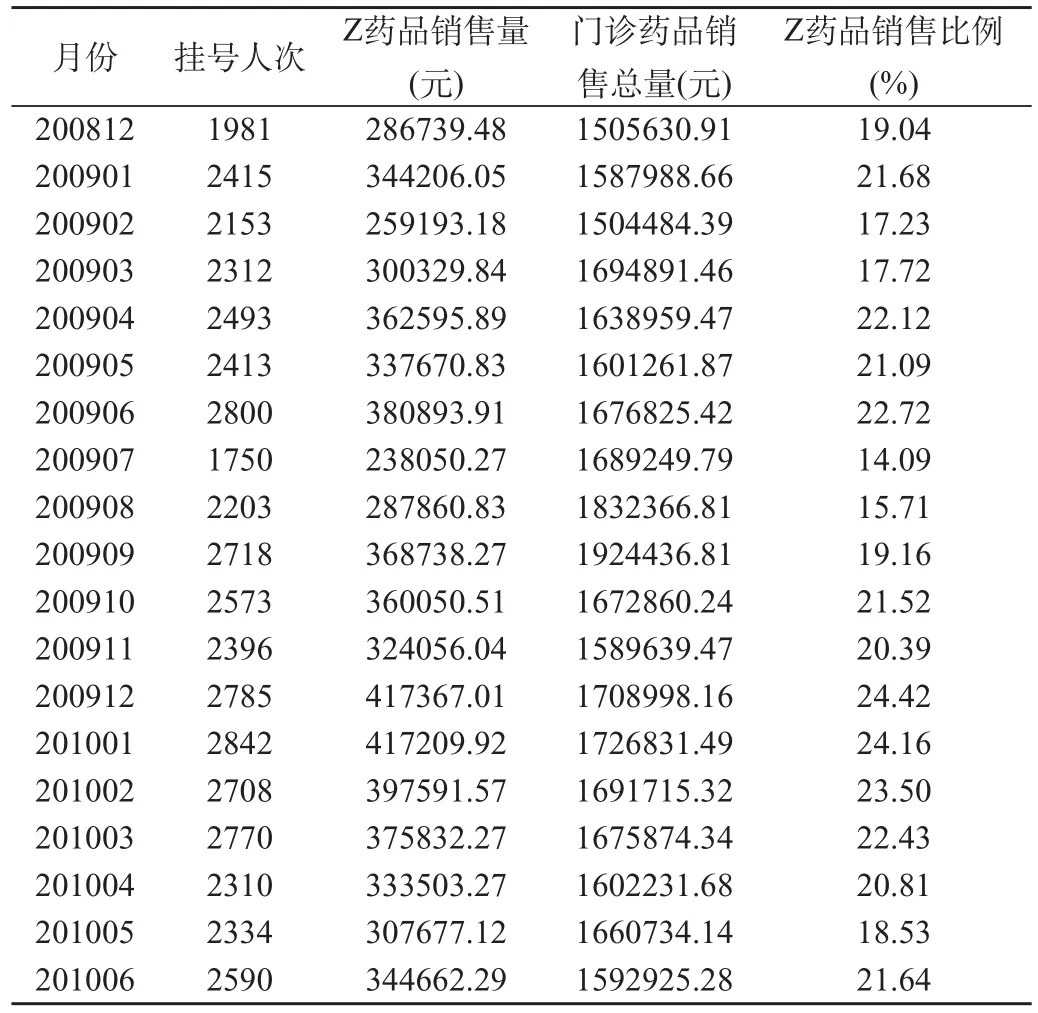
表1 2008年12月至2010年6月口腔黏膜科月挂号人次与Z药品的销售量

表1可见，Z药品销售量变化没有时间规律，变动幅度较大，完全依赖于人的经验无法准确预测药品的采购量，以满足患者的需求。

2.1.2 拟合2008年12月至2010年6月口腔黏膜科月挂号人次与Z药品的销售量散点图

由图1可见，口腔黏膜科月挂号人次与Z药品的销售量之间具有明显的线性关系。所以我们可以试图通过最小二乘估计法来对这两个变量进行拟合。

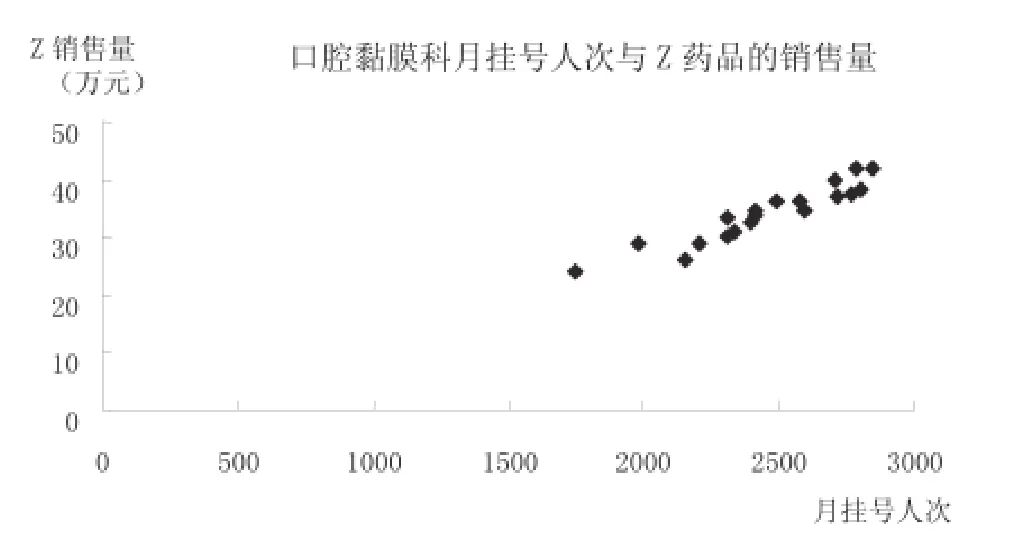
图1 2008年12月至2010年6月口腔黏膜科月挂号人次与Z药品的销售量散点图

2.2 运用最小二乘估计法对口腔黏膜科月挂号人次与Z药品的销售量进行拟合

构造统计关系的目的通常是为了预测或说明一个或多个可以控制或解释的变量的变化对另一个变量的影响。回归分析预测法，是在分析市场现象自变量和因变量之间相关关系的基础上，建立变量之间的回归方程，并将回归方程作为预测模型，根据自变量在预测期的数量变化来预测因变量。回归分析预测法是一种重要的需求预测方法，当我们在对需求未来发展状况和水平进行预测时，如果能将影响需求的主要因素找到，并且能够取得其数量资料，就可以采用回归分析预测法进行预测。它是一种具体的、行之有效的、实用价值很高的常用需求预测方法。回归分析预测法有多种类型。依据相关关系中自变量的个数不同分类，可分为一元回归分析预测法和多元回归分析预测法。

一元线性回归分析预测法，是根据自变量X和因变量Y的相关关系，建立X与Y的线性回归方程进行预测的方法。对图一中的散点，我们可以写出Y=a+bX的线性方程，其中左边的变量Y成为非独立变量，右边的变量X称为独立变量。因为要预测Y的变化，所以很自然的是要选择是垂直离差平方和最小的直线。即最小二乘估计法的准则可以写成如下公式：

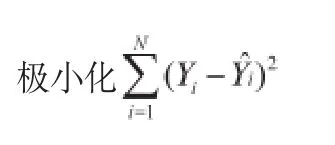
整理式3，式4得到方程组（称为正规方程组）

设Xi：黏膜科某月的挂号人次

Yi：黏膜科某月的患者购药量通过表1的数据，解得

a=-52114.74

b=159.72

y=-52114.74+159.72 x

2.3 模型的检验：拟合优度

回归残差是关于估计回归直线与数据之间拟合程度的一个很有用的度量，一个好的回归方程应该是有助于解释Y的大部分方差的方程。

总离差平方和的分解公式

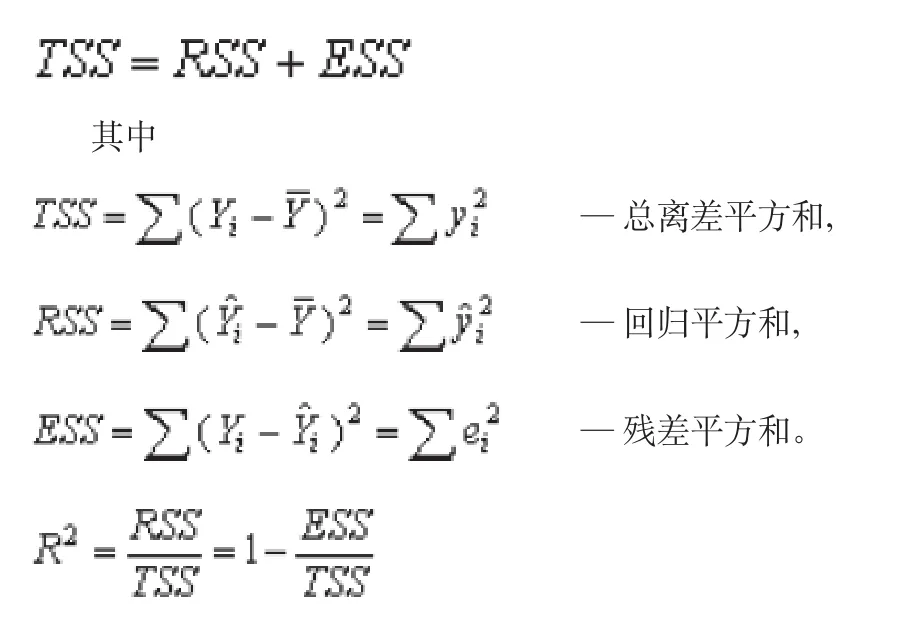
Yi为样本值，为样本均值，为预测值，∈[0,1]，值越高说明回归直线拟合的好，反之则说明拟合的不好

由样本数据解得，TSS= 52129850404.55,RSS=47118270581.06 ，

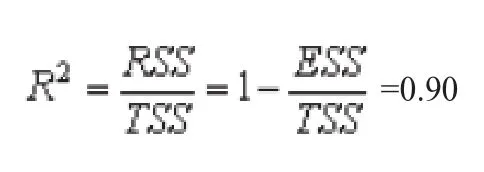
说明方程拟合的比较好。

3 利用回归模型进行预测

北京大学口腔医学院各科室通常于月底之前将计划好的下一个月的门诊挂号数量及具体安排通知挂号室，2010年7月口腔黏膜科的计划挂号量为2700个，将计划挂号量带入回归模型得到，7月份口腔黏膜科Z药品的预计用量为641937.66元。

4 讨 论

4.1 细化

除口腔黏膜病多以药物治疗为主外，其他大部分口腔疾病，如牙髓炎、冠周炎、根尖周炎，牙周炎和颌面部软组织外伤等均以医师的操作治疗为主，以药物治疗为辅，北京大学口腔医学院门诊用药大部分为口腔黏膜病用药，根据这种具体情况，进行门诊患者购药量预测时，就不能简单的利用挂号人次预测门诊患者购药量，应该根据各个科室和不同药品进行细化，分析影响各个药品使用的最关键因素，这样才能为药品采购提供更加精确的参考数据。同时，科室除了有一个月的挂号出诊计划，而且每一周都有具体的安排，并根据具体的情况进行调节，这样就可以缩小预测时间间隔，扩大样本空间，提供更加精确的预测[2]。

4.2 计算机系统的运用

由于医院的药品种类繁多，单凭手工计算是无法完成采购工作的，为了减少认为出错的概率，可以运用计算机采购系统，自动生成采购计划。同时，随着时间的推移，样本量的增大，预测模型可以得到进一步的优化，更加符合医院发展的需要[3]。

4.3 结合实际

在利用模型进行预测的时候，由于客观情况的制约，有些药品的销售不存在线性关系，不能光凭预测模型进行采购，为满足实际的需要，预防突发事件，要做好储备量，对特殊药品应进行提前采购和储备，要密切跟踪挂号人次的变化，及时跟相关部门沟通[4,5]。

[1] 王平根,吴海涛,高志平.医院药品预测模型[J].中国药学杂志,1999,34(3):200-201.

[2] 杨梅,高轶,杨洁.门诊量预测及变动趋势分析[J].中国卫生统计,2001,18(6):379.

[3] 郑利光,牛桂田.我院2005～2007年口腔门诊患者用药情况分析[J].中国药房,2009,20(20):2020-2022.

[4] 郭玉清,李文红,陈秀毅.医院药品采购和库存成本控制[J].中国医药指南,2009,7(2):25-26.

[5] Pindyck RS,Rubinfeld DL. Econometric Models and Economic Forecasts 计量经济模型与经济预测(4th Ed.)[M].北京:机械工业出版社,1999.

Least Square Estimation used for Drug Purchase

LU Jia-cong, ZHANG Xin
(Department of Finance, Peking University School of Stomatology, Beijing 100081, China)

Objective Get the status of the drugs sales amount for outpatients and the effect factors in Peking University School of Stomatology, forecast the volume of the drug purchase. Methods Analyses the data of registration of Oral mucositis and the drug Z sales amount from December 2008 to June 2010 in Peking University School of Stomatology, and use the statistics method of least square estimation to build the forecast model. Results There is steady linearity relationship between registration of Oral mucositis and the drug Z sales amount in Peking University School of Stomatology. Conclusion We can get the volume of drug purchase through the forecast of drug purchase for outpatients by the registration effectively that can optimize the resource of the hospital.

Stomatology; Drug purchase; Forecast; Least square estimation

R97

B

1671-8194（2010）24-0021-03

北京大学口腔医学院财务处（100081）