层次分析法在电子游戏教育性评价中的应用研究* <br/>---以内省型电子游戏为例

层次分析法在电子游戏教育性评价中的应用研究*
---以内省型电子游戏为例

2010-09-09□黄倩王蔚

中国远程教育 2010年19期

□黄倩王蔚

层次分析法在电子游戏教育性评价中的应用研究*
---以内省型电子游戏为例

□黄倩王蔚

电子游戏在教育中的应用得到了越来越广泛的关注,其中电子游戏的教育性评价问题是电子游戏应用于教育首先要解决的最重要的问题之一.本文针对目前存在的问题,将层次分析法引入到电子游戏的教育性评价中,提出了可操作的确定指标权重的流程图,以案例的形式展示了权重确定的过程,解决了以往凭经验确定权重导致的评估失衡问题.

层次分析法;电子游戏;评价体系;指标权重

前言

随着计算机网络和信息技术的进一步发展,电子游戏已经进入大众的娱乐生活.实际上电子游戏作为一种新型资源,完全可以为教育服务,并且电子游戏在促进青少年心理、智力、能力的健康发展方面有其独特优势.然而电子游戏评价体制严重阻碍了电子游戏为教育服务.近年来,国内外许多学者进行了电子游戏的教育性评价的研究[1-4].《电子游戏的教育性分类与评价》[1]一书从多元智能理论的视野将电子游戏分为八类,并提出了电子游戏的教育性的评价标准.由于目前对于电子游戏教育性评价的研究还处于初级阶段,指标权重的确定还没有一套科学的方法.因此本文以内省型电子游戏为例,提出了电子游戏教育性评价指标体系构建与权重确定的方法,以期为电子游戏评价指标权重的确定提供新的思路.

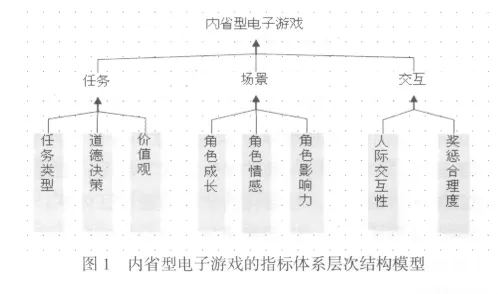
一、内省型电子游戏指标体系层次结构模型

内省型电子游戏是在《电子游戏的教育性分类与评价》一书中提出的,是指能够提高玩家内省智能的电子游戏.判断一款电子游戏是否属于内省型电子游戏,书中建立了一套评价指标体系,指标体系的建立既对电子游戏的组成元素进行了系统分析,又对电子游戏中的哪些要素能够促进内省智能的发展进行了考证.本文使用该书中所提出的指标体系,该体系分为两级指标,一级指标按照游戏的设计思路,把游戏的设计要素分为任务、场景与交互三大组成部分;二级指标以一级指标为主线,分别从中提取电子游戏对内省智能的培养因素,并经过严密的理论推导与实验验证进行指标筛选.内省型电子游戏的指标体系层次结构模型如图1所示.

二、层次分析法

1.权重确定方法

指标权重的分配反映了每一种指标的不同重要程度.有效分配指标的权重是运用指标体系进行公正评估的保证.有关综合评价中指标权重的确定方法,目前已有较多研究成果,根据确定途径,大致可分为两类:一类是基于决策者的经验和偏好,通过各指标属性进行比较而赋权的方法,称为主观赋权法,如专家调研法(Delphi法)、层次分析法(AHP法)[5]、环比评分法[6]等;另一类是基于相应属性指标的数据关系确定权重的方法,即客观赋权法,如主成分分析法[7]、因子分析法[8]、物元分析法[9]、模糊聚类法[10]、人工智能算法[11]等.

鉴于电子游戏的教育性评价指标中许多指标具有多层次性、难量化性等特征,不适合用完全定量的方式确定权重.而层次分析法(Analytic Hierarchy Process,AHP)是在定性方法基础上发展起来的定量地确定多因素权重的一种科学方法,它作为一种定量与定性相结合的方法,具有宏观性与主观性的特点,是将人们对定性因素的比较判断采用近似定量化的表示和处理方法,具有相当的灵活性[12],适合于对决策结果难于直接准确计量的场合[13].因此本文采用层次分析法来确定电子游戏的教育性评价指标权重.

2.层次分析法(AHP)原理

层次分析法是在定性方法基础上发展起来的定量确定多因素权重的一种科学方法,它是系统工程中的一种有效分析手段.该方法把复杂问题分解成各个组成因素,又将这些因素按支配关系分组形成递阶层次结构,将人的主观判断用数量形式表达和处理,在社会多个领域得到了广泛应用[14-16].

该方法的基本原理是:首先,通过分析复杂问题包含的因素及其相互联系,将问题分解为不同的要素并将这些要素归并为不同层次,从而形成多层次结构,在每一层次可按某一规定准则,对该层要素进行逐对比较建立判断矩阵;然后,通过计算判断矩阵的最大特征值和对应的正交化特征向量,得出该层要素对于该准则的权重,在此基础上计算出各层次要素对于总体目标的组合权重;最后得出不同方案的分值,完成对各方案的评价.

三、应用层次分析法确定内省型电子游戏的教育性评价指标权重

应用层次分析法确定指标权重一般分为5个步骤[14]:①建立层次结构模型(见图1);②构造判断矩阵;③层次单排序及其一致性检验;④层次总排序;⑤层次总排序的一致性检验.在实际应用中,层次总排序及层次总排序的一致性检验往往可以省略[13].因此本文提出了基于层次分析法的内省型电子游戏教育性评价指标权重确定方法的操作流程图,如图2所示.

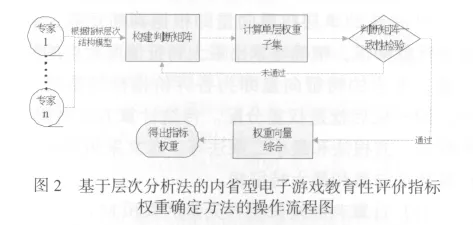
1.专家调查法,构造判断矩阵群

在层次分析结构中,对同一层次的各元素关于上一层次的重要性进行两两之间的判别比较,按两两指标比较结果构成的矩阵A=[aij],称为判断矩阵.矩阵中aij为下一层次指标中指标i对指标j的相对重要性.判断标准采用T.L.Saaty提出的1-9的标度法来指导专家构造判断矩阵(见表1).易见aij= {1/9,1/8,…1/2,1,2,…9},aii=1且aij=1/aji,即A是正互反矩阵.

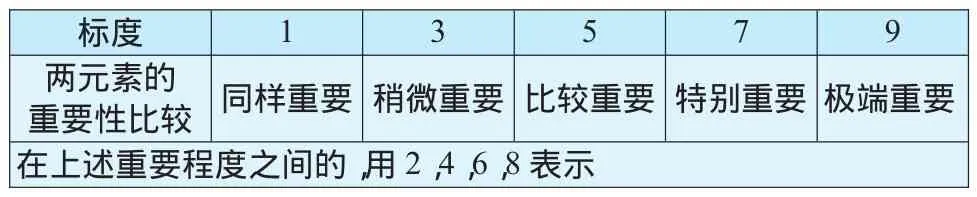
表1 T.L.Saaty的1～9标度法

为了更加准确地判断指标体系中的各个因素的重要程度,本文采用专家调查法建立判断矩阵,被调查的对象由8位电子游戏教育性分级分类的研究人员组成.下面列出了其中一位专家的判断矩阵群.

其中一级指标任务、交互与场景的判断矩阵为:

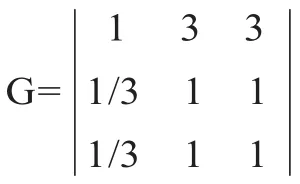
任务的二级指标:任务类型、道德决策、价值观的判断矩阵为:

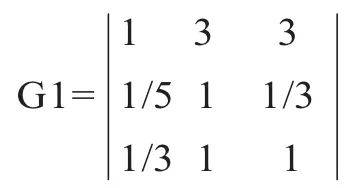
场景的二级指标:角色成长、角色情感、角色影响力的判断矩阵为:

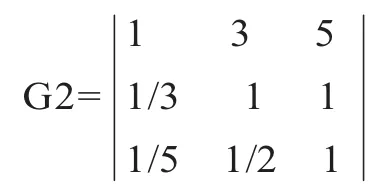
交互的二级指标:人际交互性与奖惩合理度的判据矩阵为:

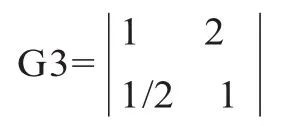
2.单层权重向量的计算

AHP法的单层权重向量即根据判断矩阵,利用线性代数知识,精确地求出最大特征值所对应的特征向量,所求的特征向量即为各评价指标的重要性排序,归一化后就是权重分配.传统计算方法有幂法、和积法、方根法和最小二乘法等.本文采用方根法来计算特征向量和最大特征根.

(1)计算判断矩阵每行元素的乘积Mi:

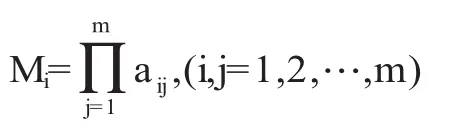
(2)计算Mi的m次方根:

(3)对向量W=(W1,W2,…,Wm)作归一化或正规化处理:

则W=(W1,W2,…,Wm)T即为所求特征向量.经计算上例中判断矩阵G、G1、G2、G3的权重向量分别为:

3.判断矩阵一致性检验

在评价指标体系复杂程度较高的情况下,有时两两比较可能会出现不一致的情况,如可能做出"甲比乙重要,乙比丙重要,而丙却比甲重要"的判断.因此需要对判断矩阵的一致性进行检验,检验使用公式:CR=CI/RI,其中CR为判断矩阵的随机一致性比率;CI=(λmax-m)/(m-1)为判断矩阵的一般一致性指标;为判断矩阵的最大特征根; m为判断矩阵的阶数;RI为判断矩阵的平均随机一致性比率,3-9阶的判断矩阵的RI值参见表2.

表2 矩阵阶数为3-9阶的RI值

4.综合求权重

经过上述步骤,根据每位专家的判断矩阵得到了8个权重向量集.权重向量综合法一般有判断矩阵综合法和权重向量综合法两种.每一种方法又包含加权几何平均法和加权算术平均法两种算法.本文采用权重向量综合法的加权几何平均法求多人判断矩阵群的权重向量.

假设判断矩阵G1的权重向量为:W1=(Wl1,Wl2,…, Wln)T,l=1,2,…,m,计算各权重向量相应分量的加权几何平均:

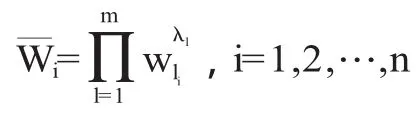
将之规范化:

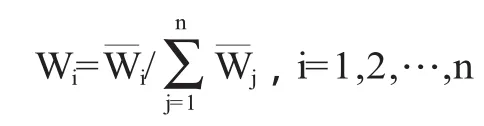
便得综合权重向量W=(W1,W2,…,Wn)T.

为了减轻计算量,本文采用层次分析法软件yaahp0.5.0的群决策功能,用权重向量综合加权几何平均法计算了专家的综合权重,得出了内省型电子游戏的教育性评价指标权重(见表3),并附上《电子游戏的教育性分类和评价体系》中凭专家个人经验确定的指标权重作为对比.

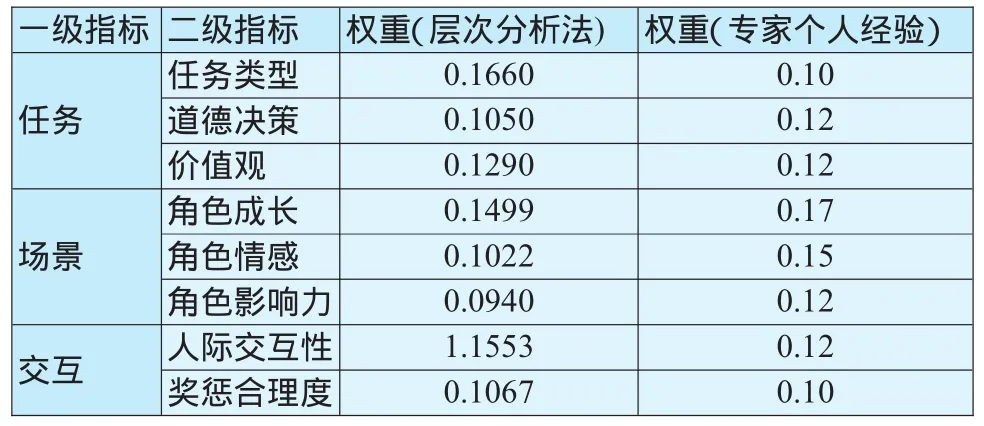
表3 层次分析法确定的指标权重与专家个人经验权重对比

四、结论

从表3的数据可以看出,通过层次分析法确定的指标权重,其中任务类型、人际交互性、角色成长在整个指标中所占的权重最大,这说明专家普遍认为这三项指标对于电子游戏能否提升玩家的内省智能起着非常重要的作用.

1.任务类型

2.人际交互性

根据多元智能理论,有效培养内省智能,需要有一个良好的人际关系环境,需要创设条件来关注人的内在心理活动和外在情绪表现.在一个良好的人际环境中才能形成正确的自我意识、自尊、自爱、自信等内省智能必不可少的要素.因此人际交互性对于内省智能非常重要.这在通过层次分析法设置的权重上也体现了出来.

3.角色成长

游戏中的角色成长是玩家直接参与的结果.角色成长经历越丰富,角色成长过程越复杂,越需要玩家去体验去分析角色所处的环境、能力大小等自身条件,然后做出决策,并对所做的决策负责.在游戏的过程中玩家对自身扮演角色的体验与分析评价实际上也就是自我体验、自我分析与自我评价,这正是内省智能的重要内容.因此其权重设置较高也是与实际相符合的.

通过表3的对比可以发现,依据个人专家经验确定的指标权重整体区分度不大,核心的、重要的指标在权重上没有得到充分的体现.而运用层次分析法确定的内省型电子游戏的教育性评价指标权重,较好实现了定性与定量的结合,提高了评价结果的合理性,比完全凭个人经验和知识来主观确定权重更科学、更合理,并且减少了主观因素的干扰.而且通过层次分析法软件可将复杂的矩阵计算轻易地实现,提高了指标权重的确定效率,从而为电子游戏的教育性评价指标权重的确定找到了一条可行的途径.

[1]王蔚.电子游戏的教育性分类和评价体系[M].北京:科学出版社,2010.

[2]卞云波,李艺.国内外电子游戏教育应用的理论研究综述[J].开放教育研究,2009,(1):93-97.

[3]张玲慧,王蔚.电子游戏在青少年教育中的应用现状及存在的问题[J].软件导刊(教育技术),2008,(10):31-34.

[4]卞云波,李艺.国内外电子游戏教育应用的理论研究综述[J].开放教育研究,2009,(1):93-97.

[5]王国华,梁墚.决策理论与方法[M].合肥:中国科技大学出版社, 2006:10-14.

[6]周德群.系统工程概论[M].北京:科学出版社,2007:24-28.

[7]罗志忠,张丰焰.主成分分析法在公路网节点要度指标权重分析中的应用[J].交通运输系统工程与信息,2005,(6):78-81.

[8]何晓群.多元统计分析[M].北京:中国人民大学出版社, 2004:8-15.

[9]聂艳,周勇,于婧等.基于GIS和模糊物元分析法的农用地定级评价研究[J].农业工程学报,2004,(5):291-300.

[10]许谦.确定模糊评价综合权重因素的一个方法[J].大学数学, 2005,(1):145-149.

[11]孙会君,王新华.应用人工神经网络确定评价指标的权重[J].山东科技大学学报(自然科学),2001,(3):84-86.

[12]中国系统工程学会决策科学专业委员会.决策科学理论与方法[M].北京:海洋出版社,2001:34-59.