基于小波的SAR图像融合算法及性能评价
2010-09-08孔兵
孔兵
(巢湖学院,安徽巢湖238000)
基于小波的SAR图像融合算法及性能评价
孔兵
(巢湖学院,安徽巢湖238000)
介绍几种基于小波变换的SAR图像的融合算法,利用多分辨小波变换的系数,采用低频图像的小波系数最大值作为融合后的低频系数,高频图像根据确定的融合规则,调整高频小波系数大小。并对融合图像质量进行了对比评价,得出了这几种融合方法的各自特点。实验结果表明,这几种方法能够在保留图像微小细节方面获得满意的结果。
小波变换;SAR图像;图像融合;客观评价
1 引言
近年来,信息融合理论和技术正成为信号和信息处理领域的研究热点,而图像融合在遥感、计算机视觉、医学、军事目标探测和识别等方面已得到广泛的应用,越来越成为信息融合的一个重要的研究方向[1]。
图像融合技术就是将来源于多通道的关于同一目标或场景的图像经过一定的处理,融合多个源图像中的冗余信息和互补信息,突出和强化图像中的有用信息,增加图像的可靠性以使综合后的信息更加丰富、对同一场景或目标的描述更为准确、更全面、更精细,图像的特征更适合观察,以利于对图像进一步分析、理解及目标的检测、识别或跟踪。因此,图像融合日益得到重视。
目前,图像融合处理主要在三个不同的层次上进行:像素级融合、特征级融合和决策级融合。像素级融合是特征级融合和决策级融合的基础,像素级融合主要采用简单图像融合方法,如极大值法、加权平均法等[2];基于塔形分解法,如高斯金字塔分解法、拉普拉斯金字塔分解法、对比度金字塔法等[3];以及基于小波分解法,如最大值选择策略、频带一致性策略、局部相关匹配策略、区域能量策略、边缘特征提取策略等[4-5]。但简单图像融合方法会对图像进行平滑,在一定程度上造成图像的边缘、轮廓变得模糊,融合能力最差。后二种分解法是一种多尺度、多分辨率图像融合方法,其融合过程是在不同尺度、不同空间分辨率、不同分解层上分别进行的,可以有针对性地突出各图像的重要特征和细节信息,从而得到更佳的融合效果。但相比之下,由于塔形分解是图像的冗余分解,各层数据有相关性,除梯度塔形分解有方向性外,其余均无方向性。
小波分析是时间-尺度分析和多分辨率分析的一种新方法,是时间与频率上的局部分析,能更加有效的提取信号和分析局部信息。可以将图像分解成一系列具有不同方向分辨率和频域性的子图像,由于分解中图像的数据量不变以及去除了相邻尺度上图像信息差的相关性,能够充分反映原始图像的局部变化特征。所以多分辨率小波变换在图像融合中得到广泛应用[6]。
对于同一地区SAR各波段图像特性差异较大,高波段SAR图像能提供场景外观景像,有点接近光学图像,而低波段SAR图像较黯淡,剩下的只是强反射景物和地表下的景物(含目标)的影像,因此各图像的相关性较之光学成像的各波段图像间的相关性更低,而不同的融合方法决定融合图像的质量好坏。本文利用小波变换对某机场不同波段SAR图像进行融合,并对小波融合几种算法的图像融合质量进行比较。
2 图像的小波变换与融合原理
小波变换是正交变换,这使得分解具有正交性,但正交小波变换的正交滤波器不具有线性相位特性,其产生的相位失真将会引起图像中边缘的失真,所以图像数据融合一般采用双正交小波变换[7]。
假定利用双正交小波变换将图像分解产生一系列小波系数{W1,W2,…Wn,Sn},其中n为分解层次,每一个Wi(i=1,2,…,n)对应一个特定分辨率尺度i,Sn是最大尺度下的低分辨率子带图像分解系数。其中Wi系数是分解尺度为i的高频子带图像分解系数,包括三个方向的高频子带图像分解系数分别为水平方向、垂直方向和斜线方向高频子带图像分解的系数。
若用H和G分别表示小波函数的镜像共轭滤波器的低通和高通滤波器组,S0表示原始图像,则二维的小波变换的快速分解公式为:

其中Hr,Gr和Hc表示镜像共轭滤波器H和G分别作用在行和列上。这样原图像S0的重构算法可以描述为:

图像的融合就是将多个经过预处理(包括去噪和配准)的图像分别进行相同层次小波变换分解获得小波分解系数{Wj1,Wj2,…Wjn,Sjn},其中j表示需要融合图像的数目,n表示小波分解的最大尺度。然后在不同的图像j对应的小波系数Wjk和Sjn中,根据一定的融合规则,选取最能代表图像特征和细节的小波系数组成新的小波系数序列,再根据小波逆变换重构得到融合后的图像。
3 基于小波变换的图像融合策略
图像的融合规则或方法是图像融合的核心,融合策略的优劣直接影响融合的质量和速度,融合策略就是决定哪幅图像的哪些小波系数对图像性能起相对决定性作用,从而保留这些信息。常用的融合策略有以下几种方法:
3.1 小波系数最大值融合策略
两幅待融合的图像经过小波分解后形成低频和高频小波系数阵,在对应低频系数方向上,采用加权平均或取较大值的方法来构成融合图像小波低频系数矩阵;在对应的高频系数方向上,采用选对应点最大值的方法来构成融合图像小波高频系数矩阵,最后经过小波逆变换可以得到融合后的图像。
3.2 频带方向一致性融合策略
两幅待融合的图像经过小波分解后,在对应低频系数方向上,采用取较大值的方法来构成融合图像小波低频系数矩阵。
在高频系数的选择采用频带方向最大值的方法:对于A图,在同一尺度的不同方向高频小波系数中求出相同位置上对应三点中的小波系数最大值max 1;对于B图,在同一尺度的不同方向高频小波系数中,求出同一位置上对应三点中的最大值max 2。如果两个最大值满足max 1>=max 2,则融合图像的对应尺度上不同方向高频系数对应点取A图相应三点,否则取B图相应三点作为融合图像小波高频系数矩阵,最后经过小波逆变换可以得到融合后的图像。
这种方法主要是小波分解后的三个高频具有一定的方向性,能代表各个方向上的细节部分信息,在同一尺度上,三个高频子带图像上对应同一位置处的小波系数,哪个方向上小波系数大,说明图像的细节部分主要集中在这个方向上,那么图像融合时就用该方向上的小波系数。
3.3 基于区域能量的融合策略
两幅待融合的图像经过小波分解后,在对应低频系数方向上,采用取较大值的方法来构成融合图像小波低频系数矩阵。
在某一尺度高频子带图像中选取一定大小的区域,分别计算待融合图像相应区域的能量EA,EB,同时计算两图像在该区域的匹配度MAB,并根据匹配度的大小来确定两待融合图像小波系数在融合图像小波系数中所占的比重,得到融合后图像高频小波系数阵实现图像融合。

如果

如果

则融合图像小波系数满足:

其中α是匹配度阈值,p为权重因子。
3.4 基于边缘检测算子融合策略
提出基于窗口的融合策略,考虑相邻像素之间的相关性,提取图像的边缘点,以图像的边缘为参考,围绕边缘建立融合策略。
对于融合的源图像分别进行小波分解,在对应低频系数方向上,采用取较大值的方法来构成融合图像小波低频系数矩阵。
对于反映图像细节的高频小波系数采用边缘检测来分析一定区域不同方向的边缘性,在同一尺度的同一区域的不同图像上采用边缘检测算子提取边缘特征。由于同一尺度的高频子图分别为水平方向、垂直方向、对角线方向三个方向的特征边缘,因此在不同的方向上采用不同的边缘敏感算子来提取边缘特征。水平方向特征提取算子采用对水平边缘敏感的sobel边缘提取算子Ph(i,j),同样,垂直方向特征提取算子采用对垂直边缘敏感的sobel算子Pv(i,j),对角线方向采用方向特征提取算子Pd(i,j),具体如下:

基于方向性的边缘提取算子,提取它们的边缘特征如下:


为了保持融合后的各个频带数据具有一致性,应采用概率方法对其进行一致性检测与调整。调整原理是采用“多数”原则,即在频带数据融合时对每个像素进行如下处理:如果某像素的8邻域中有多数像素较大特征值来自图像A,则该像素融合后的子带数据也调整为由图像A各方向的融合区域的系数确定,即取来自图A对应点的像素值,否则保持原数据不变。最后将获得的融合变换系数逐层进行离散小波的逆变换即可得到融合后的图像。
4 实验结果及性能评价
某处不同波段的SAR图像如图1所示;图2是采用小波系数极大值规则融合的图像;图3是采用频带一致性规则融合的图像;图4是采用能量准则融合的图像;图5是采用边缘算子特征提取规则融合的图像。

图1 不同波段原始SAR图像

图2 最大值规则融合图像

图3 频带一致性规则融合图像

图4 能量规则融合图像

图5 边缘特征提取融合图像
对于融合图像的客观评价是衡量图像融合效果的一个参考标准。由于SAR图像没有标准图像,客观评价主要是通过计算图像信息量指标来进行的。通常用均值、灰度标准差、熵值以及平均交叉熵和均方根交叉熵等统计特性对融合图像进行定量分析。
4.1 灰度均值

灰度均值为像素的灰度平均值,体现图像的平均亮度。
4.2 灰度标准差
设一幅图像的灰度分布为P={P(0),P(1),…,P(i),…P(L-1)},其中L为灰度级,P(i)为灰度等于i的像素数与图像的总像素数之比,且有成立。则图像的灰度标准差定义为:

灰度标准差反映灰度相对平均灰度的离散情况,标准差越大,则灰度分布越散,体现在视觉效果也越佳。
4.3 信息熵
图像的信息熵定义为:

信息熵从整体上表示了信息源的总体特性,熵越大图像中包含的信息量就越大,信息越丰富,融合效果会越好。
4.4 交叉熵
设两幅图像的灰度分布为:

则两幅图像的交叉熵定义为:

如果融合过程存在理想的融合图像F,由上式即可计算出融合图像R与理想图像F的交叉熵为CEN(R∶F)。如果不存在或无法构造出理想的融合图像,则上式分别计算出源图像与融合图像的交叉熵CEN(A∶F)和CEN(B∶F),再用下式计算出总体交叉熵:
平均交叉熵:

均方根交叉熵:

平均交叉熵和均方根交叉熵是评价两幅图像间差别的关键指标,它直接反映融合图像和原始图像的差异,差异越小,则该融合方法从该原始图像提取的信息量越多。因此,使用交叉熵可更准确地确定各种融合效果的优劣,交叉熵的值是反映融合效果的一个客观指标。
对比几种常用融合规则的定量分析结果如表1所示。
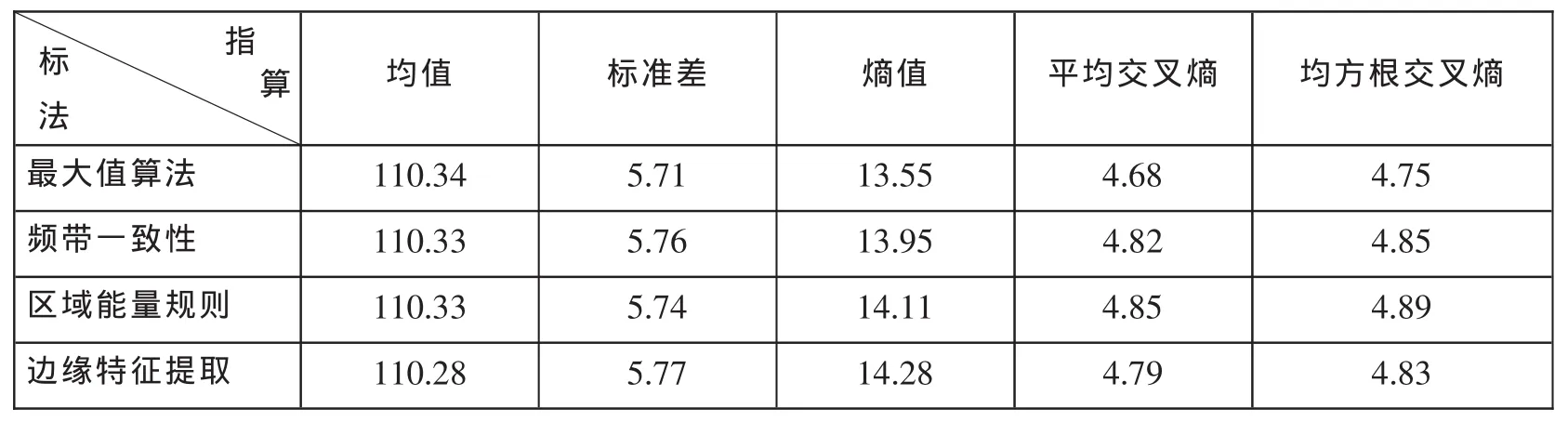
表1 文中几种融合算法的融合图像定量指标
从表1的数据可以看出,边缘特征提取方法融合结果的均值即平均亮度适中,标准差明显增大即其灰度分布最散,可见该方法最符合人眼的视觉特性。该结果熵值比其它方法都有较大幅度的提高,可见其细节更为清晰、信息量更为丰富。而交叉熵值较之其它方法则有明显降低,可见该方法从各原始图像提取的信息量更多。定量分析的结果表明,边缘特征提取方法较之其它几种方法性能明显有所改善。
5 结论
小波变换具有很好的方向选择性和空间-频率局域化特性。图像的小波分解是通过二维离散小波变换把图像分解为不同分辨率的高频和低频小波系数,分别提取二维图像的低频分量以及水平、垂直、45°方向的高频分量,图像融合就可以在这些特征域内进行针对性的融合。本文介绍了基于小波变换方法采用不同的融合策略对不同波段SAR图像实现融合,并将小波变换方法的几种融合策略的融合图像进行了分析比较。总体上说小波变换的多分辨图像分解融合效果应该说是比较好的,但边缘特征提取方法提出的融合算法考虑了不同方向的图像细节,使图像细节更真实更丰富,减小对源图像的预处理要求,使图像在整体上有较好的视觉效果。综合以上分析,在融合过程中,融合规则及融合算子的选择对于融合的质量起决定性作用,这也是图像融合研究的难点之一。
[1]Lemeshewsky G P.Multispectral Multisensor Image Fusion Using Wavelet Transforms[J].Pro.SPIE,1999,3716:214-222.
[2]AleaanderToet.MultiscaleConstrastEnhancementwithApplicationtoImageFusion[J].OpticalEngineering,1992,31:1027-1031.
[3]Toet A,et al.Merging Thermal and Visual Images by a Contrast Pyramid Optical[J].Engineering,1989,28(7):789-792.
[4]陆宏波,施惠昌.基于小波变换的图像融合方法[J].微电子与基础产品,2001,27(5):54-57.
[5]A Garzelli.Possibilities and Limitations of the Use of Wavelets in Image Fusion[C].IEEE,2002,66-68.
[6]Prasad L,Iyengar S S.Wavelet Analysis with Application to Image Processing[M].New York:CRC Press,1997.
[7]彭玉华.小波变换与工程应用[M].北京:科学出版社,2003.
Abstract:Image fusion algorithms of SAR image based on wavelet transform is introduced,the approach developed herein processes multi-resolution wavelet coefficients individually and adopt maximum of low-frequency image wavelet coefficients as the fusion low-frequency image wavelet coefficients,and uses high-frequency image fusion rules to adjust high-frequency image wavelet coefficients.Also this paper compared the quality of these fusion images,and obtains characters of these methods.Experimental results show that the proposed algorithms can retain subtle image detail and achieve an excellent effect.
Key words:wavelet transform;SAR image;image fusion;objective evaluation
责任编辑:澍斌
SAR IMAGE FUSION ALGORITHMS BASED ON WAVELET TRANSFORM AND PERFORMANCE EVALUATION
KONG Bing
(Chaohu College,Chaohu Anhui 238000)
TN919.8
A
1672-2868(2010)03-0067-06
2010-01-26
巢湖学院青年资助项目(项目编号:XLQ-200915)。
孔兵(1978-),男,安徽合肥人。硕士,讲师,研究方向:图像分析与信号处理。
