基于排序函数的区间数非线性规划模型及其解法
2010-09-08侯勇超赵开斌仇海全
侯勇超赵开斌仇海全
(1巢湖学院数学系,安徽巢湖238000)
(2安徽科技学院理学院,安徽凤阳233100)
基于排序函数的区间数非线性规划模型及其解法
侯勇超1赵开斌1仇海全2
(1巢湖学院数学系,安徽巢湖238000)
(2安徽科技学院理学院,安徽凤阳233100)
首先对区间数的排序方法进行了总结,给出了排序函数的定义,分类和性质,并利用排序函数对一些区间数的排序方法进行了讨论.其次,讨论了含有区间数系数的非线性规划模型,利用排序函数将其转化为一般的非线性规划问题。最后通过例子说明了方法的简便性和可行性。
区间数;排序函数;非线性规划
1 引言
不确定性越来越受到人们的关注,其中应用非常广泛的是随机性和模糊性。很多实际问题中,尤其是工程技术、管理决策等领域,由于测量的误差和主观因素的影响,往往只能得到一些数据的变化范围(区间数的形式)。从随机问题的角度来看,区间数可以视为服从均匀分布的随机变量,从模糊问题的角度来看,通过模糊集的分解定理和表现定理,可以利用区间数来研究模糊问题。Moore提出区间分析以来,很多学者对区间数的排序问题进行了研究。这些方法大致分为两类,其一是利用两个区间数比较的优势度,可能度或满意度,并通过判断矩阵构造排序向量进行排序,优点是尽可能多的保留了区间数的信息,缺点是无法对所有区间数进行排序,这类方法主要用于多属性决策;其二是将区间数的序通过映射转化为实数的序关系[1-3],优点是简单易行计算量小,缺点是转化过程中会丢失信息。对于区间数优化问题的研究主要集中在区间数线性规划[4-6],利用区间数的排序将其转化为普通的线性规划问题。对于区间数非线性规划,文献[7]讨论了含有决策风险因子的模型,并用遗传算法进行了求解。本文首先对区间数排序的方法进行了总结和归纳,提出了排序函数的概念并对已有排序方法进行了分类。然后,讨论了区间数非线性规划的一般模型,利用排序函数将其转化为一般的非线性规划模型。最后通过例子说明的方法的可行性和合理性。
2 区间数运算和排序方法
定义1[8]设R为实数域,称闭区间为区间数,分别称为区间数的左端点和右端点。R上区间数的全体记作I(R).
Moore(1979)提出如下区间数的排序方法:
定义4[9]设区间数当且仅当
这种方法无法比较区间数有重叠的情况。
Ishibuchi和Tanaka(1990)在研究区间数的线性规划问题时,提出如下两种区间数的序关系:
定义5[10]设区间数
以上均为区间数的偏序关系。
刘进生等提出了区间数比较的θ序:
定义7[1]设区间数
区间数的排序还可以借助于区间数的距离实现,首先定义区间数的距离,然后找出问题的极大或极小区间数作为参照,通过计算与参照区间数距离的大小进行排序。
Tran和Duckstein(2002)考虑了区间数每一点的差值,并进行积分得到:
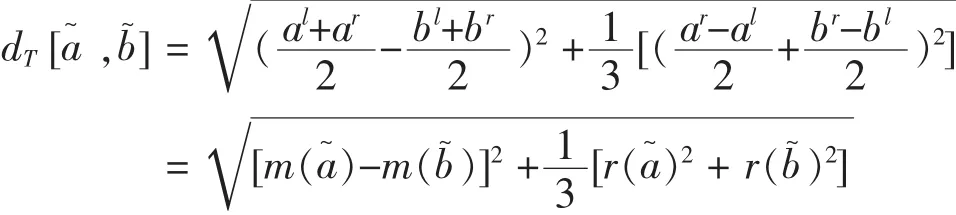
刘华文(2004)对上述距离不满足正定性进行了改进,定义区间数距离为:
定义10[2]设区间数,则两区间数的距离为
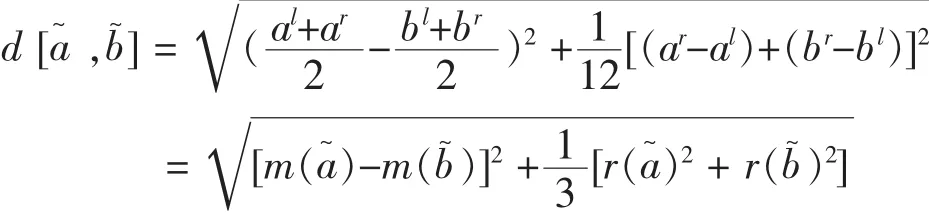
李霞等(2008)对以上距离某些情况下无法区分中点相同,半径不同的区间数的缺点进行了改进,得到:
定义11[3]设区间数,则两区间数的距离为

3 区间数排序函数及其分类
借助于区间数距离对区间数排序时,有几个缺点:第一,只能对极大区间数左侧或极小区间数右侧的区间数进行排序,无法对所有区间数排序;第二,具体实现时需要事先求出极大或极小区间数;第三,排序方式不灵活,决策者很难根据自己的需要来选择排序方式.事实上,可以用如下定义的排序函数来对全体区间数进行排序,决策者可根据自己的偏好,来选择恰当的排序方式.
定义12 若定义在平面区域D⊆R2上的二元函数z=f(x,y)满足如下条件:
(1)z=f(x,y)在定义域内连续;
(2)z=f(x,y)在定义域内分别关于x和y单调递增;
(3)z=f(x,y)在定义域内至少关于一个变量严格单调递增。
则称z=f(x,y)为区间数排序函数。
将x和y视为区间数的左右端点,则m和r是区间数的中点和半径。定义12的含义为区间数的一端点不变,另一端点变大时,区间数变大。定义13表明,区间数的中点相同时,用保守型排序函数排序,得到半径小的区间数较大的结果,而用风险型排序函数得到半径大的区间数较大的结果。这些都是与我们的直观认识相符的。
性质2保守型排序函数和风险型排序函数均可对中点相同的区间数辨别大小,结果相反。
性质3折中型排序函数均存在对于个别中点相同,半径不同的区间数无法辨别大小的情况。
证明:设z=f(x,y)=g(m,r)为折中型排序函数。由复合函数的连续性,z=g(m,r)为连续函数。由折中型排序函数的定义,∃m0,z=g(m0,r)关于r无严格单调性。则对m0,∃r1,r2(r1<r2)使得g(m0,r1)=g(m0,r2)。此时,由于区间数<m0,r1>和<m0,r2>对应的排序函数值相同,故z=f(x,y)=g(m,r)无法辨别它们的大小。
若z=f(x,y)存在偏导数,则有如下结论:
定理1设z=f(x,y)在平面区域D⊆R2上存在偏导数,若有则z=f(x,y)为排序函数。
定理2设z=f(x,y)为区间数排序函数,且有偏导数,则z=f(x,y)为保守型排序函数的充分条件为<0,z=f(x,y)为风险型排序函数的充分条件为
例1定义7中的排序方式可看作以z=f(x,y)=(1-θ)x+θy,(0≤θ≤1)为排序函数构造的区间数的序。其中=2θ-1,当时,z=f(x,y)为保守型排序函数;当时,z=f(x,y)为风险型排序函数;当为折中型排序函数,此时无法辨别中点相同半径不同的区间数。
用区间数距离定义的序关系可看作用相应的排序函数实现,以下用区间数[0,0]为参考点,对所有非负区间数(即左端点为非负实数的区间数)排序为例说明。
例2用定义8中距离排序相当于用以下排序函数排序
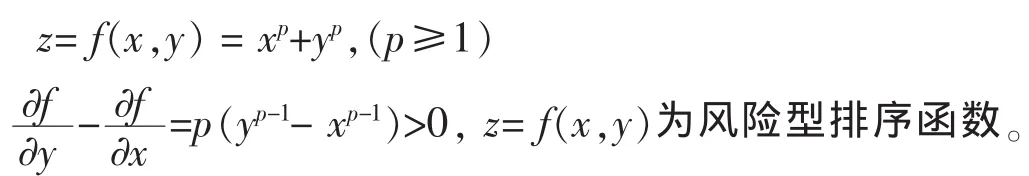
例3用定义9,10,11中距离排序相当于用以下排序函数排序

例4设f(x,y)=ax3+by3,(a>0,b>0),可得f(x,y)分别关于x,y单调递增,则f(x,y)为I(R)上的排序函数。并且,当a≤b时,f(x,y)为风险型排序函数;a>b时,f(x,y)为折中型排序函数。
例5设f(x,y)=ax·by,(a>1,b>1),可得,则f(x,y)为I(R)上的排序函数。并且a<b时,f(x,y)为风险型排序函数;a>b时,f(x,y)为保守型排序函数;a=b时,f(x,y)为折中型排序函数。
4 区间数非线性规划的模型
以上定义的排序函数可以用来求解如下区间数非线性规划模型[11]:

设z=f(x,y)为I(R)上的排序函数,则上述模型可转化为一般的非线性规划模型:

其中Zl(X),Zr(X)分别为目标函数左端点和右端点,S为问题的可行域。
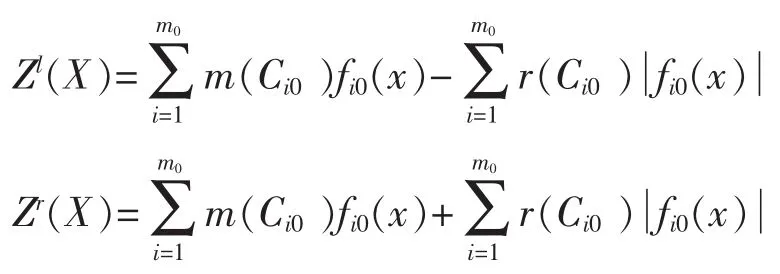
在解决问题的过程中,决策者可以根据自己的偏好灵活选择排序函数z=f(x,y)
例6考虑下面的问题

解:设z=f(x,y)为I(R)上的排序函数,则问题转化为
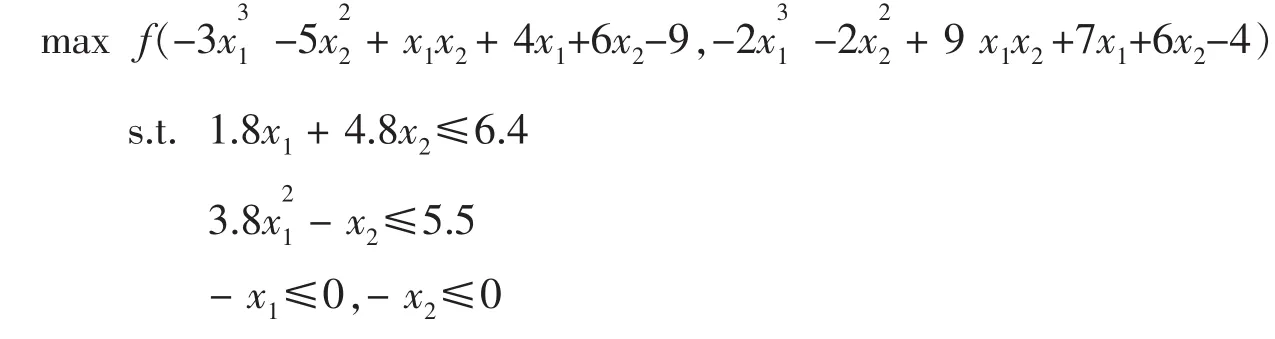
取排序函数为f(x,y)=ax·by,(a>1,b>1),不妨a=1.1
当b=1.05时,排序函数为保守型排序,求得最优解为[-6.0992,13.8236].
当b=1.1时,排序函数为折中型排序,最优解为[-6.4300,14.0625].
当b=1.15时,排序函数为风险型排序,最优解为[-6.6268,14.1463].
下表给出了b取不同值时,最优解的情况:

表4 .1 a=1.1,b取不同值时,原优化问题的最大区间数的取值情况
从以上结果可以看出,风险型排序注重右端点的最大化程度较大,随着b的增大,这种程度变大;保守型排序风险型排序注重左端点的最大化程度较大,随着b的减小,这种程度变大;以上折中型排序的结果即为中点最大。
5 结论与展望
本文首先总结了区间数的排序方法,提出了区间数排序函数的概念,研究了排序函数的分类方法和相关性质。然后,将区间数排序函数应用于区间数非线性规划问题的求解中,利用排序函数将其转化为普通的优化问题。最后,通过例子说明了决策者可根据自己的需要选择排序函数来解决区间数的优化问题。对区间数排序函数还可以继续进行更加细致的分类和研究,这将有利于决策者选择更合适的排序函数解决问题。
[1]刘进生,王柱绪.区间数排序[J].工程数学学报,2001,18(4):103-109.
[2]刘华文.基于距离测度的模糊数排序[J].山东大学学报,2004,39(2):30-36.
[3]李霞,张绍林,张淼,刘华.基于新距离测度的区间数排序[J].西华大学学报,2008,27(1):87-90.
[4]刘新旺,达庆利.一种区间数线性规划的满意解[J].系统工程学报,1999,14(2),123-128.
[5]郭均鹏,吴育华.区间线性规划的标准型及其求解[J].系统工程,21(3),79-82,2003.
[6]胡宝清.区间目标规划与模糊目标规划[J].模糊系统与数学,2004,18:218-223.
[7]蒋峥,戴连奎,吴铁军.区间非线性规划问题的确定化描述及其递阶求解[J].系统工程理论与实践,2005,(1):110-116.
[8]Alefeld R,Herzberger J.Introduction of interval computations.Academic Press,New York,1983.
[9]R.E.Moore,Method and Application of Interval Analysis,SIAM,Philadelphia,1979.
[10]Ishibuchi H,Tanaka H.Formulation and analysis of linear programming problem with interval coefficients[J].Journal of Japan Industrial Management Association,40(5),320-329,1989.
[11]侯勇超,曹炳元.一种区间系数非线性规划的模型与求解方法[A].中国运筹学会第八届学术交流会论文集,2006.
Abstract:In this paper,the definition of ordering function is proposed.First,we study its properties and classification.Next, the ranking function is used to solve interval nonlinear programming problems by converting them to classic ones.Finally,an example illustrates the feasibility and simplicity of the method.
Key words:Interval Number;Ranking Function;Nonlinear Programming
责任编辑:宏彬
STUDY OF INTERVAL COEFFICIENT NONLINEAR PROGRAMMING BASED ON RANKING FUNCTION
HOU Yong-chao1ZHAO Kai-bin1QIU Hai-quan2
(1Department of Mathematics,Chaohu University,ChaohuAnhui238000)
(2College of Science,Anhui Scoence and Technology University,Fongyang Anhui 233100)
O159
A
1672-2868(2010)03-0005-06
2010-02-23
巢湖学院基金项目(项目编号:XLY-200903),安徽省教育厅重点项目(项目编号:KJ2010A242)。
侯勇超(1982-),男,山东聊城人,助教,研究方向:模糊优化,数值方法。
