非织造布的结构特征与其吸声性能研究

杨 树于伟东潘 宁，2

(1.东华大学纺织学院软物质研究中心，上海，201620; 2.加州大学戴维斯分校，美国加州戴维斯，95616)

非织造布的结构特征与其吸声性能研究

杨 树1于伟东1潘 宁1，2

(1.东华大学纺织学院软物质研究中心，上海，201620; 2.加州大学戴维斯分校，美国加州戴维斯，95616)

测试了不同非织造布的透气性能和吸声性能，并对几种吸声理论进行了对比分析。测试数据说明:非织造布的透气性不只是简单地与孔隙率成正比，还与其他一些复杂的不易测量的参数有关;非织造布在测试频段的吸声曲线随背面空气层的增厚而向低频域移动;材料的孔洞特征，特别是平均孔径是影响共振吸收峰频率的主要参数。

非织造布，孔洞特征，透气性能，吸声性能，共振吸收峰

非织造布是典型的纤维类吸声材料，有关其吸声性能的研究已有很多报道［1-3］。Zwikker等［4］将多孔介质看作空气相和固体物质相两相的混合物，两相对于声波的反应作用不同。Shoshani等［5］利用Zwikker等人的理论，计算了一些在人耳可听的频域内能够产生很好吸声效果的非织造布的内在特征数据。事实上，非织造布的隔音性能与其结构有着密切的关联。有研究表明，纤维的密度、形状和长度在吸声隔音中是非常重要的因素［6-7］。Tascan等［8］研究了针刺非织造布的密度和表面面积对吸声性能的影响。Voronina［9］通过实验得到一个模型，用以预测多层纤维的吸声系数和声阻，前提只要纤维的直径和密度已知。

本文对几种非织造布的结构参数及其透气性能和吸声性能进行了实验表征，并对纤维介质背面有无空气层时的吸声性能做了比较。

1 实验

1.1 基本结构参数测试

(1)厚度。使用南通宏大集团制造的YG141N型

式中:m——样品质量;

A——样品的截面积;

L——样品厚度;

ρ——样品中的纤维密度。

1.2 透气性能测试

使用南通宏大集团制造的YG461E型数字式织物透气量仪测定样品的透气性能，测试过程符合GB/T 5453—1997标准。样品两端压力差设置为200 Pa，测试面积为20 cm2;喷嘴直径是在测试过程中根据样品的透气性能进行选择，透气性能越好的样品需要匹配的喷嘴越大，透气性能差的样品则匹配小的喷嘴。数字式织物厚度仪测量样品的厚度，测试过程符合ISO 5084:1996标准。测量选取压力为50 cN，加压时间为10 s。

(2)面密度。使用千分位电子天平测量半径为15 mm的圆形样品的质量，计算得到样品的面密度。

(3)孔洞特征。使用美国PMI公司制造的CFP-1100-A毛细管流动孔径仪测试非织造布的孔洞尺寸分布，计算得到孔洞平均直径。

样品的孔隙率(ε)定义为空气的体积(Va)与材料总体积(VT)的比值，可以由下式计算得到:

1.3 吸声性能测试

材料的吸声系数有两种常用的测试方法:混响室法(GB/T 20247—2006)和驻抗管法。本实验采用后者，因为该方法需要的样品量比较少，同时其测试系统采用垂直入射声波，使测试更快更精确。在驻抗管法中也有两种方法可以选择:驻波比法(GB/T 18696.1—2004)和传递函数法(GB/T 18696.2—2002)。两者的区别在于传递函数法是由固定在管壁上的两个传声器代替了驻波比法的一个滑动传声器，从而使测试范围更大，因此选用传递函数法。本实验选用声望技术有限公司制造的SW260型双传声器驻波管测试系统，测试过程符合GB/T 18696.2—2002和 ISO 10534-2:2001标准。其结构示意见图1。

图1 SW260型双传声器驻波管测试系统示意

由于测试过程使用的是平面波，波长比测试管直径大，故选择最细管径30 mm的测试管进行测试。在测试过程中应特别注意两个传声器的匹配。

传递函数法的基本原理是，通过测量样品前两个传声器之间的传递函数H12可以得到声波的法向反射系数r。传递函数H12为复数，定义式为［10］:

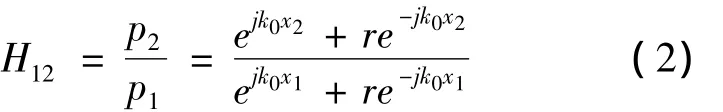
其中 k0——波数，k0=2πf/c0

式中:p1，p2——分别是两个传声器处的复数声压; x1，x2——分别为两个传声器距离参考面(x=0)的距离;

f——声频;

c0——声速。

入射声波的传递函数HI和反射声波的传递函数HR，可以通过下式计算:

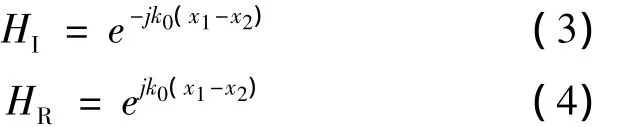
结合公式(2)～(4)，可以得到法向反射系数r:

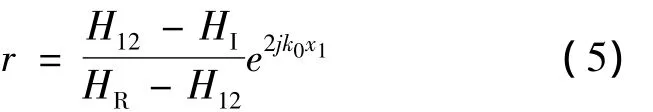
通过r可以得到吸声系数α的表达式:

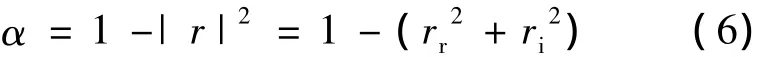
式中:rr，ri——分别表示r的实部和虚部。

2 结果与讨论

2.1 基本结构参数

表1为6块非织造布样品基本结构参数的测试结果。图2为毛细管流动孔径仪测得的样品的孔径分布情况。

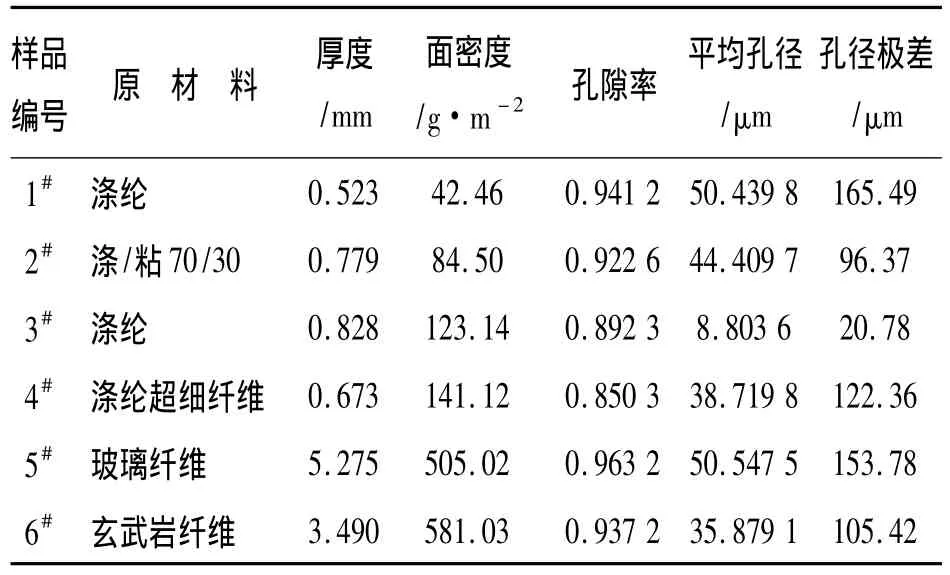
表1 样品的基本结构参数

2.2 透气性能

根据苛仁纳公式，材料的理论透气系数 Ktfp(cm2/Pa·s)为［11-13］:

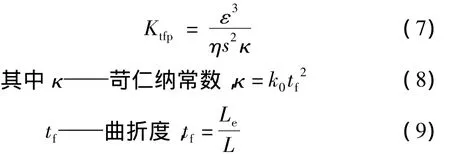
式中:ε——样品的孔隙率;

η——流体黏度(Pa·s);

s——润湿通道表面(1/cm);

k0——形状因子;

Le——有效通道长度或样品有效厚度(cm);

L——样品厚度(cm)。

Mohammadi［14］利用Davies透气常数kD［11］改

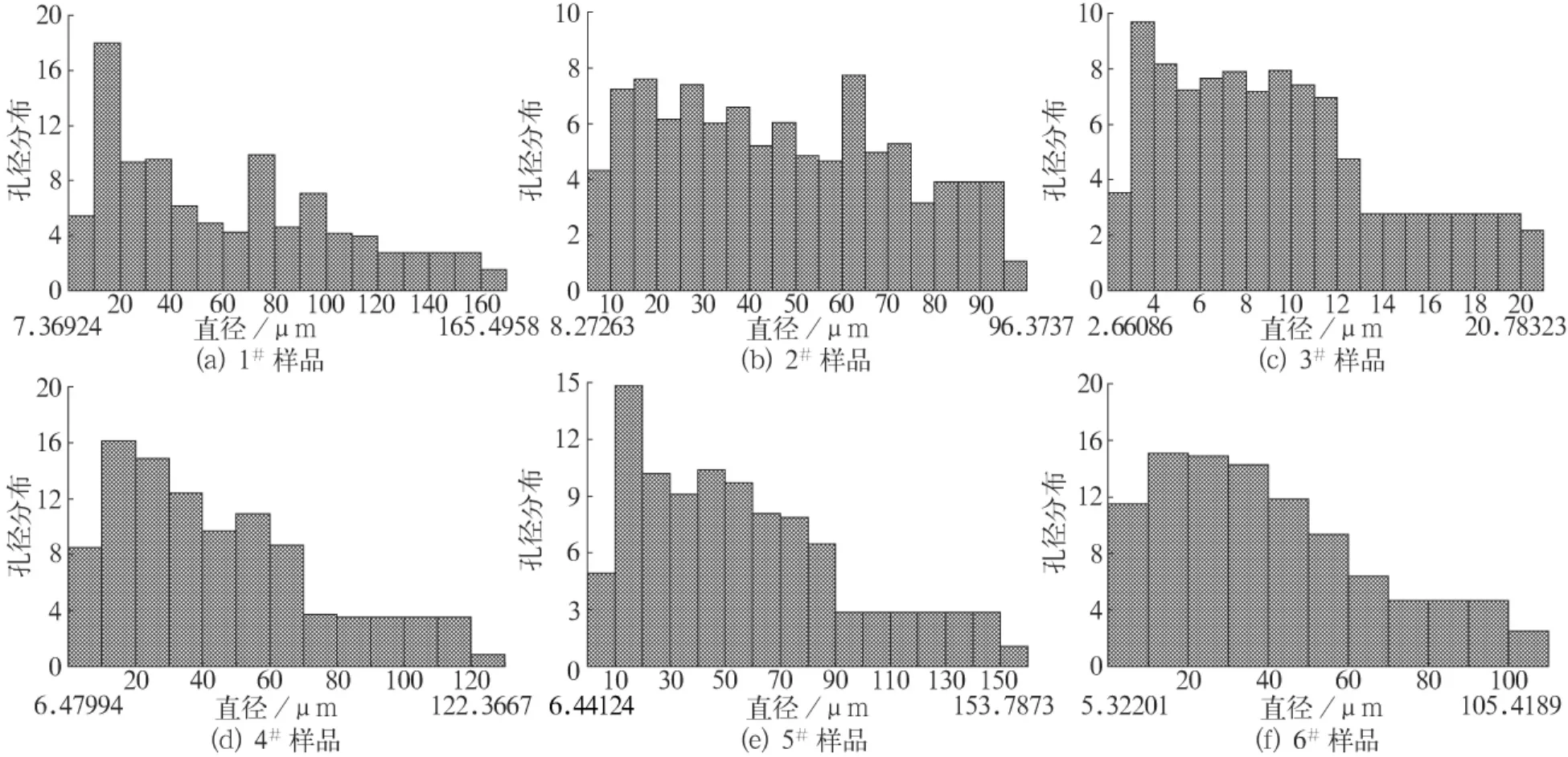
图2 非织造布样品的孔径分布

进了苛仁纳公式，得到了纤维结构材料孔隙率在0.94～0.994范围内的理论透气率qtp(cm/s):

式中:d——纤维直径(cm);

Δp——样品两端的压差(Pa)。

Davies透气常数kD的定义为:

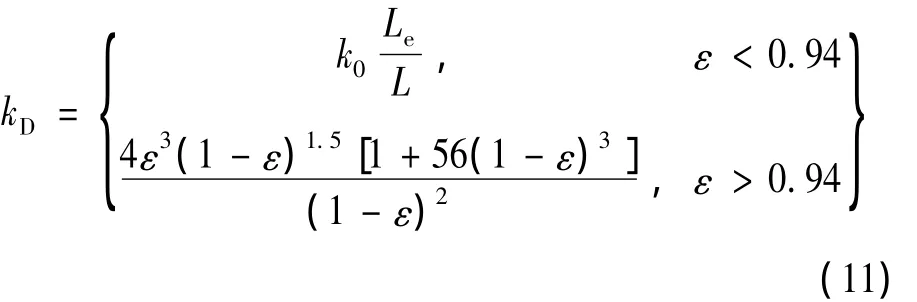
公式(10)显示样品的透气率不只简单地与孔隙率成正比关系，还与很多参数有关，其中有些是不易测量的参数，如曲折度、形状因子等。

图3 非织造布样品的透气率

图3是6块非织造布样品的透气性能测试结果，3#和6#样品的透气性能较差。对照表1中样品的基本结构参数，可以发现3#样品具有最小的平均孔径，6#样品次之，因此可以肯定，孔径也是影响非织造布透气性能的重要参数之一。

2.3 吸声性能

分别测试了样品在背面没有空气层(刚性壁)、有15 mm空气层和30 mm空气层三种情况下的吸声系数，结果示于图4。

图4(a)是样品背面为刚性壁时的吸声曲线。对照表1中样品的基本结构参数，可知此时材料的吸声系数基本随着样品厚度的增加而提高，其中1#～4#样品的厚度值差别不大。

图4(b)是样品背面有15 mm空气层时的吸声曲线。与无空气层时比较，空气层的引入大大提高了材料在该段测试频域上的吸声效果，吸声曲线初始上升的速率也有大幅提高。

图4(c)是样品背面空气层增大到30 mm时的吸声曲线。与图4(b)相比较，可以看到增厚的空气层使得材料的吸声曲线初始段上升的斜率变大，从而使得吸声峰值向低频域移动。

3 几种吸声理论的对比分析

3.1 毛细管吸声理论

早期的研究大都是以毛细管理论［15］来解释多

图4 非织造布样品在三种不同背面情况下的吸声系数

式中:z——声阻率;

L——材料厚度(m);

η——空气黏度，为1.85×10－5Pa·s;

a——孔洞等效半径(m);

ε——孔隙率;

ρ0c0——空气特征阻抗，为413 km/(m2·s)。

很明显，公式(12)在计算声阻率时并没有考虑频率问题，而实际上声阻率是随着频率而变化的。由于声阻率和吸声系数成正比，因此对理论声阻率和实验得到的两组吸声系数值进行了比较。一组是整个测试频域上的平均吸声系数，另一组是共振频率处的最大吸声系数。对比结果示于图5。可以看到，最大吸声系数值与理论声阻率值有相近的变化趋势。

3.2 穿孔板共振吸声理论

考虑到非织造布的结构与带有微孔的板类似，尝试用穿孔板的共振吸声理论来解释其共振频率［16］。穿孔板共振吸声结构是噪声控制中广泛采用的吸声装置，设穿孔均匀地分布在板上，各个穿孔的大小和形状完全相同。若穿孔板的穿孔率为σ，板后空气层的厚度为D，穿孔的有效长度为l，则该结构的共振频率f可按下式计算:

孔材料的吸声性能。在该理论中，材料的吸声性能与材料厚度、孔径和孔隙率有关。相对声阻抗率(以下简称声阻率)可以下式计算:

式中:c0——空气中的声速。

l在穿孔率较大时可近似为板厚。

按公式(13)计算，可以得到6块样品的共振频率大小的顺序为5#<6#<3#<2#<4#<1#，然而实验得到的共振吸声峰对应的频率大小顺序为3#<6#<5#<4#<2#<1#。实验结果说明，穿孔板共振吸声结构不能很好地解释非织造布的吸声峰频率问题。

图5 声阻率(理论值)与最大吸声系数(实验值)的比较

3.3 膜振动理论

考虑到所测非织造布样品的厚度较小，故可以将其视作膜材料。膜振动理论是将样品看成一块薄膜，其吸声机理主要是膜的共振吸收，当声波频率等于其固有频率时达到共振吸声系数。张新安［17］曾提出应用膜振动理论计算多孔吸声材料的声阻抗，然而仍忽略了频率这一关键因素。如果将非织造布样品看作一块薄膜，应用膜振动理论，则膜上的波速c为:

式中:w——膜的面密度;

T——膜的表面张力。

对于半径为R膜的圆形薄膜，其固有频率f为:

实验中的6块试样，其施加的表面张力T基本相等，而其面密度的顺序是1#<2#<3#<4#<5#< 6#。根据公式(14)和(15)计算，得到样品的固有频率排序为6#<5#<4#<3#<2#<1#。实验得到的共振吸声峰对应的频率大小顺序为3#<6#<5#< 4#<2#<1#，可以看出3#样品比较特殊，查看其基本结构参数，其原因可能是3#样品具有最小的孔径(8.803 6 μm)和较低的孔隙率(0.892 3)。

由以上分析可见，膜共振理论并不能完全解释纤维集合体的吸声行为，因为有许多因素影响着集合体的吸声效果。

3.4 吸声行为涉及的几个参数

弄清楚材料吸声模型中各因素的作用，对于材料的优化设计有着至关重要的意义。然而，纤维材料的优化设计非常复杂，这是由于许多影响因素之间不是互相独立的［18］。

图6和图7分别是样品的吸声峰频率和最大吸声系数的直方图。对照表1中样品的基本结构参数，包括材料的面密度、厚度、孔隙率和平均孔径(其中面密度和厚度是有交叉关联的参数)进行直观比较。从比较结果可以看到，影响材料共振吸收峰对应频率的参数主要是材料的孔洞特征参数，特别是样品的平均孔径;影响材料最大吸声系数的参数是厚度、孔径和孔隙率等，与前述毛细管吸声理论讨论的结果基本一致。

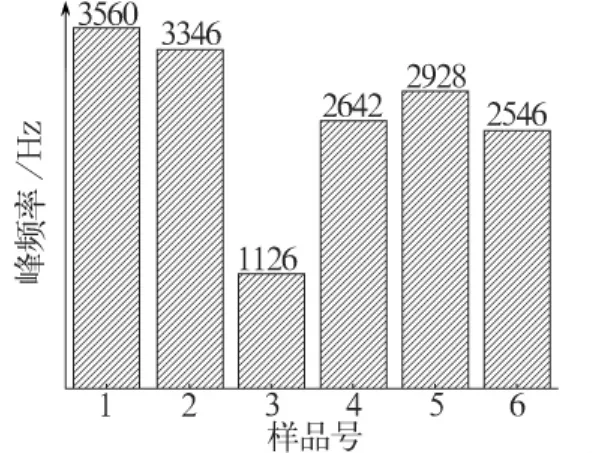
图6 吸声峰频率直方图

图7 最大吸声系数直方图

4 结论

(1)通过对非织造布样品透气性能的实验结果和苛仁纳公式的分析，可以得出纤维集合体的透气性能不仅是简单地与孔隙率成正比，还有一些复杂的不易测量的参数也会对其有影响，如样品孔洞通道的曲折度、形状因子等。

(2)对非织造布背面为刚性壁和有空气层时进行的吸声实验证明，空气层的引入大大提高了材料在测试频域的吸声性能;增厚样品背面的空气层会使材料在该段的吸声曲线初始段上升的斜率变大，同时吸声曲线整体向低频域移动。

(3)非织造布的背面分别为刚性壁和空气层时，其吸声机理可能有所不同。对于刚性壁的情况，非织造布的吸声系数随着样品厚度的增加而增大;而有空气层时其影响因素则更为复杂，涉及到样品的孔洞特征等参数。传统的毛细管吸声理论基本可以解释吸声系数值的问题，但是没有考虑到频率因素;应用膜振动理论来解释非织造布的吸声频率，也有个别样品实验值与理论不符。

(4)通过直观比较最大吸声系数值和吸声峰频率及其样品的几个结构参数，认为影响材料共振吸收峰频率的参数主要是材料的孔洞特征，特别是样品的平均孔径。

［1］ SHOSHANI Y.Effect of nonwoven backings on thenoise absorption capacity of tufted carpets［J］.Textile Research Journal，1990，60(8):452.

［2］ SHOSHANI Y.Studies of textile assemblies used for acoustic control tech［J］.Textiles Int，1993，2(3):32-34.

［3］ SHOSHANI Y，ROSENHOUSE G.Noise insulating blankets made of textile［J］.Applied Acoustics，1992，35(2):129-138.

［4］ ZWIKKER C，KOSTEN C W.Sound absorbing materials［M］.London:Elsevier，1949.

［5］ SHOSHANI Y，YAKUBOV Y.Numerical assessment of maximal absorption coefficients for nonwoven fiberwebs［J］.Applied Acoustics，2000，59(1):77-87.

［6］ BALLAGH K O.Acoustical properties of wool［J］.Applied Acoustics，1996，48(2):101-120.

［7］ NARANG P P.Material parameter selection in polyester fiber insulation for sound-transmission and absorption［J］.Applied Acoustics，1995，45(4):335-358.

［8］ TASCAN M，VAUGHN E A.Effects of total surface area and fabric density on the acoustical behavior of needlepunched nonwoven fabrics［J］.Textile Research Journal，2008，78(4):289-296.

［9］ VORONINA N.Improved empirical model of sound propagation through a fibrous material［J］.Applied Acoustics，1996，48(2):121-132.

［10］HAN F S，SEIFFERT G，ZHAO Y Y，et al.Acoustic absorption behaviour of an open-celled aluminium foam［J］.Journal of Physics D-Applied Physics，2003，36 (3):294-302.

［11］CAMAN P C.Flow of gases through porous media［M］. Butterworths Scientific Publications，1956.

［12］CLARENBURG L A，PIEKAAR H W.Aerosol filters: I-theory of the pressure drop across single component glass fibre filters［J］.Chem Eng Sci，1968，23(7):765-771.

［13］PIEKAAR H W，CLARENBURG L A.Aerosol filters——the tortuosity factor in fibrous filters［J］.Chem Eng Sci，1967，22(12):1817-1827.

［14］MOHAMMADI M，BANKS-LEE P，GHADIMI P.Air permeability of multilayer needle punched nonwoven fabrics:theoretical method［J］.Journal of Industrial Textiles，2002，32(1):45.

［15］ALLARD J F.Sound propagation in porous media: modelling sound absorbing materials［M］.London: Elsevier，1993.

［16］赵松龄.噪声的降低与隔离(上册)［M］.上海:同济大学出版社，1985.

［17］ZHANG X A.Applying of membrane vibration theory for sound absorption study of thin fiber layers［J］.Journal of Shaanxi Normal University(Natural Science Edition)，2006，34(6):25-27.

［18］DINSMORE M.Acoustical material modeling parameter sensitivities［C］//In SAE Noise＆ Vibration Conference.USA，2009.

Study on texture character and acoustic absorbent behavior of nonwovens

Yang Shu1，Yu Weidong1and Pan Ning1，2

(1.College of Textiles＆Center of Soft Materials，Donghua University;2.Biological and Agricultural Engineering Department，University of California)

The permeability and acoustical properties of several nonwovens were measured，and then various theories of sound absorption were compared.The results showed that the permeability of nonwovens is not just linear to porosity，but also related with other factors.Increasing air gap behind nonwovens moves the absorption curve towards lower frequency.Pore characteristic especially mean pore size is proved to be the most effective factor that influences absorption peak frequency.

nonwovens，pore characteristic，permeability，acoustic absorption property，resonant peak shift

TS171

A

1004－7093(2010)07－0006－06

2010－02－01

杨树，女，1985年生，在读博士研究生。主要研究方向为纤维集合体的结构特征与其吸声性能的关系。