正态吸引场非平稳NA列部分和的精确渐近性
2010-09-07王张燕王文胜
曾 艳,王张燕,王文胜
(杭州师范大学理学院,浙江杭州310036)
正态吸引场非平稳NA列部分和的精确渐近性
曾 艳,王张燕,王文胜*
(杭州师范大学理学院,浙江杭州310036)
令{Xi:i≥1}是正态吸引场非平稳NA序列,Sn=∑ni=1Xi,得到了正态吸引场非平稳NA列部分和Sn的精确渐近性的结果,揭示了拟权函数和边界函数之间的密切联系.同时将已有的一些结果包含成为特殊情形.
非平稳;正态吸引场;NA序列;部分和;精确渐近性
0 引 言

设0<α≤2,Ga(x)是非退化α阶稳定分布,{X,Xi:i≥1}为独立同分布随机变量序列,称X属于Ga的吸引场,如果存在常数列{an:n≥1}和正数列分别称为中心化常数和正则化因子.由文[4]推论2.2.17知,如果0<α≤2,X属于Ga的正则吸引场当且仅当

其中c1,c2为非负数且c1+c2>0.
文[3]得到了关于正态吸引场强平稳NA序列如下一个结论:

其中Z~N(0,σ2).
关于精确渐近性理论的研究,以往的结果都附加有强平稳条件的限制,而在许多实际问题中所出现的NA序列大多都是非平稳的,故解除强平稳条件的束缚具有较大的理论和实际意义.该文研究了正态吸引场非平稳NA序列的精确渐近性.首先考察非平稳同分布NA序列的情形.
1 主要结果
文[5]提出了NA序列的概念.
定义1 称随机变量X1,X2,…,Xn,n≥2是NA(Negative A ssociation)的,若对∀n≥2,{1,2…,n}的任何两个非空不交子集A1,A2,均有Cov(f1(Xj:j∈A1),f2(Xk:k∈A2))≤0,其中f1,f2是任何两个对每个变元不减且使上式有意义的函数.称随机变量列{Xi:i≥1}是NA列的,若对∀n≥2,X1,X2,…, Xn是NA的.

这里Z是服从正态分布N(0,σ2)的随机变量,{bn:n≥1}是满足条件的正数列.
注1 定理将文[3]中强平稳NA序列的结果包含在内,事实上强平稳序列中的条件σ2=EX21+蕴涵了条件(i);另外由强平稳性,对任意的正整数m和n,Sn和Sm,n具有相同的分布,由文[6]知存在满足条件(ii)的序列{nk:k≥1}.
注2 该文对g(x)附加了条件(2)、(3)、(4)的限制.但函数g(x)也足以包含令人感兴趣的函数类.特别地,取r=2,g(x)=x或g(x)=lnln x时,该定理分别将独立场合下的式(1)及文[7]建立的对数律的精确渐近性所包含,故该文的结果更为宽泛.
定理2 设ρ≥0,0
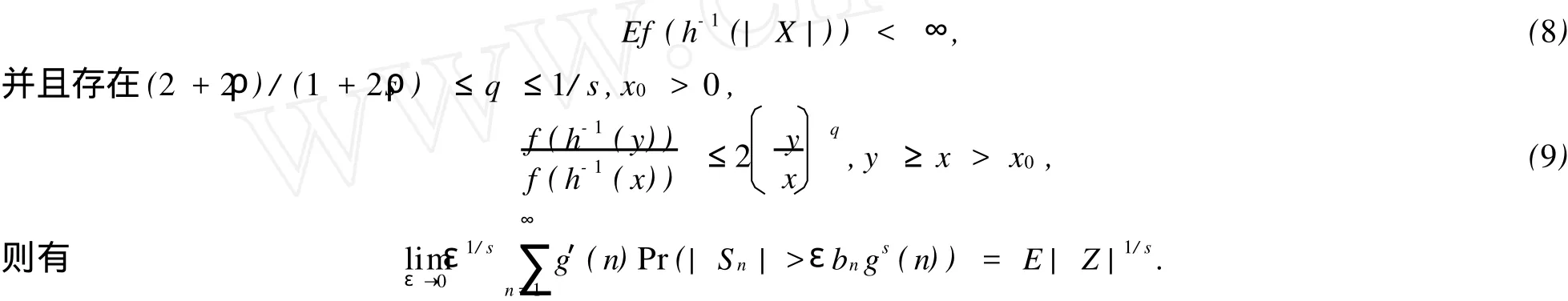
其中bn同定理1,h-1(·)表示h(·)的反函数.
注3 文[3]中定理3的结果是这个定理的特殊情形.
2 定理的证明



3 非同分布情形的结果
[1]Heyde C C.A supplement to the strong law of large numbers[J].J Appl Prob,1975,12:173-175.
[2]Wang Yuebao.On asymp totic fo r class of small parameters sequencesof B-value dependent random variables[J].Acta Math App le Sinica,1995,18(3):344-352.
[3]Cheng Fengyang,Wang Yuebao.Precise asymptoticsof partial sums for IID and NA sequences[J].Acta Mathmatica Sinica.Chinese Series,2004,47(5):965-972.
[4]Embrechts P,Kluppelberg C,Mikosch T.Modelling extremal events for insurance and finance[J].Eerlin:Springer,1997,20(4):200-214.
[5]Joag-dev K,Proschan F.Negative association of random variables with applications[J].Ann Statist,1983,11(1):286-295.
[6]苏淳,迟翔.非平稳NA序列中心极限定理的一些结果[J].应用数学学报,1998,21(1):9-21.
[7]Gut A,Spataru A.Precise asym totics in the law of the iterated logarithm[J].Ann Probab,2000,28(4):1870-1883.
[8]Liu Lixin,Wu Rong.Inequalites of maximal partial sum and the law iterated logarithm for sequencesof NA random variables[J].Acta Math Sinica,2002,45:969-978.
Precise Asymptotic in Partial Sums of Normal Attraction Nonstationary NA Sequence
ZENG Yan,WANG Zhang-yan,WANGWen-sheng
(College of Science,Hangzhou Normal University,Hangzhou 310016,China)
Let{Xi:i≥1}be the no rmal attraction nonstationary NA sequence,letthe paper obtains the result of the p recise asymp totics in partial sums of normal attraction nonstationary NA sequence as well as Sn,and reveals the close relation between weighted function and boundary function,the result includes some know n theorems as special cases.
nonstationary;no rmal attraction;NA sequences;partial sum;p recise asymptotic
O211.4 MSC2000:60F15;60E15;60E05
A
1674-232X(2010)03-0204-05
DO I:10.3969/j.issn.1674-232X.2010.03.009
2009-11-03
国家自然科学基金项目(10771070).
曾 艳(1976—),女,浙江黄岩人,应用数学专业硕士研究生,从事概率极限理论研究.
*通讯作者:王文胜(1970—),男,浙江杭州人,教授,博士生导师,主要从事概率极限理论研究.E-mail:w swang@yahoo.cn
