证券市场套利模型及应用研究
2010-09-07陈溟
○陈溟
(内蒙古科技大学数理与生物学院 内蒙古 包头 014010)
证券市场套利模型及应用研究
○陈溟
(内蒙古科技大学数理与生物学院 内蒙古 包头 014010)
本文研究了在证券市场中单因素影响下的套利模型和双因素影响下的套利模型,并在证券市场中就套利模型的应用进行了分析,为投资者进行决策提供了有效的分析方法。
套利模型 单因素模型 双因素模型
与投机相比,套利具有其独特的优势,因此有必要对套利模型进行深入探讨。从长期来看,证券收益率存在较多的影响因素,这些影响因素和证券收益率之间又存在纷繁复杂的关系;从中短期来看,证券收益率的影响因素相对较少,并且比较容易辨别其影响程度的强弱。因此,为了便于对套利模型进行研究,及时捕捉套利机会,本文仅研究周期为两周的短期套利模型。
一、单因素的套利模型
假设证券i的期望收益率与某一因素存在一定的相关关系。设该影响因素为F,则得到模型:

其中,ri为预期收益率,βi为影响因素F的敏感系数。设其他的影响因素极其微弱,即εi=0,则有方程:

公式(2)中,当F=0时,则得ri=αi=rf,也就是无风险收益率,它是一个固定的常数。只要能够准确地估计出每支股票对影响因素F的敏感程度βi,若F的值是可以量化的,就可以根据公式(2)算出预期收益率ri;若因素F是定性的,则可以根据敏感程度,由主观判断来估计预期收益率ri。
如果存在这样一种股票组合,投资者无需追加资金,组合风险为0,收益率大于0,则形成可套利的股票组合,这时就为套利行为打开了方便之门。设Δxi为持有第i种股票的改变量,若投资者只持有三支股票,则套利股票组合必须同时满足以下三个条件(假设不考虑套利的交易费):

根据公式(3)中的前两个条件,可以得出无穷多组解。因此可以任取Δx1=m,则由公式(3)前两个条件有:

由公式(4)可得:
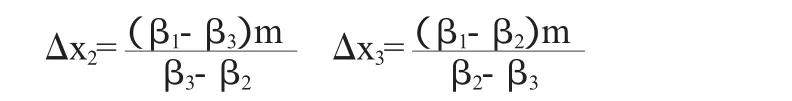
将Δx1,Δx2,Δx3的值代入公式(3)中的第3个方程得:

若(5)式成立,则反映出三种股票的组合没能达到均衡,也就意味着存在套利机会。
投资者只要对变动量为负的股票做空头,而对变动量为正的股票做多头,这样可以再无需追加资金又不冒任何风险(若非因素风险很小)的情况下获利。

表1 三支股票的相关资料
假设三种股票的预期收益率和影响因素F的敏感系数如表1所示,那么投资者三支股票的组合是否存在套利机会呢?三支股票的预期收益率与因素敏感度构成的散点图中,出现的三点明显不在同一条直线上,也就是说,根据散点图,可以大致估计出股票组合没有达到均衡状态,因此可以判定存在套利机会。若不考虑套利行为产生的交易费用,则可以根据表1资料得出:
我们就这样在乡里唯一的,也是最繁华的“长安”大街上走着,在目光织成的网中穿过,似乎还听见了窃笑声。我想溜,又没借口,想跑又跑不起来,只好低下头,感到芒刺在背,苦不堪言。我斜眼见她挺着丰满、高耸的胸脯潇洒自若地走着,想和我说什么;我佯装看脚下的路,只看见她一闪一闪,穿着白皮凉鞋的脚尖。

再设Δx1=6,由方程组

解得:Δx2=-11;Δx3=5。
将Δx1=6,Δx2=-11,Δx3=5代入公式(6)中的第3个式子得:

(8)式是成立的,见表2:

表2 投资者的套利结果
由表2可知,投资者通过减持股票B而获取的11万元资金用于购买6万元的股票A和5万元的股票C,股票变动量的净额为0,而投资者的股票总市值仍然保持60万元,既不增加投资,又不承担风险,只要预期收益率能够实现,就可以套取1.06万元的现金收益。这也反映了股票A与股票C被市场低估,而股票B被高估,股票组合未能达到均衡状态。随着套利行为的不断继续,股票B因供过于求而遭到大量的抛售,从而导致股价下降,预期收益率逐渐上升;股票A和股票C因供不应求,致使大量资金涌入,股价纷纷抬升,预期收益率逐渐下降,此时宣布套利行为结束。
上面的三支股票的改变量是任意设定的。现在来分析一般情况:设Δx1=m,代入公式(6)的前两个式中得:

解得:Δx2=-1.83m,Δx3=0.83m。现将Δx1=m,Δx2=-1.83m,Δx3=0.83m代入公式(6)的第3式中得:

在现实中,套利行为也存在交易费,在证券市场上买卖股票,都必须要交纳交易手续费(交易金额的0.3%)和印花税(交易金额的0.2%)。因此(3)式就变成:

(11)式中,0.5%为交易手续费和印花税系数,它是按交易金额来计算的。同理,设Δx1=m,代入公式(11)中的前两个方程求得:
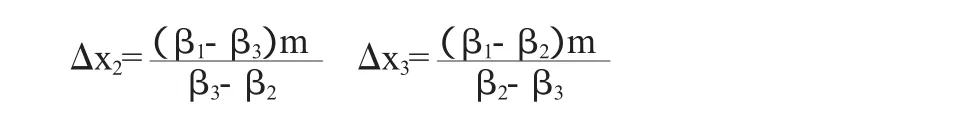
将Δx1,Δx2,Δx3的值代入公式(11)中的第3个方程中得:

只要(12)式成立,就有套利机会。设交易手续费和印花税为0.5%,(6)式就变成:

设Δx1=m,由(13)式可以解得Δx2=-1.83m,Δx3=0.83m,将3个改变量代入(13)式中第3个方程可得:

由(14)式可以得到与不考虑交易费时相同的结论,即只要改变量m为正数,就存在套利机会,并且随着改变量m的增大,套利收益也逐渐增大。在理论中,改变量m不受限制,使套利收益可以趋于无穷大,但在现实的证券市场中,改变量m是受限制的,同样为1.83m≤20,解得m≤10.91万元。也就是说,股票A的最大改变量只能达到10.91万元,在考虑交易费时,最大的套利收益为1.75万元。
因此,投资者为了获取最大的套利收益,可以通过卖空预期收益率低的股票,而购进预期收益率高的股票,一旦实现预期的收益率,便可以获得套利收益。
二、双因素模型
假设在短期内存在两个影响较大的因素,分别设为F1,F2,其他的因素影响极其微弱,则得到模型:

其中,β1i,β2i分别为影响因素F1,F2的敏感系数。αi是无风险收益率。若影响因素F1,F2的值是可以量化的,就可以根据公式(15)算出预期收益率ri;若因素F1,F2是定性的,则根据敏感程度,由主观判断来估计预期收益率ri。
在证券市场中,套利通常需要考虑交易费。因此,在有交易费时,双因素影响下的套利条件为:

令Δx1=m,代入(16)式的前两个等式中得:

由(17)式解得:

将Δx1,Δx2,Δx3的值代入(16)式中的第3式中,得出:

只要上面的不等式成立,就存在套利机会。
由于在短期内对股票的影响因素相对较少,因此在进行套利分析时,通常采用单因素模型和双因素模型。而对于影响因素可能多于两种的情况,则可以采取筛选的方法,选择影响最大的两个因素,利用双因素模型来进行研究。投资者持有的股票组合可能多于三支,投资者只需将所有股票分成若干种三支股票的组合,利用单因素模型和双因素模型进行分析后,寻找最佳的套利组合来进行套利。
三、结论
总之,套利相对于投机者来说是一种相对新型的谋利方式,这种方式不仅风险相对较小(有时甚至无风险),而且还可以谋取利润。相对于风险较大的市场,套利技术的应用无疑是投资者最有利的选择。但要真正掌握好套利技术,不仅对影响因素要有准确的估计,还要敏锐地把握住时机,这一切尤其需要大量的实战经验作为坚实的后盾。
应该说,套利定价模型仅仅是一个模型而已,它对实践的拟合程度再高,模型设定得再合理,也只是一个近似的概念,不可能做到百分百的复制。实践中,我们不能期望应用某个神奇的模型而获利丰厚。“套利”为“投机”设置了极限,国外专业投资基金几十年、上百年的业绩分析报告也证明了这一点。理论要为实践服务,理论是实践的指导,理论本身就是宝贵的精神财富,理解、认识套利定价模型不仅可以填补在认识领域中的空白,也让我们在实践中更主动、更沉稳。
[1]哈姆·勒威、马歇尔·萨纳特著,陈云贤、朱敢林译:证券投资组合与选择[M].中山大学出版社,1995.
[2]黄良文:投资估价原理[M].北京科学出版社,2002.
[3]叶永刚:金融工程概论[M].武汉大学出版社,2000.
[4]王涛明:证券投资风险计量、预测与控制[M].上海财经大学出版社,2003.
(责任编辑:李文斐)
book=7,ebook=155
