关于非线性Petrovsky方程初边值问题的注记
2010-09-07张有珍王书彬
张有珍, 王书彬
(1.郑州轻工职业学院基础部 河南郑州450002;2.郑州大学数学系 河南郑州450001)
关于非线性Petrovsky方程初边值问题的注记
张有珍1, 王书彬2
(1.郑州轻工职业学院基础部 河南郑州450002;2.郑州大学数学系 河南郑州450001)
考虑一类具有非线性阻尼项和源项的Petrovsky方程的初边值问题,通过对稳定集和非稳定集的精确刻画,证明了当初值属于稳定集及其边界时问题整体弱解的存在惟一性.
Petrovsky方程;初边值问题;稳定集;整体弱解
0 引言
非线性Petrovsky方程是描述梁振动问题的一类重要的四阶波动方程,并且出现在许多物理问题中[1-2].本文考虑具有非线性阻尼项和源项的Petrovsky方程的初边值问题,
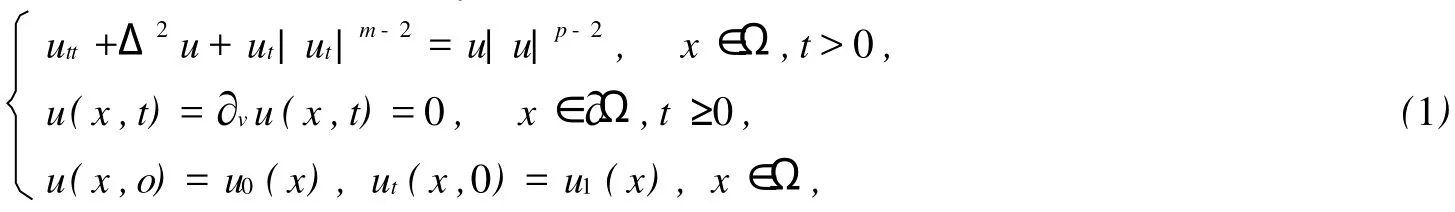
其中,m≥2,p≥2,Ω是Rn中的一个具有光滑边界∂Ω的有界区域,v是∂Ω的单位外法向量.
Messaoudi[3]对问题(1)进行了研究,证明了当m≥p时,初边值问题的弱解是整体存在的,当m 在本文中使用如下记号:Hk(Ω)=Wk,2(Ω)表示Sobolev空间,(Ω)={w∈H2(Ω):0},其中和是在迹的意义下取值.分别表示Lp(Ω)和H2(Ω)的模,特别地 首先给出初边值问题(1)的局部存在性定理. 定理1[3]假定当n≤4时,2≤m<∞,2 (Ω),u1∈L2(Ω),则对某个足够小的T>0,初边值问题(1)存在惟一弱解 且对t∈[0,T],有 定理1使(1)在Ω×[0,T)上存在解的所有T的上确界称为问题(1)解的生命界,用T*表示.如果T*=∞,称解是整体的;如果T*<∞,称解是非整体的,此时也称解在有限时刻发生爆破,利用标准的延拓方法可以证明. 定理2在定理1的条件下,若 为了刻画稳定集和不稳定集,引入泛函 引理1设2)J(λu)对λ∈[0,+∞)有惟一的极值点,且在λ0处取到最大值 引理2设,u≠0,记 引理31)若I(u)<0,则;2)若;则I(u)>0;3)若I(u)>0,则0<;4)若,则I(u)<0. 引理4若J(u)≤d,则1)I(u)>0的充要条件是2)I(u)<0的充要条件是 定理3记(Ω):‖Δu‖ 证明1)只需证明⊂W.当时,,从而J(u),当u≠0时,0≤,故知u∈W,即⊂W;2)若,则I(u)=0,J(u)≤d,且u≠0,因此u∈N,且J(u)≤d,故得u∈E*,反之,若u∈E*,则J(u)=d,I(u)=0,因此. 引理5在定理1的假设下,若E(0) 引理6在定理1的假设下,若E(0) 定理4在定理1的假设下,若E(0)≤d,m 证明首先,从定理1可知问题(1)存在惟一的局部解u(x,t),记解u(x,t)的生命界为T*,只需证明T*=∞. 引理1设(Ω),u≠0,则1)=0,=-∞;2)J(λu)对λ∈[0,+∞)有惟一的极值点λ0=,且在λ0处取到最大值. 引理2设u,记 取序列{λk}使得0<λk<1,k=1,2,…,且当k→∞时λk→1,令u0k=λku0,u1k=λku1,考虑初边值问题 如果u1=0且u0=0,则Ek(0)=0 且 利用引理6有估计式 于是由引理3和引理4可知 从式(5)和(6)可知,存在惟一函数~u∈W~和{uk}的子序列(仍记为{uk})使得对任意的T>0,当k→∞时uk在L∞(0,T;)中弱*收敛于,ukt在L∞(0,T;L2)中弱*收敛于,ukt在Lm((0,T)×Ω)中弱*收敛于在L∞(0,∞);中弱*收敛于 在等式(4)中,令m=k→∞可得 显然有~u(x,0)=u0(x),~ut(x,0)=u1. 因此~u是初边值问题(1)的整体弱解,从问题(1)解的惟一性可知在且对任意的故得T*=∞.定理证毕. [1] Reed M,Simon B.Methodsof Modern Mathematical Physics,in:Scattering Theo ry[M].3rd Edition.New Yo rk:Academic Press,1979. [2] Zauderer E.Partial Differential Equations of App lied Mathematics,in:Pure and Applied Mathematics[M].2nd Edition. New Yo rk:a Wiley-Interscience Publication,1989. [3] Messaoudi SA.Global existence and nonexistence in system of Petrovsky[J].J Math Anal App l,2002,265:296-308. [4] Messaoudi S A.Global existence and decay of solutions to a system of Petrovsky[J].J Math Sci Res,2002,6(11): 534-541. [5] Chen Wenying,Zhou Yong.Global nonexistence fo r a semilinear Petrovsky equation[J].Nonlinear Analysis:Theo ry, Methods&App lications 2009,70(9):3203-3208. [6] 韩献军,薛红霞.一类具有非线性阻尼和源项的Petrovsky方程的初边值问题解的存在性和渐近性[J].高校应用数学学报,2008,23(2):153-158. [7] 尹丽,薛红霞,韩献军.一类具有非线性阻尼和源项的Petrovsky方程的初边值问题解的爆破[J].数学实践与认识, 2010,40(4):168-174. Remark on the Initial Boundary Value Problem for Nonlinear Petrovsky Equation ZHANG You-zhen1, WANG Shu-bin2 The initial boundary value p roblem is studied for Petrovsky equation w ith nonlinear damping and source term s.By construsting the stable set and the unstable set,the existence and the uniqueness of global weak solution are p roved w hen the initial value belongs to the stable set and it's boundary. Petrovsky equation;initial boundary p roblem;stable set;global weak solution O175.13 A 1671-6841(2010)03-0031-03 2010-03-12 国家自然科学基金资助项目,编号10971199;河南省基础与前沿技术计划项目,编号08230041060. 张有珍(1964-),女,讲师,主要从事非线性微分方程研究,E-mail:zhangyouzhen0816@126.com.1 预备知识
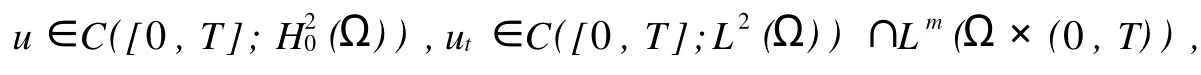

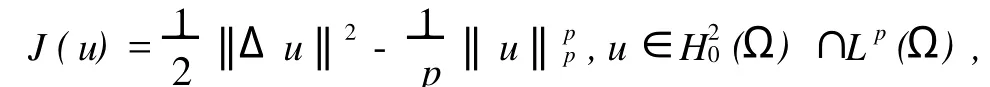
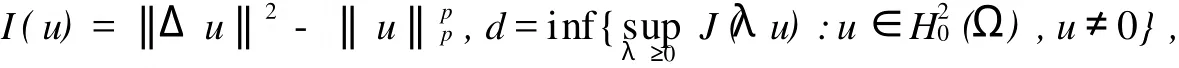
2 整体解的存在性

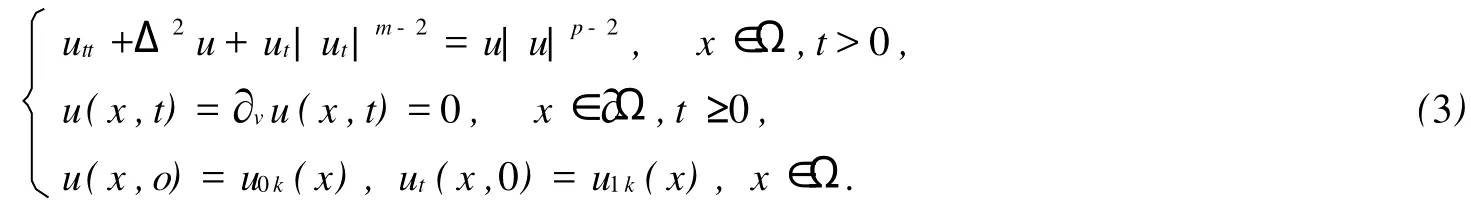

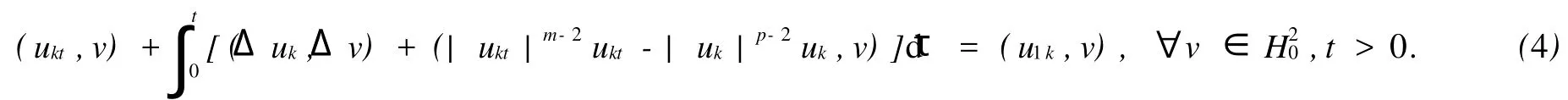
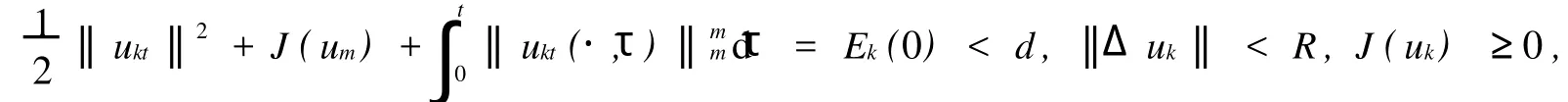
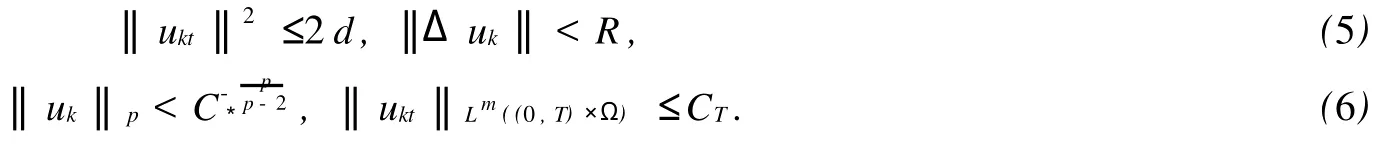
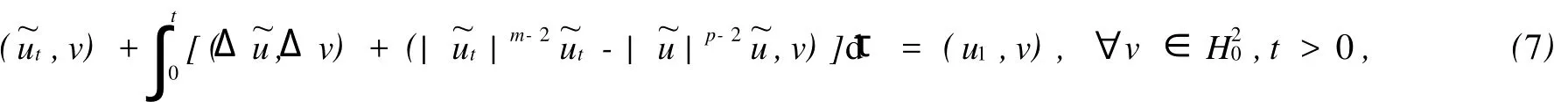
(1.Department of Foundation,Zhengzhou Vocational Colloge of L ight Industry,Zhengzhou 450002,China;2.Department of M athem atics,Zhengzhou University,Zhengzhou 450001,China)
