一个类似Burgers方程的数值解

盛秀兰, 艾 尧, 吴宏伟

(1.东南大学数学系 江苏南京210096;2.江苏广播电视大学公共课教学部 江苏南京210036)

一个类似Burgers方程的数值解

盛秀兰1,2, 艾 尧1, 吴宏伟1

(1.东南大学数学系 江苏南京210096;2.江苏广播电视大学公共课教学部 江苏南京210036)

研究了一个类似Burgers方程的初边值问题的有限差分方法.基于Crank-Nicolson方法,建立了一个两层线性化隐式差分格式,讨论了差分格式的可解性.利用离散能量估计方法证明了差分解在最大模意义下关于时间和空间的二阶收敛性,并用数值算例验证了理论分析结果.

类似Burgers方程;隐式差分格式;收敛性;离散能量估计

0 引言

考虑初边值问题[1]:

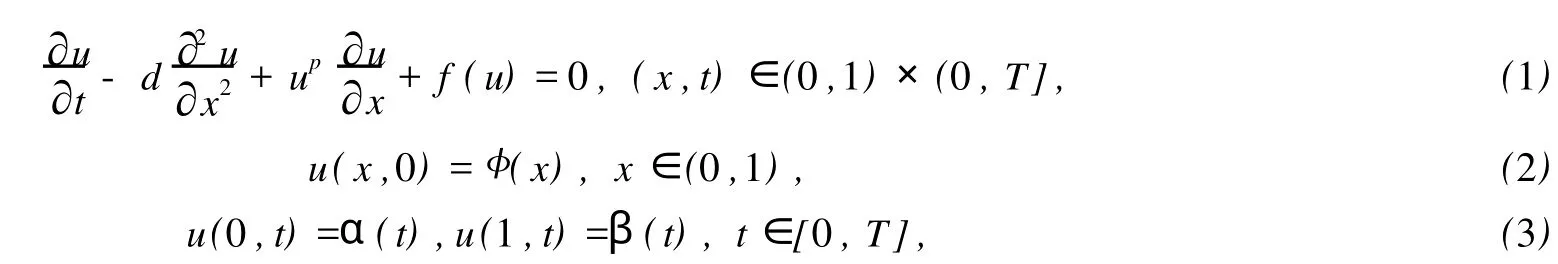
其中,p=1,2,d>0为粘性常数,f(u)是非线性函数,φ(x),α(t),β(t)为已知光滑函数,且满足相容性条件.

当p=1且f(u)≡0时,方程(1)成为著名的Burgers方程,有很多文献研究了该问题的数值解法.可以通过Hop f-Cole变换将方程化为一个标准的热方程,然后用高阶差分格式求解[2-4].但是当f(u)≠0时,此方法不再适用.文[5]研究了当f(u)≡0时保持能量守恒的差分格式,但当f(u)非零时能量不再守恒.文[6]给出了一个线性化的差分格式,该格式的截断误差是O(τ+h2),但文中没有给出理论分析结果.

通过分析以上文献,正如[3]指出的,当p=1且f(u)=0,如果对方程(1)直接用差分逼近,得到的线性化格式一般关于时间的精度是1阶的,要得到关于时间是2阶的格式,如用Crank-Nicolson格式,通常格式是非线性的或者是3层以上格式.其原因主要是非线性项uux的线性化离散问题.当带有非线性强迫项后,要构造关于时间2阶收敛的线性化两层格式显得更为困难.

本文研究当p=2时初边值问题(1)～(3)的线性化差分解法.构造了一个关于时间和空间2阶收敛的线性化两层差分格式.在处理非线性项f(u)的时候,采用与文献[11]类似的方法,而对非线性项u2ux的逼近,提出了一种新的离散方法.证明了差分格式解的存在唯一性和收敛性.给出了差分格式的解在离散最大模意义下收敛阶数为O(τ2+h2).最后给出了两个数值算例,计算结果显示本文提出的方法是有效的.

本文假设:

H1问题(1)～(3)存在唯一光滑解,且存在常数C0,使得对有

H2函数f二阶可导,且存在正常数C1,δ,使得当,有

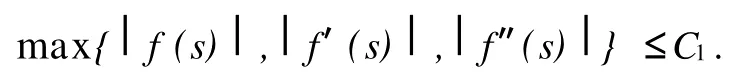
1 记号及差分格式

取正整数m,n,记h=1/m,τ=T/n,xi=ih,0≤i≤m,tk=τk,0≤k≤n.定义Ωh={xi|0≤i≤={(xi,tk)|0≤i≤m,0≤k≤n}.设{|0≤i≤m,0≤k≤n}为Ωhτ上的网格函数,引进记号:

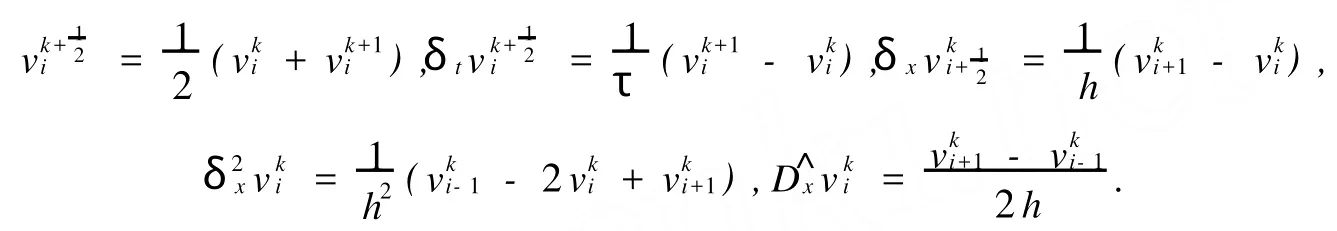
我们构造初边值问题(1)～(3)的差分格式为:

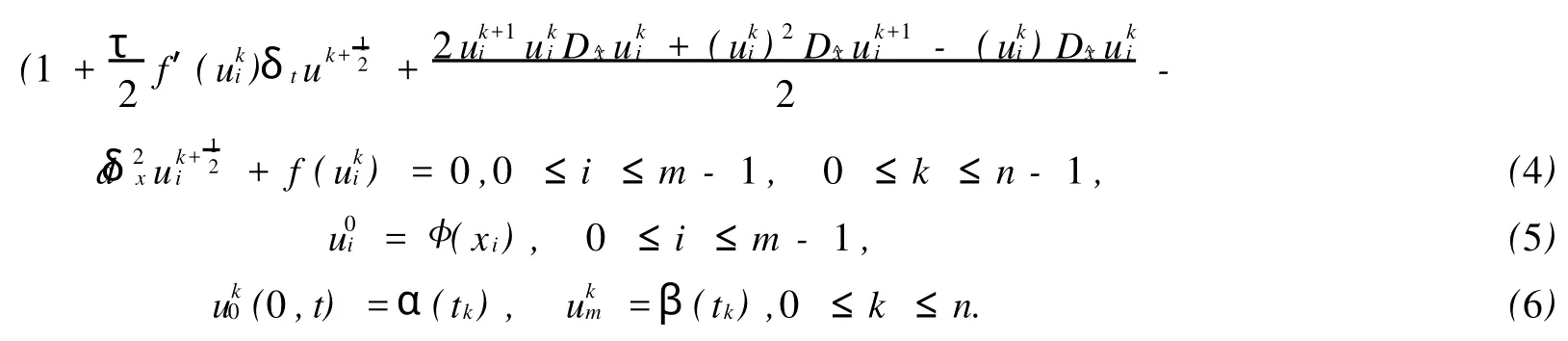
差分格式(4)～(6)是一个两层线性化的差分格式,对每一固定的时间层k,差分方程的系数矩阵是3对角矩阵,可以用追赶法求解.

2 差分格式的可解性和收敛性

引理1[12-13]设v,w∈Vh,则有

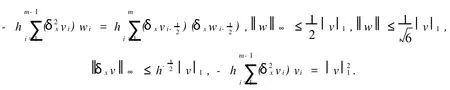
下面的引理2是离散非线性项u2ux的关键.

引理2设函数u(t),v(t),w(t)∈C2[0,T],记.则

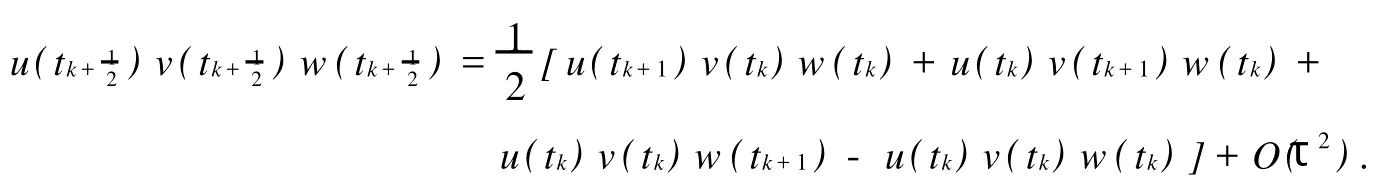
证明记p(t)=(uvw)(t),则由Taylor展开及向前差商得

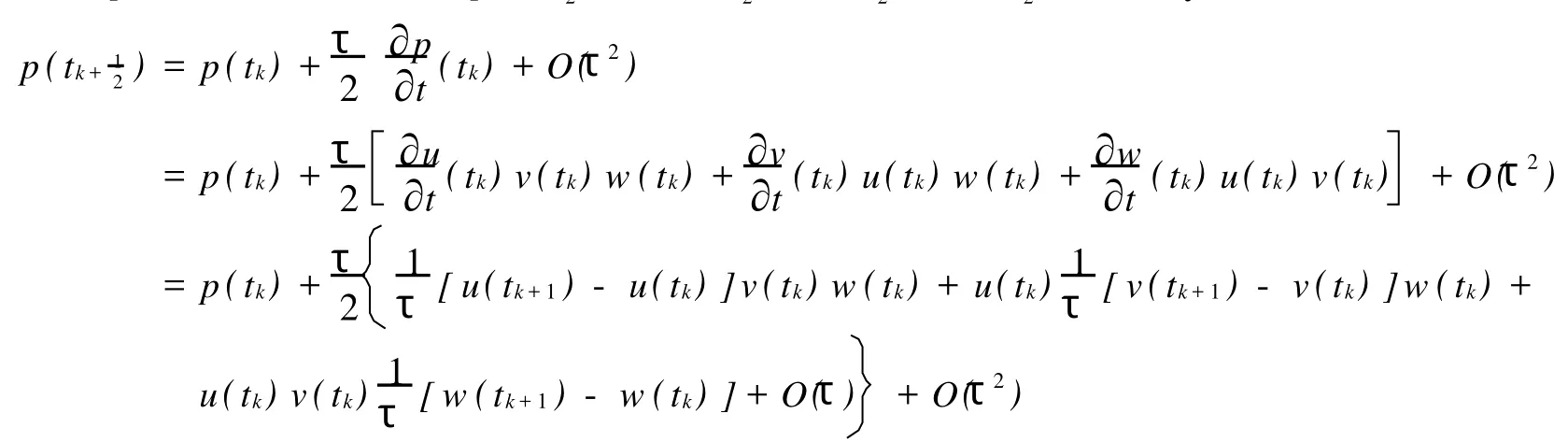
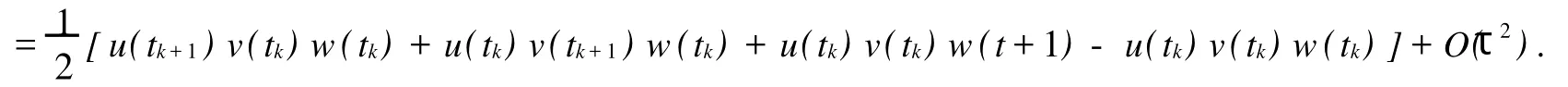
引理2证毕.

利用引理1和引理2以及能量估计和数学归纳法,可以得到下面的收敛性估计.

定理1设u(xi,tk)是问题(1)～(3)的解,满足差分方程(4)～(6),记,如果φ(x)∈ C[0,1],且存在常数C0>0,使得,则当h,τ充分小且时,有

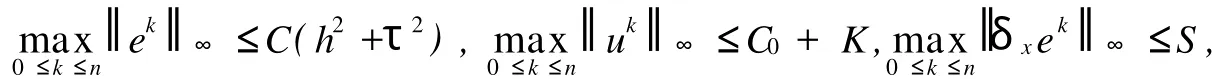
其中,C>0,K>0,S>0是与h,τ无关的常数.

由定理1可知,当步长h,τ充分小时,对固定的k,差分格式(4)～(6)的系数矩阵严格对角占优,因此有下面的结论.

定理2当步长h,τ充分小,差分格式(4)～(6)存在唯一解.

3 数值试验

利用差分格式(4)～(6)计算2个实例,计算结果见表1和表2.

例1

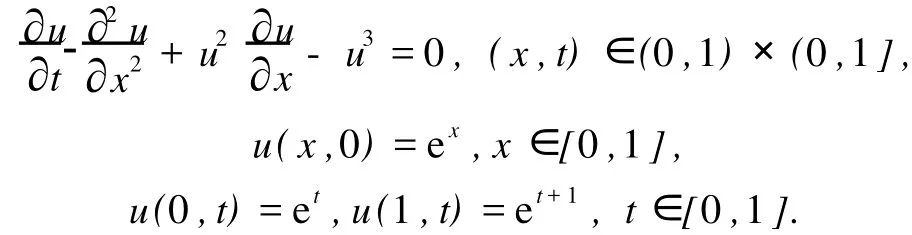
该问题的精确解为ex+1.

例2

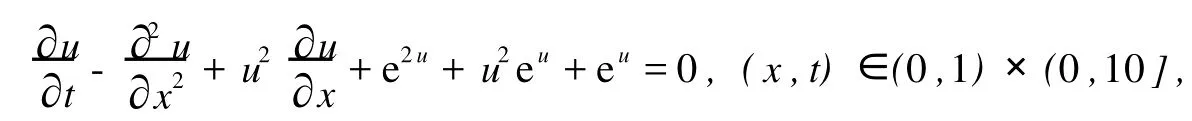
表1 例1的不同步长下的误差和收敛阶数Tab.1 Errorsandconvergencerateaboutthefirstexample

表2 例2的不同步长下的误差和收敛阶数Tab.2 Errorsandconvergencerateaboutthesecondexample

[1] Bülent S,˙Idris D.A numerical study of the Burgers’equation[J].J Franklin Institute,2008,345(4):328-348.

[2] Brander O,Hedenfalk J.A new formulation of the general solution to Burgers’equation[J].Wave Motion,1998,28 (4):319-332.

[3] Liao Wenyuan.An imp licit fourth-order compact finite difference scheme fo r one-dimensional Burgers’equation[J].App l Math Comput,2008,206(2):755-764.

[4] Yousuf M.On the classof high order time stepping scheme based on Padé’s app roximations for the numerical solution of Burgers’equation[J].App l Math Comput,2008,205(1):442-453.

[5] Anguelov R,Djoko J K,Lubuma JM S.Energy p roperties p reserving schemes fo r Burgers equation[J].Numer M ethods Partial Differential Equations,2008,24(1):41-59.

[6] Kutluay S,Esen A.A linearized numerical scheme for Burgers-like equations[J].App l Math Comput,2004,156(2): 295-305.

[7] Djoko J K.On the long-time stability of a backward Euler scheme fo r Burgers’equation w ith polynomial force[J].Numer Methods Partial Differential Equations,2008,24(6):1371-1387.

[8] Lewandow ski J L V.A markermethod for the solution of the damped Burgers’equation[J].Numer Methods Partial Differential Equations,2006,22(1):48-68.

[9] 孔令江,张超英,谭惠丽,等.用格子Boltzmann方法模拟kdv-Burgers方程的激波解[J].广西师范大学学报:自然科学版,2003,21(4):1-4.

[10] 洪宝剑,卢殿臣,张大珩.带强迫项变系数组合kdv-Burgers方程的显式精确解[J].广西师范大学学报:自然科学版, 2007,25(1):17-20.

[11] 吴宏伟.二维半线性反应扩散方程的交替方向隐格式[J].计算数学,2008,30(4):349-360.

[12] 孙志忠.偏微分方程数值解[M].北京:科学出版社,2004.

[13] Zhou Yulin.App lication of Discrete Functional Analysis to the Finite Difference Method[M].Beijing:International Academic Publishers,1990.

Numerical Solution of a Burgers-like Equation

SHENG Xiu-lan1,2, A I Yao1, WU Hong-w ei1
(1.Department of M athem atics,Southeast University,N anjing 210096,China; 2.D ivision of Public Course,Jiangsu Radio and TV University,N anjing 210036,China)

A second-order finite difference scheme for a Burgers-like equation is p roposed and analyzed.The scheme constructed is a double-deck linearized scheme that can be solved easily by Thomas’algo rithm.The solvability of difference scheme is obtained.It is show n that the difference scheme is convergent in maxim um no rm.The convergence o rder is second-o rder in bo th space and time.Some numerical experiments are conducted to illustrate the theoretical results of the p resented method.

Burgers-like equation;imp licit difference scheme;convergence;discrete energy estimate

O 241.82

A

1671-6841(2010)03-0023-04

2009-11-25

国家自然科学基金资助项目,编号10871044.

盛秀兰(1976-),女,讲师,主要从事微分方程数值解研究,E-mail:113525336@qq.com.