含缺陷混凝土的弹性模量预测

姚 婷,杜成斌,孙立国

(1.江苏博特新材料有限公司,江苏南京 210008;2.河海大学力学与材料学院,江苏南京 210098)

混凝土是由粗骨料、细骨料、水泥水化物、未水化水泥颗粒、孔隙及裂纹等组成的非均质复合材料[1]。其宏观力学性能非常复杂,以往主要通过试验方法得到[2]。但试验周期长,耗费的物力和人力多,得出的结论与试验条件及所选取的材料都有很大关系,并具有一定的随机性,且大多侧重于宏观尺度上的研究,忽略了混凝土内部细观结构的高度复杂性与非均匀性,所以难以揭示混凝土材料的变形或者破坏机理,尤其是在载荷作用下,随机分布的微裂纹、孔洞及骨料界面等这些混凝土试件中天然存在的大量细微观缺陷的扩展对混凝土性能的影响。细观力学方法[3-4]正是基于混凝土的这些特性,对细微观结构的特性及其各种缺陷的不均匀性与混凝土宏观力学性能之间的关系进行研究。

如何预测微裂纹损伤材料的有效弹性模量是脆性材料细观损伤理论的一个重要内容。目前已经有很多学者进行了这方面的研究,如赵爱红等[5]将损伤张量定义为含缺陷时的弹性模量与不含缺陷时的弹性模量的比值,来研究含正交排列缺陷混凝土弹性模量的估算方法,其关键是对含缺陷的弹性模量进行估算。目前除了Taylor方法或稀疏估计方法(它们完全忽略了缺陷之间的相互作用),还有考虑微缺陷相互作用的方法:Mori-Tanaka方法[6]、自洽方法[7]、广义自洽方法[8]和微分法等[9],而关于裂纹间的相互作用机制,其他研究者做了比较细致的研究[10-16]。

任何材料的宏观力学行为和性能与材料内部的微细观组织结构有着十分紧密的关系。混凝土的构造和内部构成相当于事物的内因,而它的宏观力学性能受微细观结构的制约,且宏观上的破坏也是由微细观上的断裂和损伤行为的发展和累积造成的,所以如何从微细观结构的力学性质预测宏观的力学性能(如弹性模量)已成为该领域研究的重要工作。前述混凝土参数预测方法过程复杂,其中还需要求解一些非线性方程,且这些方法本身存在很多假设,不方便应用,所以有必要研究新的预测含缺陷混凝土的弹性模量方法。笔者在文献[17-18]的基础上,在体积表征单元中加入缺陷相,运用细观力学数值均匀化方法研究混凝土复合材料的弹性模量,在此基础上对各影响参数的敏感性进行分析。

1 数值方法预测含缺陷混凝土的弹性模量

1.1 随机骨料数值模型的建立

将圆形孔隙或币状裂隙作为缺陷,将混凝土视为由骨料、砂浆和界面组成的三相复合材料,把原始缺陷看成混凝土的另一组成相反映在混凝土数值模型中,即把圆形孔隙和币状裂隙分别看作一相材料反映在混凝土数值模型中,在二维随机骨料模型[19]基础上加入缺陷相,生成的随机骨料如图1所示。同时采用渐进网格法剖分单元,在不影响计算精度的前提下,尽量减少单元数目。典型的模型及网格剖分如图2所示。

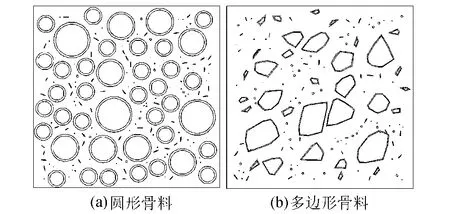
图1 随机骨料模型

图2 随机骨料模型网格剖分示意图

1.2 数值均匀化方法

从混凝土中取1个体积表征单元(RVE),即特征体积单元,该单元包含混凝土中具有的结构缺陷、砂浆、骨料及砂浆与骨料之间的界面等信息,能够反映混凝土宏观力学性能。从宏观上来讲,它足够小,其应力场可看作是均匀的;从细观上来讲,它足够大,包含了要考虑的足够多的细观结构信息,可以体现出材料的统计平均性。为了计算混凝土的有效弹性模量,笔者应用细观力学数值均匀化方法对混凝土体积表征单元施加如下均匀位移边界条件:

式中:ui为对应节点位移边界条_件的参数;ε0ij为平均应变矩阵ε0的分量,取 ε0,其中 ε为已知应变常数,若混凝土受拉则 ε为正,反之为负;xj为某节点的坐标。

根据上述均匀位移边界条件,就可以通过有限元方法计算求得y方向上各个单元的应力和应变,再通过式(2)和式(3)计算模型上的平均应力σ和平均应变ε,混凝土的弹性模量可以通过式(4)计算得到。

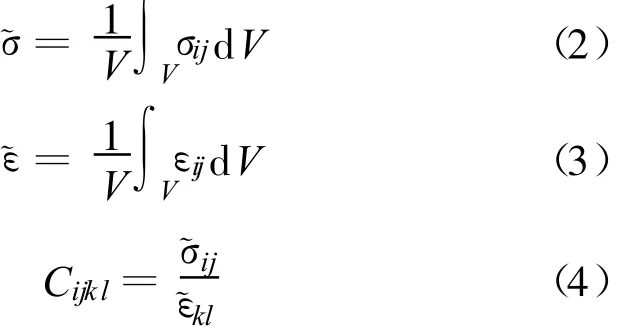
式中:V为混凝土的体积;Cijkl为混凝土的有效弹性模量矩阵的分量。

式(2)(3)(4)即为用平均场理论得到的混凝土有效弹性模量。它是基于周期性体积表征单元在每个单元上的加权平均。为了简化计算,仅考虑二维平面应力问题,并假定混凝土各相材料同性。为了更方便简洁地得到混凝土的有效弹性模量,笔者根据式(2)(3)(4),编制Fortran语言程序,使其可以直接计算出混凝土材料的弹性模量,简化了后处理过程。

1.3 混凝土宏观弹性模量的试验验证

1.3.1 各组分的材料参数选取

计算模型中材料参数选用Stock试验结果[20]:骨料最大粒径为19mm,最小粒径为0.15mm,各组分的材料参数见表1。由于界面过渡层的厚度不足0.1mm,限于目前计算机的计算能力,以及网格划分的困难,模拟中界面厚度的取值相对过大,此处界面厚度取为0.2mm,骨料的形状采用圆形或多边形。

1.3.2 二维平面上骨料体积分数的计算

骨料的粒径分布可用骨料的颗粒分布曲线表示。为产生优化的混凝土的结构密度和强度,可以采用Fuller级配曲线,但是由Fuller级配曲线得到的是骨料在混凝土中的空间分布情况,本文仅考虑混凝土的二维数值模拟,因此需将三维级配曲线转化为二维平面级配曲线,即将空间球状骨料模拟转化为平面圆形骨料模拟。Walraven等[21]基于概率统计的原理将三维Fuller骨料级配曲线转化为二维平面级配曲线,得到试件内任一截平面上的骨料直径D小于筛孔直径D0的概率为

表1 混凝土各组分的材料参数

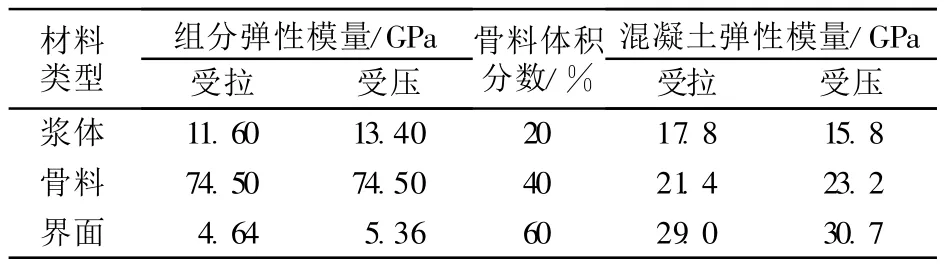
材料类型组分弹性模量/GPa 混凝土弹性模量/GPa受拉 受压骨料体积分数/%受拉 受压浆体 11.60 13.40 20 17.8 15.8骨料 74.50 74.50 40 21.4 23.2界面 4.64 5.36 60 29.0 30.7

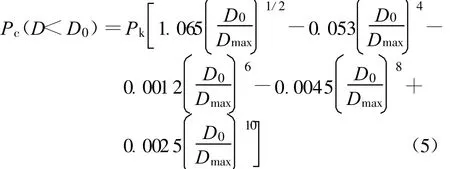
式中:Pk为骨料体积占试件总体积的百分比,即骨料的体积分数;Dmax为最大骨料粒径。

由式(5)根据不同的D0值可以得到概率分布曲线Pc(D＜D0)～D0/Dmax,这样即可求得在任一试件截平面上各级骨料粒径的颗粒数目。

1.3.3 计算模型

这里体积表征单元尺寸取为0.1m×0.1m,分别求出骨料体积占20%,40%,60%时平面内所包含的骨料颗粒数。为方便起见,粒径小于3mm的骨料计入砂浆。

首先,根据前文所述方法生成混凝土随机骨料数值模型,对于不同的骨料体积分数各生成3个体积表征单元,并对含缺陷混凝土及不含缺陷混凝土模型划分网格。然后进行材料属性判别:当单元节点均落在骨料颗粒内时,定为骨料单元,并赋予其骨料材料属性;当单元节点均落在骨料和砂浆界面层区域内时,则定为界面单元,并赋予其界面材料属性;当单元节点均落在硬化水泥砂浆区域内时,定为砂浆单元,并赋予其砂浆材料属性。以上材料类型的识别与赋值都是由计算机自动实现。最后,给该试件的左端面施加水平方向的约束,右端均布施加水平方向的单轴受拉或受压位移荷载,用位移控制加载,加载位移为0.01mm。计算简图如图3所示。

图3 试件单轴计算简图

1.3.4 计算结果

通过数值计算,得到含缺陷(根据文献[22],将缺陷体积分数取为1.5%)和不含缺陷时混凝土的有效弹性模量,计算结果见表2和表3,表中Va表示混凝土骨料体积分数。

表2 含缺陷时混凝土的有效弹性模量 GPa

表3 不含缺陷时混凝土的有效弹性模量 GPa

从表2和表3可以看出,采用本文提出的模型,混凝土有效弹性模量的预测结果均小于或等于试验值,这可能是因为Stock试验的最小骨料粒径为0.15mm,而由于投放时的困难,本文考虑的最小骨料粒径为0.3mm,况且对于界面弹性模量的取值也只是根据文献资料,并没有准确的试验数据。从表2～3可以看出除了受拉时Va=20%时的预测结果与试验值相差很大外,其他误差值均在3%～9%。从含缺陷和不含缺陷的情况对比来看,含缺陷时混凝土的有效弹性模量比不含缺陷时稍小,这是因为在含缺陷情况下混凝土试件内部容易产生应力集中现象,会弱化混凝土的宏观力学性能。从整体来看,混凝土受压试件的弹性模量预测结果比受拉试件的好,这与砂浆和骨料的弹性模量试验值有很大关系。从不含缺陷时的情况来看,无骨料时(Va=0),其弹性模量预测值与试验值一样;而含骨料时(Va≠0),预测值普遍比试验值小,这也符合一般认识。Va=20%时误差较大,笔者认为与试验结果有关,因为从其他体积分数下的试验结果来看,其受压弹性模量均比受拉情况下大,而Va=20%时却相反,此问题值得进一步探讨。

2 混凝土细观结构参数对有效弹性模量的影响

利用有限元方法研究混凝土细观结构参数对宏观弹性模量的影响,材料参数选取文献[23]中的试验数据,即水泥浆弹性模量Ep=31GPa,骨料弹性模量Ea=65GPa,界面弹性模量Ei=28GPa,水泥浆基体泊松比 νp=0.18,骨料泊松比 νa=0.15,界面泊松比 νi=0.31;界面厚度取0.2mm;模型中缺陷体积分数取1.5%。以下所有的计算过程均是单轴受压情况下的结果。

2.1 最大骨料粒径对混凝土有效弹性模量的影响

首先讨论最大骨料直径对混凝土有效弹性模量的影响。分别设最大骨料粒径Dmax=8mm,16 mm和32mm,其他参数保持不变,骨料体积分数Va分别取20%,30%,40%,50%,计算结果如图4所示。从图4可以看出,对于给定的骨料体积分数,混凝土有效弹性模量随着Dmax的增大而增大,但幅度并不大,这是因为界面体积分数随着Dmax的增大而减小,总体而言,界面在整个混凝土组分中占非常小的比例。如对于Va=40%的混凝土,骨料直径分别为8mm,16 mm和32 mm时,界面体积分数分别占3.1%,1.5%和0.8%,而且本身界面弹性模量就比骨料和混凝土的都小。所以最大骨料粒径对混凝土有效弹性模量的影响不大。

图4 最大骨料粒径对混凝土有效弹性模量的影响

2.2 界面特性对混凝土有效弹性模量的影响

保持其他参数不变,分别设界面弹性模量与水泥浆基体弹性模量之比q=0.2,0.4,0.6,0.8和1.0,混凝土有效弹性模量分别为35.083 GPa,37.681GPa,38.726 GPa,39.303 GPa和 39.679GPa。由此可以得出:提高界面的弹性模量,可在一定程度上提高混凝土有效弹性模量,但是随着界面弹性模量的增大,有效弹性模量增大的速度越来越缓慢,毕竟界面在混凝土中占的比例很小。

再分别设界面泊松比νi=0.15,0.20,0.25,0.30和0.35,其他参数保持不变,结果如图5(a)所示,从图中可以看到,混凝土有效弹性模量变化非常小,但依然可以看出,随着界面泊松比的增大,混凝土有效弹性模量先减小再增大。由图5(b)可见,对于各级骨料体积分数,界面泊松比对混凝土有效弹性模量的影响都很小。

图5 界面泊松比对混凝土有效弹性模量的影响

分别设界面厚度h=0.2 mm,0.3mm,0.4mm,0.5mm,0.6mm,其他参数保持不变,混凝土有效弹性模量分别为34.669GPa,34.667GPa,34.605GPa,34.571GPa,34.535GPa。由此可以看出:由于界面弹性模量小于水泥浆基体的弹性模量,混凝土有效弹性模量随着界面厚度的增大而减小。而实际混凝土中界面过渡层的厚度不到0.1mm,一般认为其约为0.05mm,所以说它对混凝土有效弹性模量的影响是有限的。

2.3 缺陷对混凝土有效弹性模量的影响

取圆形孔隙孔径为1.5mm,币状裂隙长半轴长为2mm,长细比为10∶1,设圆形孔隙率分别为0,1%,2%,3%,4%和5%,币状裂隙率为0,0.6%,1.3%,1.9%,2.5%时,运用数值模型计算混凝土有效弹性模量,得到的结果如图6所示。从图6可以看出,混凝土有效弹性模量随着缺陷体积分数的增大而减小,而且币状裂隙对于混凝土有效弹性模量的减小幅度明显大于圆形孔隙。这说明缺陷的存在在一定程度上会减小混凝土的有效弹性模量,弱化它的力学性能,这也解释了为什么混凝土的强度会远低于它的理论强度。同时,币状裂隙对于混凝土有效弹性模量的影响大于圆形孔隙,这是因为币状裂隙有尖角,容易产生应力集中现象,所以它对混凝土力学性能的影响比较大。

图6 缺陷体积分数对混凝土有效弹性模量的影响

2.4 各组分弹性模量对混凝土有效弹性模量的影响

取Va=40%,分别把砂浆和骨料的弹性模量按一固定步长不断增加,此处设为0.62GPa,计算混凝土有效弹性模量,结果如图7所示,可以看出,随着砂浆弹性模量的增大,混凝土有效弹性模量也增大,而且几乎是线性关系;而其他参数不变,增大骨料的弹性模量,混凝土有效弹性模量也是增大的,且几乎是线性关系,不过两者相比,砂浆的斜率更大,所以砂浆对混凝土有效弹性模量的影响更大。

2.5 骨料形状对混凝土有效弹性模量的影响

由于前面已经计算过骨料为圆形时混凝土骨料体积分数分别为20%,40%和60%时的混凝土有效弹性模量,为了减少计算量,此处有关模型参数同第1.3.4节中。

图7 砂浆和骨料弹性模量对混凝土有效弹性模量的影响

图8是骨料为任意多边形和圆形时得出的混凝土有效弹性模量的结果与试验值的比较。从图8可以看出,骨料为任意多边形时混凝土有效弹性模量预测值更接近试验值。

图8 骨料形状对混凝土有效弹性模量的影响

3 结 论

本文主要围绕含缺陷混凝土材料的有效弹性模量预测方法进行研究,结果表明细观力学数值均匀化方法预测含缺陷混凝土的有效弹性模量是可行的,预测值与试验值吻合较好。同时表明,缺陷的存在会减小混凝土的有效弹性模量,且币状裂隙比圆形孔隙影响更为明显;随着骨料或砂浆弹性模量的增大,混凝土的有效弹性模量增大;界面特性参数和骨料最大粒径对混凝土有效弹性模量的影响有限;骨料为任意多边形时混凝土的有效弹性模量预测值更接近试验值。

:

[1]宋玉普.多种混凝土材料的本构关系和破坏准则[M].北京:中国水利水电出版社,2002:32-36.

[2]王祥林,卢东红,王力平.水泥石的动态性能研究[J].哈尔滨建筑大学学报,1995,28(5):7-11.

[3]黄克智,徐秉业.固体力学发展趋势[M].北京:北京理工大学出版社,1995:196-198.

[4]马怀发,陈厚群,黎保琨.混凝土试件细观结构的数值模拟[J].水利学报,2004,35(10):27-35.

[5]赵爱红,虞吉林.含正交排列夹杂和缺陷材料的等效弹性模量和损伤[J].力学学报,1999,31(4):475-483.

[6]MORI T,TANAKA K.Averate stress in matrix and average elastic energy of materials with misfitting inclusions[J].Acta Metal,1973,39:587-606.

[7]BUDIANSKY B.On the elastic moduli of heterogeneous material[J].J Mech Phys Solids,1965,13:223-227.

[8]JUN S,JASIUK I.Elastic modulioftwo-dimensional composites with sliding inclusions-a comparison of effective medium theories[J].Int J Solids&Structs,1993,30:2501-2523.

[9]NORRIS A N.A differential scheme for the effective moduli of composites[J].Mech of Mat,1985,4:145-151.

[10]高蕴昕,郑泉水,余寿文.损伤体有效弹性性质的细观分析和不变性描述:一个考虑微缺陷相互作用的一般理论模式[J].力学学报,1998,30(5):552-563.

[11]CHRISTENSEN R M,LO K K.Solutions for effective shear properties in three phase sphere and cylinder models[J].J Mech Phys Solids,1979,27:315-330.

[12]KCHANOV M.Elastic solids with many cracks and related problems[J].Advances in Applied Mechanics,1993,30:259-428.

[13]WANG A S D.A probabilistic-mechanic approach of damage mechanics for fiber-reinforced composites[C]//SUN C T,LOO T T.Proceedings of Second International Symposium on Composite Materialsand Structures.Beijing:Chinese Society of Theoretical and AppliedMechanics,1992:1-19.

[14]YAN Xiang-qiao.An effective numerical approach for multiple void-crack interaction[J].Journal of Applied Mechanics,2006,73:525-535.

[15]HUANG JH,LIU K K.On a flat ellipsoidal inclusionor crack in tree-dimentional anisotropic media[J].Int J Eng Sci,1998,36:143-155.

[16]CHEN Y Z.General case of multiple crack problems in an infinite plate[J].Engineer Fracture Mechanics,1984,20:591-597.

[17]应宗权,杜成斌,孙立国.基于随机骨料模型的混凝土弹性模量预测[J].水利学报,2007,38(8):933-937.

[18]应宗权,杜成斌.考虑界面影响的混凝土弹性模量的数值预测[J].工程力学,2008,25(8):92-96.

[19]杜成斌,孙立国.任意形状混凝土骨料的数值模拟及其应用[J].水利学报,2006,37(6):662-667.

[20]STOCK A F,HANNANT D J,WILLIAMS R I T.The effect of aggregate concentration upon the strength and modulus of elasticity of concrete[J].Magazine of Concrete Research,1980,32(113):225-234.

[21]WALRAVEN J C,REINHARDT H W.Theory and experiments on the mechanical behavior of cracks in plain and reinforced concrete subjectedto shear loading[J].Heron,1981,26(1A):26-35.

[22]王静薇.混凝土细微观结构与强度的关系[D].杭州:浙江大学,2006:14-19.

[23]刘冰.高强混凝土试验及破坏过程模拟[D].南京:河海大学,2006:44-48.