阻尼的非自治Sine-Gordon方程的核截面

班爱玲

（池州学院 数学计算机科学系，安徽 池州247000）

阻尼的非自治Sine-Gordon方程的核截面

班爱玲

（池州学院 数学计算机科学系，安徽 池州247000）

本文证明了具有阻尼的非自治Sine-Gordon方程所产生的过程是一致渐近紧的，进而得到该系统存在核截面。

阻尼； 过程； 核截面

1 引言

设Ω是Rn中的一个有界开子集，且边界Ω充分光滑，考虑如下非自治Sine-Gordon方程的初边值问题：

其中u=u(x,t)是Ω×[t,+∞上的实值函数，α,β是两个给定的正常数，f(x,t)∈C′(R×R,L2(Ω))

系统(1)是描述连续Josephson联结的动力学行为[1]。Sine-Gordon方程具有许多有趣的物理现象和实用价值，因而它成为无穷维动力系统中的一个重要模型。

对于方程（1）的自治情形（即f不依赖于时间t），系统（1）产生的解映射 U(t,t)=U(t-t,0)简化为一个半群或半流，许多人曾对此作出大量的研究工作，主要证明了系统（1）存在全局吸引子，并得到该全局吸引子的Hausdorff维数的上界估计[2-4]。

对于非自治波动方程系统而言，它的解定义了一个连续的过程.Chepyzhov.V和Vishik.M研究了它的核截面的存在性， 并得到该核截面的Hausdorff维数的上界估计[5-6]。最近，班爱玲、周盛凡等对此也做了一些工作，并对上述结果做了必要的改进[7]。

本文主要讨论阻尼的非自治Sine-Gordon方程的核截面的存在性。

2 预备知识

设算子A=-△:D(A)=H01(Ω)∩H2(Ω)是自伴的、正定的、线性的，A的特征值 λj｛ ｝j∈N满足：

设H是一个Banach空间，含有双参数映射族U(t,τ)｛ ｝xt≥τ≥是定义在H上的一个连续过程，即（i）对于每个τ∈R，U(t,τ)是H上的单位映射；（ii）对于所有t≥s≥R，都有U(t,s)U(t,τ)=U(t,τ)；（iii）对于所有t≥τ，τ∈R,x∈H,U(t,τ)x关于(t,τ,x)是连续的。一条曲线φ(s),s∈R，若满足，则称其为过程 U(t,τ)｛ ｝xt≥τ的一条完整的轨道。过程U(t,τ｛ ｝)t≥τ的核是有过程的所有有界轨道组成的，即是K在s时刻的截面，简称为过程 U(t,τ｛ ｝)t≥τ的核K截面。

其中u(t)是系统（1）的解，见 [2,6]中的相关定理。

3 过程的耗散性

本节中，我们将给出过程 U(t,τ｛ ｝)t≥τ在E中存

在一个有界吸收集。

设φ=(u,v)T，v=ut+εu,其中

则系统 （1）等价于下面关于时间的一阶发展方程：

其中

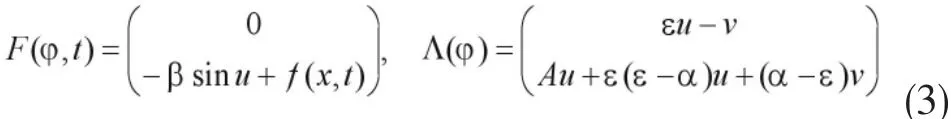
显然，系统（2）在E中也是适定的，对于每个初值φ (τ)∈E，系统（2）存在唯一的连续解φ(t)∈C((τ,+∞), E)，通过解定义一个解过程

且Uε（(t,τ)）=RεU(t,τ)R-ε，其中Rε:(a，b)T→(a,b+εa)T是E中的一个同构，因此，我们仅需考虑系统（2）。引理1 如果f∈C′([t,+∞],L2(Ω))，存在一个常数r0＞0，对于中的任意有界集B，存在T0(B)＞0，使得对于φ(τ)∈B，系统（2）的解φ(τ)=(u(t),v(t))T，满足

证明：设v=u1+εu,由系统 （1）的第一个方程得，

用v与方程（4）的两边在L2(Ω)中作内积得，

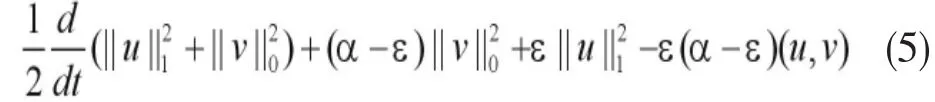
其中

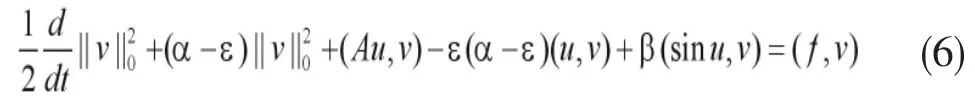
利用poincare不等式得，

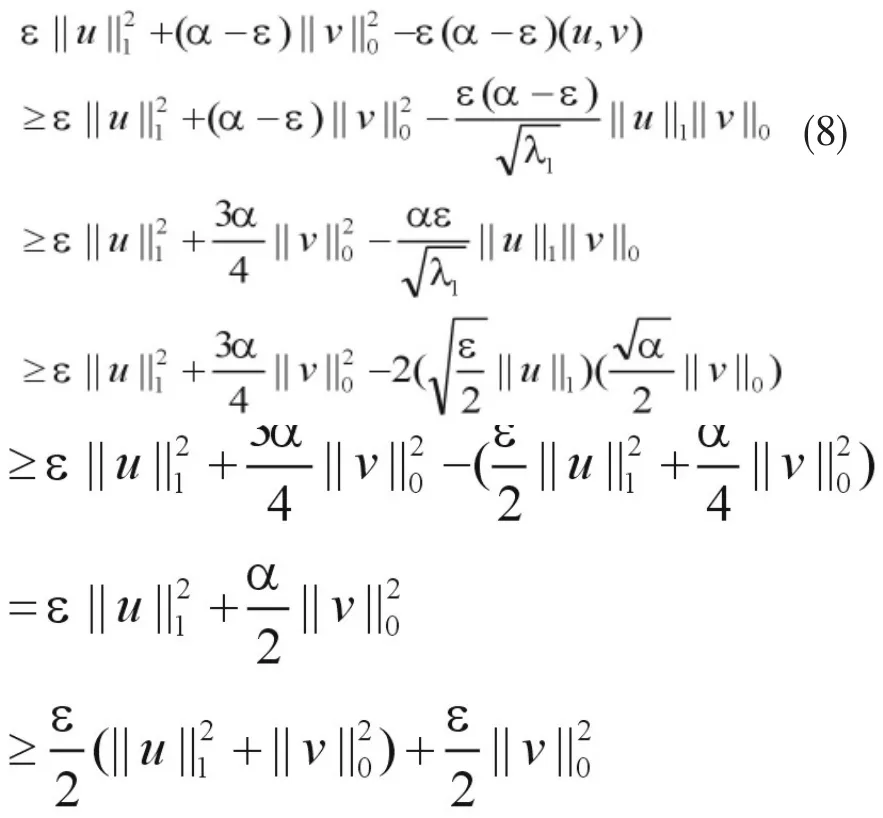
由（6）、（8）得，

即，

利用Gronwall′s不等式得，

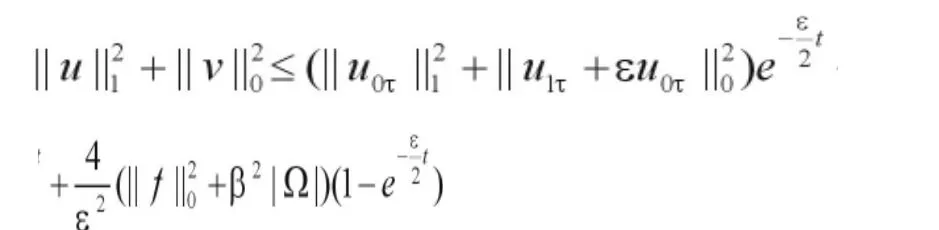
因此得到，

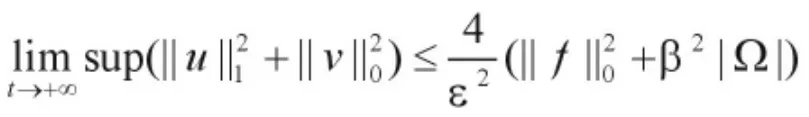
（不依赖于τ），

证毕

引理2 过程 Uε(t,τ｛ ｝)t≥τ在E中是耗散的，且所有的有界集轨道都是有界的。

证明：由引理1的结果得知。

4 存在紧的核截面

为了证明过程 Uε(t,τ｛ ｝)t≥τ存在非空的紧的核截面，我们需要证明过程 Uε(t,τ｛ ｝)t≥τ在中存在一致（关于τ∈R）渐近紧的吸引集。

引理3 如果函数f∈C′[τ，+∞，L2（Ω）那么系统（2）在中产生的过程 Uε(t,τ｛ ｝)t≥τ具有一个一致 （τ∈R）紧的吸引集即过程 Uε(t,τ｛ ｝)t≥τ在中是一致（τ∈R）渐近紧的。

证明：设φ(t)是系统（2）带有初值φ(t)∈B0的解，将φ(t)分成两个部分：

其中φ1和φ2分别满足：

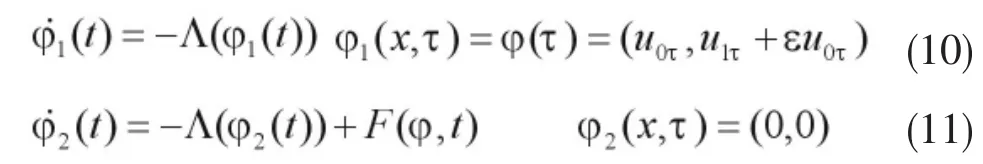
由（10），可推导出

因此有，

即，（10）的解随着时间的增加成指数衰减的。

下面将要证明（11）的解在空间中是有界的。

由（11）得，

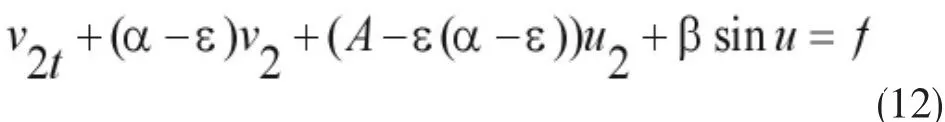
用Av2与方程（12）的两边在L2(Ω)中作内积得，

类似于前面第三节中（8）的证明，得，

同时，

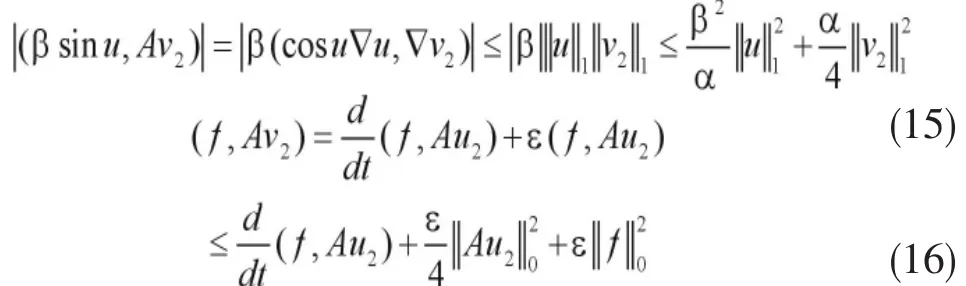
由（13）-（16）得，

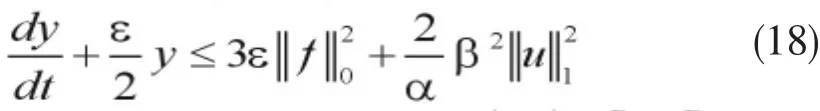
由（18）得，

设B1是E1中以（A-1f，0）为球心，半径为r的有界闭球，因此，B1是过程 Uε(t,τ｛ ｝)t≥τ的一致 （关于τ∈R）紧的吸引集，即对于任意的，使得

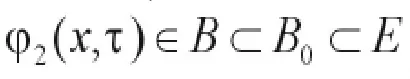
也即，过程 Uε(t,τ｛ ｝)t≥τ是一致（关于τ∈R）渐近紧的。

定理 如果函数f∈C′[τ，+∞，L2（Ω），那么系统（2）在中所产生的过程 Uε(t,τ｛ ｝)t≥τ存在一个非空的核K，且核的每个核截面都是紧的。证明：直接由引理3的结果得到。

[1]X.M.Fan.Random attractor for a damed Sine-Gordon equation with white noise[J].Pacific J.Math.,2007,19(1):63-76.

[2]Temam.R.Infinite-dimensional Dynamical Systema in Mechanics and Physics[M].2nd Edition.Appl.Math.Sciences 68,New York:Springer-Verlag,1997.

[3]J.M.Ghidaglia and R.Temam,Attractor for damped nonlinear hyperbolic equations[J].J.Math.Pures Appl.,1987,66:273-319.

[4]周盛凡.有阻尼Sine-Gordon方程的全局吸引子的维数[J].数学学报，1996,39(5):597-601.

[5]Chepyzhov.V and Vishik.M.A Hausdorff dimension equations estimate for kernel sections of non-autonomous evolution[J]. Iniana Univ.Math.J.,1991,140:193-206.

[6]Chepyzhov.V and Vishik.M.Attractor for equations of mathematical physics[M].AMs,Providence,RI,2002.

[7]A.L.Ban,S.F.Zhou,X.Y.Han.Dimension of kernel sections for damped non-autonomous wave equation with critical exponent[J].J.Math.Phys.,2009,50:1-9.

[责任编辑：曹怀火]

0175

A

1674-1102（2010）03-0007-03

2010-04-13

班爱玲（1982-），女，安徽巢湖人，池州学院数学计算机系教师，硕士，研究方向为微分方程与动力系统。