巧用惯性力

高炳坤

(清华大学物理系,北京 100084)

巧用惯性力

高炳坤

(清华大学物理系,北京 100084)

利用惯性力,巧妙地破解了两个疑案.

引力;惯性力

如图1所示:从地面上看,质量为 m的小球于零时刻在离地面h1处由静止自由下落,于 t时刻落到离地面h2处,其速度为 v.小球的动量的增量为

其动力学原因是小球受到了地球的引力 mg,由质点的动量原理知

今选“小球与地球”为一系统,仍从地面上看,则系统的初动量为(设地球质量为 Me)

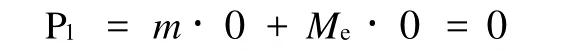
系统的末动量为

所以系统的动量的增量为

式(3)与式(1)相同,这清楚地表明:“小球与地球”这个系统的动量改变了.由系统的动量原理知,“小球与地球”这个系统的动量变化等于外力的冲量.这外力是什么呢?!

图 1

图 2

暂将“疑案”悬起,再看图2又生“疑案”.图2中小球相对于地面的运动情况与图1完全相同.选“小球与地球”为系统,从地面上看,人所共知系统的机械能守恒,即

图2中有一以恒速 u运动的电梯,从电梯上看“小球与地球”系统,其机械能是否仍守恒呢?让我们拭目以待:系统的初机械能为

系统的末机械能为

所以系统的机械能的增量为

将式(4)代入上式得

式(5)清楚地表明,从电梯上看“小球与地球”这个系统的机械能竟然不守恒了,原因何在?!

两大疑案(式(3)与式(5))令人瞠目.作者经多年思考,终于悟出了两大疑案同出一源,下面破解之.如图3所示:地球对小球的引力为 mg,则小球对地球的反作用力为-mg,其作用点为地心 C.选“小球与地球”为系统时,mg与-mg是系统的内力.但对地球而言-mg却是外力,它使地球相对于惯性系产生的加速度为

图 3

这个a也是匀速运动的电梯相对于惯性系的加速度.这个加速度尽管很小,但它从“质上”断定了地面与匀速运动的电梯不是惯性系.因此,在此二非惯性系中小球与地球必分别受惯性力

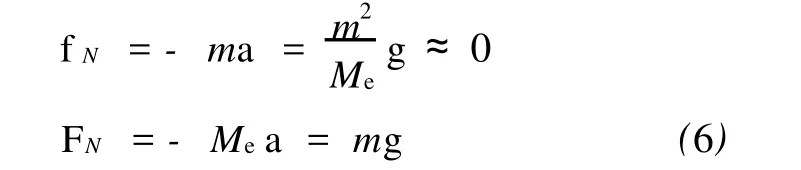
fN固然微不足道,但 FN却大到了与系统的内力mg相等的地步,决不可忽视,而且正是 FN揭开了两个疑案的谜底.如图4所示,选“小球与地球”为系统时,则 mg与-mg为内力,FN为外力;内力不影响系统的动量,外力 FN正是系统的动量变化的原因,下面定量分析之.FN的冲量为

将式(7)与式(2)、式(3)比较知

式(8)表明:在非惯性系中,“包含惯性力的冲量的动量原理”是成立的.这就破解了第一个疑案.

下面来破解第二个疑案.从电梯上看,FN的作用点C以-u移动,故 FN必做功

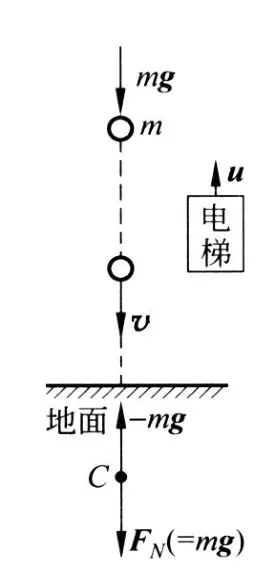
图 4

将式(9)与式(2)、式(5)比较知

式(10)表明:在非惯性系中,“包含惯性力的功的功能原理”是成立的.这就破解了第二个疑案.地球所受的惯性力 FN,不仅破解了上述两个疑案,而且还使其他问题迎刃而解,例如:①从地面上看,为何“小球与地球”系统的机械能守恒呢?那是因为 FN的作用点C不移动,FN不做功;②为何教科书中常把地面称作惯性系呢?那是因为教科书中研究的是其他物体相对于地面的运动,而FN并未作用在其他物体上.

[1] 高炳坤,谢铁曾.地球所受的一种易被忽视的惯性力[J].大学物理,1991,(11)

[2] 高炳坤.力学中一个令人费解的问题[J].大学物理,1995,(5)

[3] 高炳坤.能量追踪[J].大学物理,2001,(3)

2010-07-26)