底栖生物生物量空间插值方法研究
2010-09-05张伟李纯厚贾晓平陈丕茂方良
张伟,李纯厚,贾晓平,陈丕茂,方良
(中国水产科学研究院南海水产研究所、农业部海水养殖生态与质量控制重点开放实验室、农业部南海渔业资源重点野外科学观测试验站,广东 广州 510300)
底栖生物生物量空间插值方法研究
张伟,李纯厚,贾晓平,陈丕茂,方良
(中国水产科学研究院南海水产研究所、农业部海水养殖生态与质量控制重点开放实验室、农业部南海渔业资源重点野外科学观测试验站,广东 广州 510300)
在地统计学和地理信息系统支持下,采用反距离加权(Inverse distance weighting,IDW)、径向基函数(Radial basis functions,RBF)、普通克里格 (Ordinary Kriging,OK) 3种插值方法对2007年4月获得的大亚湾人工鱼礁区及附近海域底栖生物生物量数据进行空间插值方法研究,并对插值精确度进行交叉验证。结果显示,经对数转化后的数据呈正态分布,而且3种插值方法对其进行插值,所得的等值面图效果比原始数据所得等值面图效果好。交叉验证显示,对数转化数据插值精确度OK>RBF>IDW。观察插值结果等值面图,发现3种方法均能较客观地模拟出底栖生物生物量的总体分布趋势,在对局部趋势的模拟上,OK的表现效果最好。
底栖生物生物量;空间插值;研究
底栖生物是水生态系统的重要组成部分,是海洋中各种鱼类生长和繁殖的饵料基础,是海洋生态动力学研究的重要对象[1]。因此研究水域中底栖生物的资源状况,对于深入探讨水域生态环境、水生生物区系、群落组成和鱼类资源变化都有重要的科学价值和实际意义。
地理信息系统(GIS)具有很好的空间数据处理和分析功能,如它提供的地统计方法就是一种全新的解决问题的方案,空间插值是其重要的功能之一。ArcGIS地统计分析模块在地统计学与GIS之间架起了一座桥梁。使得复杂的地统计方法可以在软件中轻易实现。体现了以人为本、可视化发展的趋势。
空间插值法可以用已知的空间数据估计(预测)未知空间的数据值[2],它已经用于很多领域的研究中,如:气象[3,4]、降雨[5,6]、土壤[7]等。这些领域都进行了空间插值的比较研究,但是对于海洋底栖生物的研究还鲜有报道。因此,本文进行了初步的尝试,利用2007年4月在大亚湾所设的12个站点的底栖生物生物量数据资料进行空间插值方法研究,探讨不同种类插值方法的应用效果,以为今后底栖生物插值方法的应用起到一定的参考作用。
1 材料与方法
1.1 数据来源
采用2007年4月,在深圳杨梅坑人工鱼礁区及附近海域(22°32.94′—22°34.98′N,114°34.48′—114°36.57′E),设12个站位进行底栖生物调查。调查站位设置见图1。底栖生物的采集和分析均按《海洋监测规范》[8](GB17378-1998)和《海洋调查规范—海洋生物调查》[9](GB12763.6-91)中规定的方法进行。本文采用底栖生物生物量数据进行空间插值方法研究。
1.2 GIS软件与统计软件
软件采用美国环境系统研究所 (ERSI) 的GIS桌面平台系统ARCGIS 9.2,选用SPSS13.0以及EXCEL 2003作为数据统计分析的工具。利用地理信息系统软件ARC/INFO 9.2的空间分析模块(Spatial Analyse) 和地理统计模块 (Geostatistical Analyst)[10,11]提供的3种插值方法:反距离加权法、径向基函数法和普通克里格法。
1.3 探索性空间数据分析和数据转化
1.3.1 数据分布检测 数据检测,即空间数据探索分析(ESDA)。ARC/INFO 9.2提供了多种检测数据分布特征的方法。对于正态分布,有一个快速检验的方法:如果平均值与中值大致相等,就可以把它当作数据服从正态分布的证据之一。另一种检验方法是正态QQ图,检查数据的正态分布情况。其作图原理是用分位图思想,直线表示正态分布,如果数据接近一条直线,则它们越接近于服从正态分布。
1.3.2 数据转化 很多插值和统计分析方法要求数据符合正态分布[11]。根据探索性空间数据分析得到的数据性质,选择合适的转化方法,可使数据基本上符合正态分布。通过分析,得出对原始数据进行对数转化,可使转化后的数据呈正态分布。
1.4 空间插值方法
目前,用于海洋底栖生物的空间插值方面的研究鲜见报道,本研究主要采用反距离加权插值法、径向基函数插值法和普通克里格3种方法。
1.4.1 反距离加权法 反距离加权(inverse distance weighted,IDW)插值法基于相似原理,即两个物体离得越近,它们的性质就越相似;反之,离得越远则相似性越小。它是最常用的空间内插方法之一,

图1 大亚湾底栖生物调查站位示意图Fig. 1 Sampling stations of Macrobenthic in the Daya Bay
式中:Z为估计值,Z为第i (i=1,…,n)个样本,Di为距离,P为距离的幂,其显著影响内插的结果,它的选择标准是最小平均绝对误差。
这种空间插值方法的优越性是直观并且效率高,在已知点分布均匀的情况下插值效果好。
1.4.2 径向基函数插值法 径向基函数法是人工神经网络方法中的一种。由径向基函数生成的表面不仅能够反映整体变化趋势,而且可以反映局部变化。当取样点拟合的曲面不能准确地代表表面时,可以采用径向基函数法。
1.4.3 克里格插值法 克里格(Kriging)插值法是空间统计分析方法的重要内容之一,它是建立在半变异函数理论分析基础上的,是对有限区域内的区域化变量取值进行无偏最优估计的一种方法。Matheron[12]给出了克里格法的一般公式:

即

选取iλ,使的估计无偏,并且使方差2iσ小于任意观测值线形组合的方差。
克里格方法进行插值时,不仅考虑了待预测点与邻近点数据的空间距离关系,还考虑了各参与预测的样点之间的位置关系,充分利用了各样点数据的空间分布结构特征,使其估计结果比传统方法更精确,更符合实际,更有效地避免了系统误差的出现。
1.5 验证方法
采用交叉验证法 (cross validation) 来验证插值的效果。对于每一种插值法,交叉验证分析重复从已知数据集中删除一个采样点的过程,用剩下的采样点估算被删除点的数值,并计算误差均值(MEAN) 和误差均方根 (Root-Mean-Square,RMS)。一般来说,各种插值方法的误差均值绝对值和误差均方根总体最小者,具有较好的插值效果,尤其是RMS越小越好[13]。
2 结果分析
2.1 数据分布
人工鱼礁区12个站位底栖生物生物量的平均值为48.05g/m2,中值为21.45 g/m2,两者差别比较大,不属于正态分布;正态QQ图上,12个站位生物量基本上不在一条直线上,因此,也不属于正态分布。
上述两种方法所得出的结果都表明12个站位底栖生物生物量都不接近正态分布。因此,对其分析时,要进行数据转化。
2.2 数据转化
对数据变换会使数据更趋于正态分布并且会提高预测的精度[14,15]。很多学者运用对数、立方根、平方根等变换方式对数据进行预处理以提高插值的精度。研究中我们在对样本数据进行分析的基础上对其进行了变换方式的优化选择,结果表明:经过对数转换后的数据从整体上更趋向于正态分布,原始数据和对数转化后数据的正态分布见图2所示。因此,在整个分析过程中,对底栖生物我们均采用了原始数据与对数变换两套数据,并对其插值结果进行了对比分析。
2.3 插值结果与分析
插值方法的比较分析采用了反距离权重法、径向基函数和普通克里格法。反距离权重法的距离权重指数为2,站点搜索范围为临近的12个站点;径向基函数,站点搜索范围为临近的12个站点;克里格法的半方差函数分两种情况:原始数据采用圆形模型(#KRIGING_CIRCULAR),而对数转化数据采用高斯模型(#KRIGING_GAUSSIAN),站点搜索范围也为临近的12个站点;各种插值方法在检验站点的结果误差如表1。
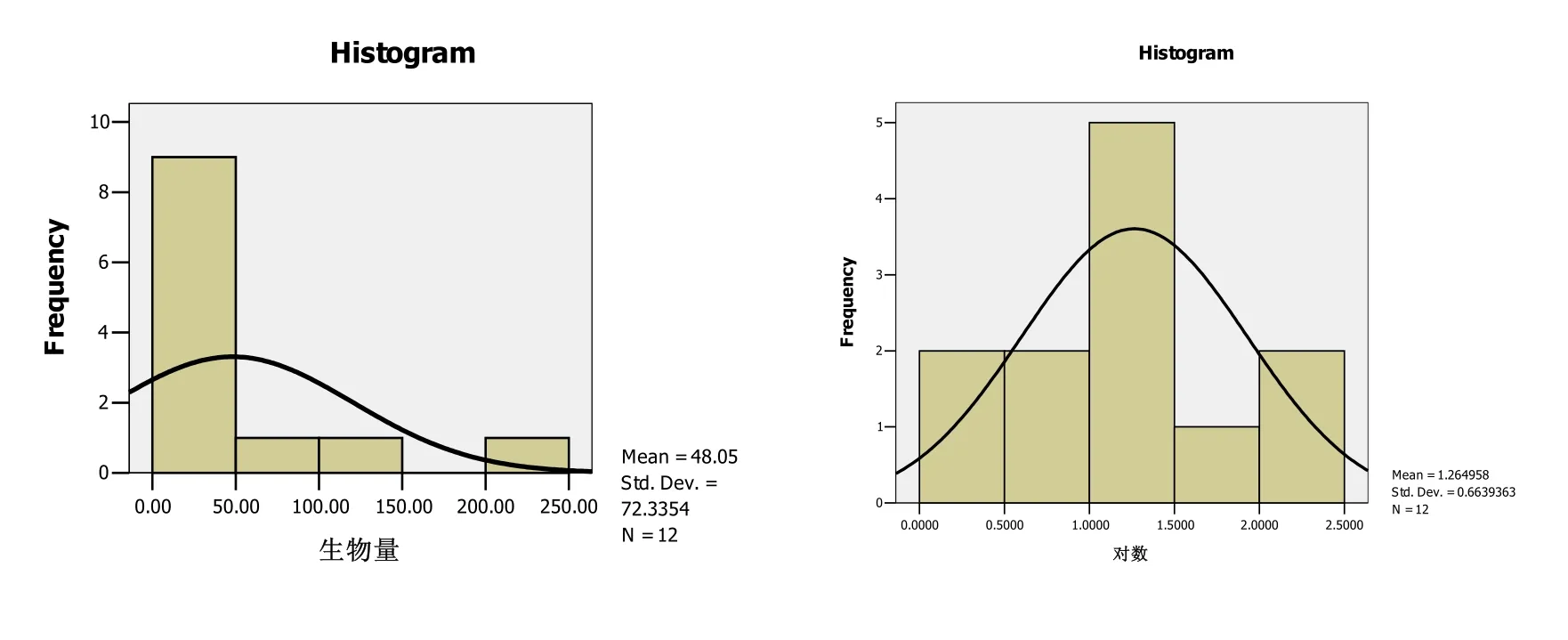
图2 底栖生物生物量原始数据和对数转化数据分布图Fig. 2 Distribution map of raw and log-transformed data of Macrobenthic biomass
2.3.1 数据转化对插值结果的影响
表1表明,在数据转化后,3种方法的MEAN和RMS绝对值均有所下降,充分显示出数据经过转化后,精度明显上升,而且上升幅度比较大。通过采用3种方法比较发现,使用原始数据进行插值分析时,IDW和RBF的插值效果均比OK 的插值效果好。而经过对数转化以后,对其进行插值分析,OK的插值效果比IDW和RBF的插值效果好。同时,从插值结果等值面图来看(图3),转化基本消除了由于极大、极小值引起的小等值线圈、尖锐的等值线锯齿、缺刻等插值噪音,使底栖生物生物量的平面分布趋势更明晰易辨。

表1 不同插值方法得到的误差均值和误差均方根Tab. 1 MEAN and RMS calculated by different interpolation methods
2.3.2 不同插值方法比较 以转化后数据的插值结果作为不同方法比较的依据。
由表1可见,3种方法得到的误差均值绝对值和误差均方根的大小顺序均为OK<RBF<IDW,说明3种方法对大亚湾底栖生物生物量数据的插值精确度,OK最高,RBF次之,IDW最低。然而,通过RMS比较,发现两种方法得出的结果都具有较高的精度,仅 IDW和RBF略逊于OK。这是因为OK法在插值过程中充分利用了数据点之间的空间相关性。但从整个插值计算过程来看,IDW和RBF比OK要相对简单。表明此3方法在底栖生物插值模型中均能获得较好效果。
一方面,从整体上观察使用3种方法得到的空间插值图(图3),底栖生物分布的基本趋势是一致的,都是附近海域的平均生物量最高,平均生物量最低为在建礁区。因此,可以说这3种插值方法都基本上表明底栖生物的空间分布趋势。
另一方面,从较小的空间尺度观察插值平面(图3),发现IDW生成的等值线往往会围绕生物量值极大或极小的采样点发生大曲率的弯曲,甚至闭合形成小等值线圈,说明IDW对极端值敏感,这会对整体趋势产生干扰。RBF适用于对大量点数据进行插值计算从而获得平滑表面,这样能够很好的反映整体变化趋势。但是忽略了对较小空间尺度变化趋势的表现。只有OK,既具有高耐抗性,又能在等值线的平滑度与精确度之间达到较好的平衡,对总体趋势与局部趋势都有良好的表现。
综上所述,以上3种插值方法,都能很好的模拟出底栖生物的分布趋势,而从较小的空间尺度看,结合交叉验证的结果,OK的插值效果是最好的,是最适合用于底栖生物生物量数据的插值方法。
3 讨 论
影响底栖生物空间插值精度的因素主要有2个,一个是插值方法本身引起的误差,如在插值过程中插值方法的选择、各参数的选取等。另一个是外界因素对底栖生物的影响而引起的误差,如经纬度、离岸距离、沉积环境、人为扰动、频繁渔业、底栖生物站点的数目和分布状况、观测数据本身的误差等。
空间内插是地学中尤其是资源、环境和生态研究中极为重要的一种空间分析方法。空间内插是研究区域变量空间分布的基本方法,应该充分利用空间插值技术获取更多精确数据,尤其是对于站点稀少,而站点分布又不合理的地区。同时,选择合适的插值方法也要结合数据本身的特点和空间特性,并不是越复杂的方法就一定能产生越好的估值效果。各种方法都有其特定假设、适用范围、算法和优缺点,对于众多的空间内插方法而言,没有绝对最优的空间内插方法,只有特定条件下的最优方法。
对深圳杨梅坑人工鱼礁区及附近海域底栖生物而言,3种插值方法中,IDW和RBF的插值效果基本一致,而OK的插值效果是最好的,这一研究结果与林琳[16]等的研究结果基本一致。但是IDW和RBF操作起来比较简单,而OK则需要耗费大量的时间在分析原始数据和半变异函数的训算和理论模型的拟合建立上,而且其数学过程相对复杂,运算耗时也长。在研究目的许可的情况下,简单、灵活的IDW、RBF也是合适的选择。如果需要利用插值结果进行更精细,更高级的空间分析,如图形叠加、构建生态系统模型等,则必须选择插值精度最高、对小空间尺度表现最好的插值方法,因为误差会发生上行传递和放大,造成更深远的影响[17]。

图3 大亚湾底栖生物生物量的插值结果等值面图Fig. 3 Interpolation result of the Macrobenthic Biomass in the Daya Bay
底栖生物空间插值中应关注站点数量、分布状况以及适合数据本身特点的插值方法。时空尺度带来的不确定性都可归结为站点数量能否充分反映底栖生物的时空变异特征,所以增加站点数量是提高插值精度的关键之一,而插值方法的选择以及参数的设置也要根据具体的数据情况进行详细的分析,从而使插值得到最好的效果。
该文初步尝试应用底栖生物生物量数据进行了3种插值方法应用效果的对比分析,得出OK的插值效果是最好的,是最适合用于底栖生物生物量数据的插值方法。为今后底栖生物的研究提供了一种方法学的指导,然而,空间插值方法在底栖生物中的应用还处于起步阶段,还需要做更深入的研究。
[1] 唐启升. 中国海洋生态系统动力学研究. 北京: 科学出版社,2000.
[2] 李新, 程国栋, 卢玲, 等. 空间插值方法比较 [J]. 地理科学进展,2000, 15(3): 260-265.
[3] 李军龙, 张剑, 张丛, 等. 气象要素空间插值方法的比较分析[J]. 草业科学, 2006, 23(8): 6-11.
[4] 封志明, 杨艳昭, 丁晓强, 等. 气象要素空间插值方法优化 [J].地理研究, 2004, 23(3): 357-364.
[5] 刘胤雯, 赖格英, 陈元增, 等. 梅江河流域年均降雨量空间插值方法研究 [J]. 亚热带资源与环境学报, 2007, 2(3): 30-34.
[6] 朱会义, 贾绍凤. 降雨信息空间插值的不确定性分析 [J]. 地理科学进展, 2004, 23(2): 34-42.
[7] 王秀, 苗孝可, 孟志军, 等. 插值方法对GIS土壤养分插值结果的影响 [J]. 土壤通报, 2005, 36(6): 826-830.
[8] 国家海洋局. 海洋监测规范. 北京: 海洋出版社, 1991.
[9] 国家海洋局. 海洋调查规范. 北京: 海洋出版社, 1975.
[10] JILL M, KEVIN J. Using ArcGIS Spatial Analyst. CA USA,Redlands, 2001:136-148.
[11] KEVIN J, JAY M H, KONSTANTIN K, et al. Using ArcGIS Geostatistical Anaslyst. CA USA, Redlands, 2001:116-162.
[12] MATHERON G. Principles of geostatistics [J]. Economic Geology,1963, 58: 1246-1266.
[13] 孟庆香, 刘国彬, 杨勤科. 黄土高原降水量的空间插值方法研究[J]. 西北农林科技大学学报(自然科学版), 2006, 34(3): 83-88.
[14] Michael F Hutehinson. Interpolation of rainfall data with thin plate smoothing splines-Part I: two dimensional smoothing of data with short range correlation [J]. Journal of Geographie Information and Decision Analysis, 1998, 2(2): 139-151.
[15] Mare G, Genton. Analysis of rainfall data by robust spatial statistic using s+sPATIALsTATs [J]. Journal of Geographic Information and Decision Analysis, 1998, 2(2): 116-126.
[16] 林琳, 李纯厚, 戴 明, 等. 海洋浮游植物丰度的空间插值优化[J]. 生态学报, 2007, 27(7): 2 880-2 888.
[17] Mitas L, Mitasova H. Spatial interpolation methods in GIS. In:Longley P A ed. Geographical information system. volume 1,principles and technical issues, second edition. New Y0rk: Join Wiley & Sons, 1999: 452-461.
Research on spatial interpolation methods of Macrobenthic biomass
ZHANG Wei, LI Chun-hou, JIA Xiao-ping, CHEN Pei-mao, FANG Liang
(South China Sea Fisheries Research Institute; Key Laboratory of Magriculture Ecology and Quality Control, Ministry of Agriculture;Key Field Scientific Experimental Station of South Sea Fishery Resource and Environment, Ministry of Agriculture, Guangzhou 510300, China)
Based on the geostatistical method and GIS, three different methods of spatial interpolation were compared:inverse distance weighting (IDW), radial basis functions (RBF) and Ordinary Kriging (OK), using the recorded Macrobenthic biomass in the artificial reef and nearby sea area of the Daya Bay, China, in April 2007. At the same time,the definition of interpolation was verified by cross-validation. The results showed that after data log-transformed assumed normal distribution, and three kinds of interpolation methods for their interpolation, from the equivalent effect of interpolation surfaces than the raw data by the equivalent effect of contours a good map. The accuracy of the OK was the highest, followed by the RBF, and then the IDW. The interpolation surfaces revealed that all of the three methods correctly showed general trends of the Macrobenthic biomass by using a series of optimization techniques.The generated by the OK were considered the best, as the method could represent both general and local trends accurately.
Macrobenthic biomass;spatial interpolation;research
Q-332; Q178.535
A
1001-6932(2010)03-0351-06
2009-05-27;
2009-07-02
国家863计划项目(2006AA100303);科技部科研院所社会公益研究专项资金项目(2005DIB3J020);公益性科研院所基本科研业务费专项资金项目(2007ZD003)
张伟 (1982-),女,天津市,硕士,研究方向为渔业环境及其调控。电子邮箱: zhangwei_2004010@163.com
