用数学实验思想指导经济类专业《线性代数》课程的教学
2010-09-05唐耀平
唐耀平
(湖南科技学院数学与计算科学系,湖南 永州 425100)
用数学实验思想指导经济类专业《线性代数》课程的教学
唐耀平
(湖南科技学院数学与计算科学系,湖南 永州 425100)
提出了应用数学实验思想改进经济类专业线性代数教学的几点建议,即应用数学实验思想,优化教学内容;增加数学实验内容,体现学习的创造性;利用数学软件,提高学生计算能力.
数学实验;线性代数;MATLAB
《线性代数》是经济类本科专业的一门重要基础必修课。作为一个数学工具,线性代数在经济科学中有着广泛的应用。著名的投入产出模型就是以线性代数理论为基础的。学好这一门课程不仅对经济类专业课程是必不可少的,而且对掌握现代经济理论并应用于实际也是很有必要的,尤其是在计算机日益普及和广泛应用的今天,该课程的地位与作用更显重要。然而由于《线性代数》课程本身的抽象性,使得许多经济类本科生在学习该门课程时觉得难而不感兴趣,因而学不好。“数学实验”是近年来高等数学教学中用到的新的教学方法,随着计算机的发展及各种数学软件的涌现,为在线性代数课程教学中增加数学实验奠定了必要的基础。将数学实验引入线性代数课程的教学,不仅能提高学生的学习兴趣,而且可以提高学生学习数学知识和应用数学知识解决实际问题的能力。
一、用数学实验思想,优化教学内容
“数学实验”就是从问题出发,借助计算机,通过学习者亲自设计与动手操作,学习、探索和发现数学规律或运用现有的数学知识分析和解决实际问题的过程。换言之,数学实验就是学习者自主探索数学知识及其实际应用的实践过程。数学实验的目的,就是在数学的学习过程中,通过数学实验改善学生的学习方式和学习过程,从而帮助学生在自主探索和合作交流的过程中理解和掌握基本的数学知识与技能、数学思想和方法,并获得广泛的数学活动经验,有效提高数学学习的能力。
在常规的线性代数教学中,教师在课堂上首先提出问题,然后引入新的知识和方法,最后解决问题,整个过程学生是在被动地接受知识。而当代构建主义教学观认为,应将问题提出作为教学活动的一部分。全美数学教师委员会(NCTM,1991)指出:我们的数学教学应该给学生提供这样的机会——从给定情境中提出问题,或通过修改已知问题的条件去产生新的问题。数学实验是从给定情境中提出问题的最好的方法之一。经济学为线性代数的教学提供了大量的情境,比如:复杂数据的处理、银行复利的计算、状态的转移等等。通过数学实验可以帮助学生建立抽象数学和可视化的联系,实际上先做可视化模拟,再建立抽象理论已经是科学研究的一种重要途径。
例如,关于线性方程组解的情况的讨论,常规教学是通过对线性方程组的系数矩阵秩的讨论来确定的,这对经济类的本科生来说是比较抽象的。如果通过数学软件给出线性方程组的空间图形,学生就有了一个直观的理解。
这三个方程的几何意义为空间的三个平面,两两消去z,意味着求两者的交线,得到的两个二元一次方程,对应于求得的两根交线。最后由这两根交线得到的交点,该交点就是方程的解(见图 1)。当两个平面平行,没有交线,或者两根交线平行,没有交点时,方程组就不相容,因而无解;同样也可能有无穷个解。
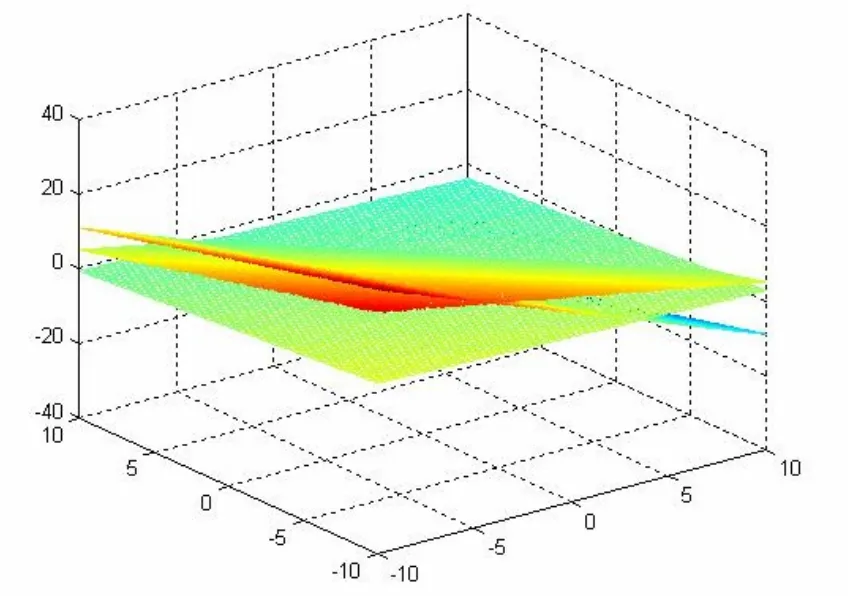
图1
利用数学软件给出抽象概念的直观理解和提高线性代数问题的数值计算应是在经管类专业学生线性代数教学中体现的数学实验思想。
二、增加数学实验内容,体现学习的创造性
目前经管类线性代数的教学大部分是采用先讲概念、性质,然后举例,最后让学生做练习,其中刻意忽略掉抽象概念的理解和定理的证明。学生在整个学的过程中是被动的接受,学的效果不好。当代的数学教学应该以“再创造”的方式来进行,让学生根据自己的体验,用自己的思维方式重新创造有关的数学知识,而不仅仅是学会教师讲授的知识。荷兰数学教育家费赖登塔尔早就指出,数学教学的核心是学生的“再创造”。
波利亚在《数学与猜想》第一卷的序言中也指出:“数学被人看作是一门论证的科学,然而这仅仅是它的一个方面。…数学的创造过程是与任何其他知识的创造过程是一样的,在证明一个数学定理之前,你先得猜测定理的内容,…你先得把观察到的结果加以综合然后加以类比。你得一次又一次的尝试。只要数学的学习过程稍微能反映出数学的发明过程的话,那么就应当让猜想、合情推理占有适当的位置”。而应用现行的线性代数的教学不需要学生进行实验、观察和猜测,学生是通过教师的“教”而掌握线性代数这一数学工具的,他们认为线性代数就是数学,为什么要学,怎么学,怎么用都不知道。而其实线性代数作为一个将复杂多元方程简单化求解的数学工具,对分析多种变量相互影响而产生复杂经济现象的经济学的贡献可谓是不言而喻的。比如欲预测10年后某地区的房屋价格,可通过搜集人均收入、土地价格、建筑原材料价格等多种变量的基期数据,用假定和计量的方法、统计学的知识分析房屋价格与各因素的相关程度并用线性代数的数学方法解多元线性方程组,从而计算出相应公式,再加入通货膨胀、利息率等现实因素,便可大致模拟出10年后该地的房屋价格。然而这些来源和背景在教学中往往被掩盖了。
实际上,线性代数的教学内容中有很多经济问题的数学模型的应用,将这些数学模型用数学实验的方法来进行求解与验证,其整个过程就是学生自主学习的创造性过程。例如经济学诺贝尔奖金获得者Leontiff获奖的工作——投入产出模型和价格均衡模型就是很好的线性代数的应用。在教学中可给出简单的例子,让学生自己建立数学模型,然后利用MATLAB软件进行求解,通过观察分析计算结果,上升为一般的理论并与Leontiff的模型进行对比,其过程就充分地体现了学生的创造性。这样的数学实验的锻炼对学生的创造性的培养是非常有效的。
三、利用数学软件,提高学生计算能力
在线性代数的学习过程中,要求学生掌握一些基本的线性代数计算问题。例如:行列式的计算,矩阵的运算,求极大无关组,解线性方程组,求矩阵的特征值、特征向量,把二次型化为标准形等等。同时还有一些高阶的线性代数问题需要准确地进行大量数据的数值计算。学生在学习线性代数时普遍感觉很抽象、很难,与微积分相比线性代数问题的计算十分繁琐,尤其在解决高于三阶的问题时其计算量是相当大的。随着个人计算机的迅速普及,各种计算软件的开发使用,使得数值计算问题的计算能力大大提高,为线性代数的教学实践带来了巨大的推动。
目前流行较广的数值计算软件是美国的 MATLAB,它是Matrix LAB(矩阵实验室)的缩写,可见开发它的初衷就是为了线性代数。所以,在线性代数教学实验中一般采用MATLAB为实验平台。学习用数学软件MATLAB解线性代数中的计算问题,过于繁杂的计算用计算机计算比用笔计算快得多。例如:求一个高阶矩阵的逆矩阵,用计算机计算只要输入一句命令就解决了,而用笔计算就比较麻烦。所以利用MATLAB进行线性代数问题的求解有三大好处:
1、提高了学生学习兴趣,加强了学生利用计算机软件解决数学问题能力的锻炼。
2、对于低阶(三阶及以下)的线性代数问题,能提供图形帮助,这对于理解线性代数的理论和概念是很有利的。
3、对于高阶的线性代数问题,通过调用函数或编程,帮助学生快速而准确地进行大量数据的数值计算。
[1]向雪萍、吴筠、王玉娟,《线性代数》实验化教学初探[J].九江学院学报,2008,(3):116-118.
[2]高淑萍,线性代数课程MATLAB实验内容的教学与研究[J].中国电子教育,2007,(4):59-62.
[3]陈怀琛、龚杰民,线性代数实践及MATLAB入门[M].北京:电子工业出版社,2005,(10).
[4]G.波利亚,数学与猜想:数学中的归纳和类比(第一卷)[M].北京:科学出版社,2003,(6).
(责任编校:何俊华)
G642.423
A
1673-2219(2010)08-0001-02
2010-05-10
湖南省教育厅教改课题(湘教通[2009]321)
唐耀平(1973-),男,湖南永州人,副教授,硕士,主要从事数学模型及矩阵反问题研究。
