边坡地震响应的动力有限元分析

李 磊，任光明，曹文广，张八二

（1．成都理工大学地质灾害防治与地质环境保护国家重点实验室，成都 610059；2．中国水电顾问集团西北勘测设计研究院兰州 730050；3．西南交通大学土木工程学院，成都 610037）

边坡地震响应的动力有限元分析

李 磊1，任光明1，曹文广2，张八二3

（1．成都理工大学地质灾害防治与地质环境保护国家重点实验室，成都 610059；2．中国水电顾问集团西北勘测设计研究院兰州 730050；3．西南交通大学土木工程学院，成都 610037）

边坡的地震响应是一个复杂的命题，也是近年来的的热点，尤其是“5．12”地震以后。目前，动力有限元是解决边坡地震响应问题行之有效的方法之一，它以地震时程加速度作为反映地震荷载的主要因素，能够定量地反映出地震时程加速对边坡不同的应力场、位移场、运动速度的影响。以某水电站坝前一个受“5．12”地震所诱发复活的巨型滑坡为例，运用动力有限元软件，对该滑坡进行了地震荷载作用下的响应分析，计算得出了地震作用下该滑坡产生的水平垂直动位移、加速度、最大剪应力场。最后，图示说明了滑坡在地震作用下的往复振动对其稳定性的影响，得到了该滑坡的安全系数时程曲线，各项计算结果量值与地震后滑坡实际量值一致，这表明“5．12”地震是导致该古滑坡复活的直接原因。

地震荷载；动力有限元；滑坡复活

1 概 述

边坡的动力问题远比静力问题复杂，目前未得到足够深度的研究，这与它涉及的学科领域繁多有关，其中包括：岩土力学、工程地质学、地震学、振动学、地球物理学、结构动力学、地震工程学等，且岩土体动力学的研究更晚，尤其是岩体动力学［1］。

边坡的地震反应分析不仅与边坡岩土体的动力特性有关，且与输入地震动力的特性密切相联［2］，远比边坡的静力分析复杂。在动力荷载作用下，边坡是否失稳的关键是岩土体对加载速率的响应：在地震中，地震波沿着坡体传输，坡体则遭受不同加载速率或应变速率的动力荷载，导致坡体内岩土体强度的明显变化［3］。

目前，研究边坡动力问题的主要方法有：拟静力法、Newmark滑块分析法、Makdisi Seed法、流动破坏分析法和动力有限元［4］。其中动力有限元是对边坡的地震反应分析行之有效的方法之一，尽管动力有限元方法计算量大，结果处理繁杂，但它可以直接求得坡体在地震荷载作用下的反应加速度、速度、位移、动剪应力和剪应变等随地震持续时间的变化过程，甚至可以求出在地震荷载作用下边坡的安全系数［5］。

2 有限元动力平衡方程

动力荷载对边坡稳定性的影响主要是：由于动荷载引起的惯性力和循环退化引起的剪应力降低，导致边坡整体下滑力增加，降低了边坡的安全系数。因此将动荷载下边坡失稳分为惯性失稳和衰减失稳［6］。

动力学问题的有限元法在考虑单元特性时，物体所受到的荷载还要考虑单元的惯性力和阻尼力等因素。其中Galerkin法和虚功原理是比较通用的方法，单元动力平衡方程式［7］如下：

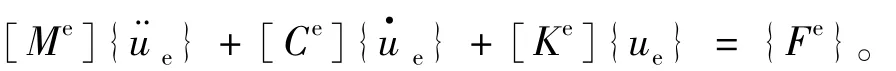
式中［Me］，［Ce］，［Ke］，［Fe］分别是单元的质量矩阵、阻尼矩阵、刚度矩阵和结点载荷向量。分别对［Me］，［Ce］，［Ke］，［Fe］进行集成形成整个系统的质量矩阵［M］、阻尼矩阵［C］、刚度矩阵［K］和结点荷载向量［F］，相应得到整个系统的动力平衡方程

3 动力有限元在工程实例中的应用

3．1 滑坡基本概况

甘肃某电站坝前约260 m左岸，发育有一方量约3 011万m3的巨型古滑坡Ⅶ＃（图1）。经“5．12”地震后该滑坡复活，滑体前缘相对滑床出现明显的剪切位移缝，缝隙延伸长度10～30 m不等，剪切位移局部可达35 cm；滑体下游区中后缘拉裂逢密集发育，滑坡后缘的陡坎高度1．5～2 m，整个滑坡目前处于蠕滑状态［8］，变形破坏迹象明显，一旦失稳将直接导致其下游的大坝失效。

图1 Ⅶ＃滑坡工程地质剖面Fig．1 Landslide engineering geological profile at Landside No．Ⅶ

3．2 动力有限元模型的建立及参数选取

由于动力有限元的计算需静力有限元作为初始条件，故仍需建立静力有限元模型。两者的区别在于参数选取和边界条件的不同，以及动力有限元需要输入地震的加速度时程曲线。静力有限元的左右边界在水平方向为固定约束，铅直方向可自由移动；动力有限元左右边界的约束条件与静力有限元相反，即铅直方向为固定约束，水平方向可自由移动（图2）；两类模型的底端均为铰支座，即水平和铅直方向均为固定约束［9］。

图2 动力有限元计算模型Fig．2 Dynam ic finite elementmodel

由于“5．12”地震的实际地震时程加速度曲线至今仍未收集到，故此处计算时采取一相近的人工合成地震加速度时程曲线（图3）作为替代，其计算结果是一致的。计算参数的选取如表1。

图3 地震加速度时程曲线Fig．3 Duration curve of earthquake acceleration

表1 动力有限元参数选取Table 1 Dynam ic finite element parameters

3．3 边坡对地震荷载的响应

计算得滑坡在地震荷载作用下的位移、加速度曲线图及最大剪应力分布分别如图4至图8。

图4 地震作用下滑坡下水平位移（单位：m）Fig．4 Horizontal displacement diagram under seism ic action（unit in m）

由图可知，滑坡体最大水平位移和最大垂直位移均出现在滑坡体的中上部，分别为0．26，0．23 m。最大水平加速度和最大垂直加速度均分布于滑坡体的中后缘坡表，值分别为3．7，2．9 m／s2。在滑面附近最大剪应力为0．002 4 MPa，受滑面形态影响，滑体中下部存在一个剪应力降低区，前缘和中上部剪应力较大。

图5 地震作用下滑坡垂直位移（单位：m）Fig．5 Vertical displacement diagram under seism ic action（unit in m）

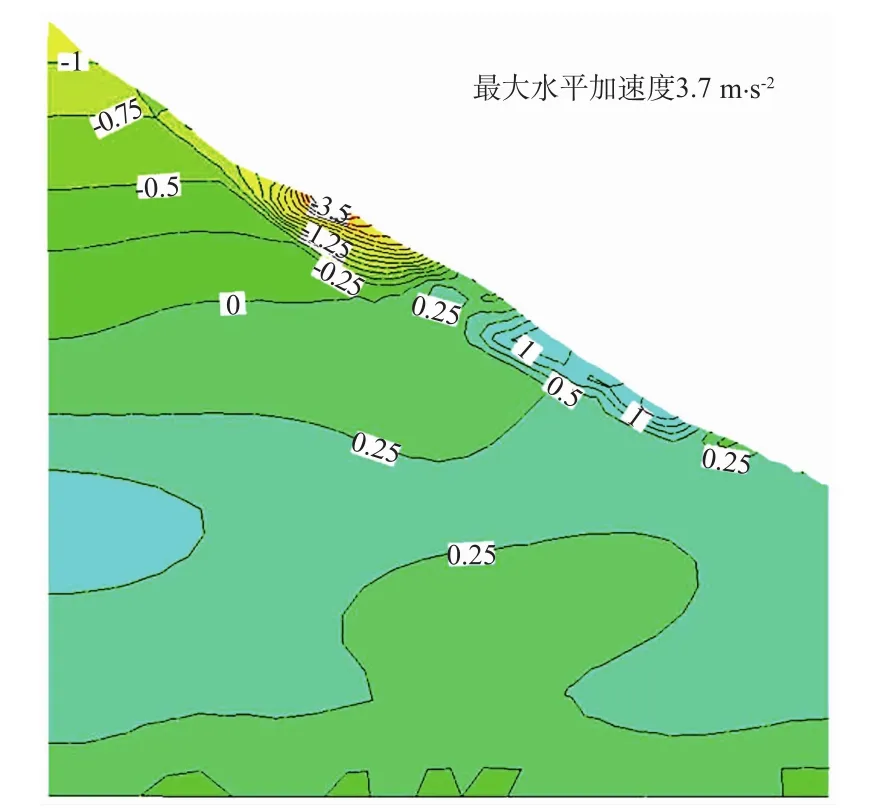
图6 地震作用下水平加速度（单位：m／s2）Fig．6 Horizontal acceleration diagram under seism ic action（unit in m／s2）

图7 地震作用下滑坡下垂直加速度（单位：m／s2）Fig．7 Vertical acceleration diagram under seism ic action（unit in m／s2）

图8 地震作用下滑面附近最大剪应力分布图（单位：MPa）Fig．8 Maximum shear stress distribution near the slip surface（unit in MPa）

以上动力有限元的计算结果表明，计算得出的Ⅶ＃滑坡在地震作用下向坡前的总体位移量约为0．32～0．37 m，与现场调查的坡体的变形破坏结果基本一致，这表明“5．12”地震是导致该滑坡复活的关键因素。

3．4 地震荷载作用下滑坡的瞬时安全性系数

应用有限元应力方法求安全系数，其安全系数（S．F．）定义为沿滑动面抗滑剪切力之和（ Sr）与沿滑动面滑动剪切力之和（ Sm）的比，即详细推导进程参见相关文献。

图9 边坡受地震作用的向坡外变形Fig．9 Deformation toward the out of landslide by the earthquake

在地震作用下，边坡受往复振荡地震波的作用，边坡会随着波的往复振荡而发生相应的瞬间变形（图9，图10）。边坡在地震荷载作用的某一瞬间，如坡体向外发生变形（图9），在滑体及滑带抗剪强度不变的情况下，边坡的稳定性在这一瞬间是降低的；反之，如坡体向坡内发生变形（图10），边坡的稳定性是增高的［10］。基于图4所示地震时程加速度曲线，计算得出该滑坡在地震荷载作用过程中的安全性系数变化时程曲线如图11，滑坡瞬时安全系数最低为0．8，最大为1．15。

图10 边坡受地震作用的向坡内变形Fig．10 Deformation toward the inside landslide by the earthquake

图11 滑坡安全系数时程变化曲线Fig．11 Factor of safety vs．time curve

4 结 语

（1）地震荷载作用下，滑体产生的位移和加速度均较滑床明显，且水平动位移及水平加速度大于垂直动位移和垂直加速度。同时，在滑体与滑床接触面附近各类等值线相对密集，这与滑体和基岩滑床的力学参数差异直接相关。

（2）地震荷载作用下引起的最大位移出现在滑体的后缘，最大水平速率出现在坡体的顶部，这两者均与物体对地震波的放大效应有关。

（3）随着坡体厚度的增加，坡体受地震作用引发的运动加速度逐渐降低。

（4）滑坡安全系数时程变化曲线的波峰、波谷位置与地震加速度时程曲线的波峰、波谷位置基本对应，这表明地震对边坡稳定性的影响是直接而明显的。同时应注意，在地震荷载作用的瞬间，边坡稳定性系数存在小于1．0的瞬间情况，但这并不意味着边坡的整体失稳。

（5）动力有限元能够准确地计算出地震对滑坡造成的位移和变形，证明了本次“5．12”地震是诱发该滑坡复活的关键因素。

［1］ 祁生文，伍法权，严福章，等．岩质边坡动力反应分析［M］．北京：科学出版社，2007．（QIWen sheng，WU Fa quan，YAN Fu zhang，et al．Rock Slope Dynamic Re sponse Analysis［M］．Beijing：Science Press，2007．（in Chinese））

［2］ 鲍叶静，高孟潭．地震诱发滑坡的概率分析［J］．岩石力学与工程学报，2005，24（1）：66－71．（BAO Ye jing，GAO Meng tan，JIANG Hui．Probabilistic analysis of earthquake induced landslides［J］．Rock Mechanics and Engineering，2005，24（1）：66－71．（in Chinese））

［3］ 万永革．地震物理过程模拟研究［D］．北京：中国地震局地质研究所，2006．（WAN Yong ge．Modeling on physical processes of earthquakes［D］．Beijing：Institute of Geology，China Earthquake Administration，2006．（in Chinese））

［4］ 徐桂弘．地震诱发滑坡的危险性分析与预测［J］．内陆地震，2008，22（2）：188－192．（XU Gui hong．Anal ysis and prediction of danger of landslide caused earth quakes［J］．Inland Earthquake，2008，22（2）：188－192．（in Chinese））

［5］ 朱大栋．复杂岩质边坡的静动力稳定性分析［D］．南京：河海大学，2007．（ZHU Da dong．Study on compli cated rock slopes of static and dynamic stability［D］．Nanjing：Hohai University，2007．（in Chinese））

［6］ 李忠生．地震作用下滑坡稳定性分析［J］．水文地质工程地质，2004，（2）：4－8．（LI Zhong sheng．Land slide stability analysis under seismic ground motion［J］．Hydrogeology and Engineering Geology，2004，（2）：4－8．（in Chinese））

［7］ 朱学贤．岩石高边坡爆破开挖安全评价［D］．武汉：长江科学院，2007．（ZHU Xue xian．Safety analysis on the dynamic stability of high rock slope induced by blasting vibration［D］．Wuhan：Yangtze River Scientific Re search Institute，2007．（in Chinese））

［8］ 张倬元，王士天，王兰生．工程地质分析原理［M］．北京：地质出版社，1994．（ZHANG Zuo Yuan，WANG Shi tian，WANG Lan sheng．Engineering Geology Theory Analyse［M］．Beijing：Geology Press，1994．（in Chi nese））

［9］ 陈昌凯．地震作用下边坡的有限元动力模拟［D］．昆明：昆明理工大学，2006．（CHEN Chan kai．Infinite element simulation on dynamic responses of slope underearthquake load［D］．Kunming：Kunming University of Science and Technology，2006．（in Chinese））

［10］刘春玲，祁生文．利用FLAC3D分析某边坡稳定性［J］．岩石力学与工程学报，2004，23（16）：2730－2733．（LIU Chun ling，QI Sheng wen．Stability analysis of slope under earthquakewith FLAC3D［J］．Chinese Journal of Rock Mechanics and Engineering，2004，23（16）：2730－2733．（in Chinese））

（编辑：赵卫兵）

Dynam ic Finite Element Analysis on Landslide Seism ic Response

LILei1，REN Guang ming1，CAOWen guang2，Zhang Ba er3
（1．Chengdu University of Technology，State Key Lab of Geological Hazard Prevention and Engineering Geological Environment Protection，Chengdu 610059，China；2．Northwest Hydro Consulting Engineers，CHECC Gansu 730050，China；3．College of Civil Engineering，Southwest Jiaotong University，Chendu 610037，China）

The seismic response of landslide is a complicated proposition，and it’s also the hot spot in recent years，especially after the“5．12”Earthquake．At present，the dynamic finite element is one of an effective way to solve the dynamic response problem of landslide．In the dynamic finite element，earthquake acceleration is themajor fac tor which reflects the seismic loading，and the impacts of the earthquake on the stress field，displacement field and velocity of the landslide．By using a giant landslide in front of some hydropower dam as an example which was in duced by the“5．12”earthquake，the seismic response analysis of the landslide has been done by a dynamic finite element software，with which the displacementacceleration and themaximum shear stress of the seismic response of the slope have been calculated．Then the status of the reciprocating vibration on the impact of the stability of land slide is illustrated．Finally，the safety factor duration curve of the landslide is got，the calculated results are con sistentwith the actual displacement of the landslide after the earthquake，it shows that the“5．12”Earthquake is the direct factor inducing the ancient landslide resurrection．

seismic load；dynamic finite element； landslide resurrection

TU457

A

1001－5485（2010）05－0053－05

2009 06 11

李 磊（1983 ），男，河南漯河人，硕士研究生，主要从事岩土体稳定性及地质灾害研究，（电话）13658019864（电子信箱）lovelil ei2008＠yahoo．com．cn。