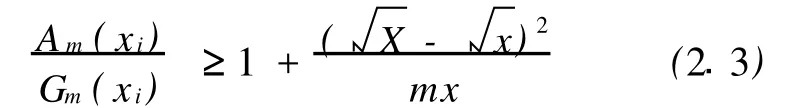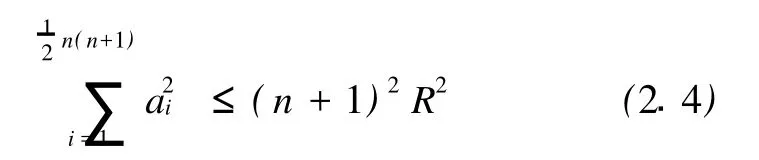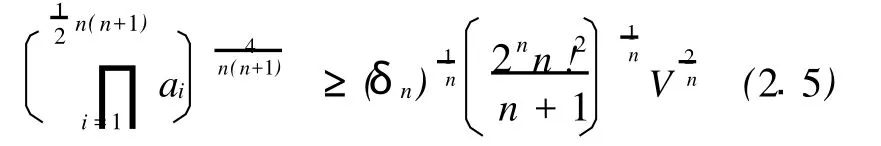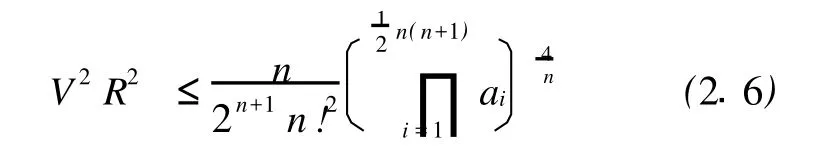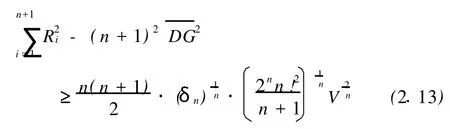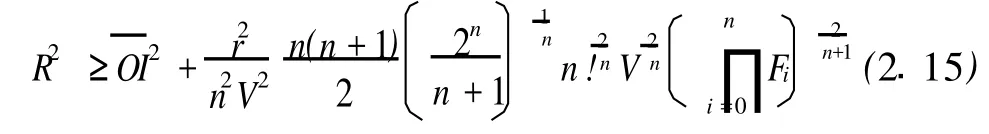关于单形的一类不等式的推广
2010-09-04杨世国
钱 娣, 杨世国
(1.安徽大学数学科学学院,安徽合肥230039;2.合肥师范学院数学系,安徽合肥230061)
关于单形的一类不等式的推广
钱 娣1, 杨世国2
(1.安徽大学数学科学学院,安徽合肥230039;2.合肥师范学院数学系,安徽合肥230061)
本文应用解析的方法得到关于单形的一类不等式的推广,并给出应用。
欧氏空间;单形;Euler不等式;体积
1 主要结果及其应用
En是 n维欧氏空间,Ωn是 En中的 n维单形。O、R分别表示单形Ωn的外心、外接球半径,I、r分别表示Ωn的内心、内切球半径,G为Ωn的重心,Ai(i=1,2,…,n+1)是Ωn的顶点,D是 En中任意一点,Ri=|DAi|(i=1,2,…,n+1)。P是Ωn内部任意一点,ri表示 P点到Ωn的第r个侧面fi的距离。单形Ωn不过同一顶点的两个棱称为一对对棱,它的各对对棱所成角的算术平均值记为θ。
1979年,Klamkin在文献[1]中得到如下的重要不等式:

其中等号当且仅当Ωn为正则单形时成立。不等式(1.1)为三角形中的 Euler不等式在 En中的推广,称为 En中的Euler不等式。
En中的 Euler不等式已引起广泛的兴趣。文献[2]中得到Euler不等式的一个加强:

当Ωn为正则单形时等号成立。
文献[3]中得到 Euler不等式的另一种加强推广:当Ωn为正则单形时等号成立。

本文得到较(1.2)、(1.3)另外一种形式的加强推广。
定理1.1 设欧氏空间 En中的n维单形Ωn的诸棱长为ai(i=1,2,…,),A=max(ai),a= min(ai),记则有

当Ωn为正则单形且 P为其内心,D为其外心时(1.4),(1.5)式中等号成立。
推论1.1 对n维单形Ωn,有

当Ωn皆为正则单形且 P为其内心,D为其外心时等号成立。
在推论1.1中,若点D、P分别是单形Ωn中的外心O和内心 I,则有 Ri=R,ri=r(i=1,2,…, n)。因此(1.6),(1.7)也是 Euler公式的两种推广形式。
推论1.2 对n维单形Ωn,有

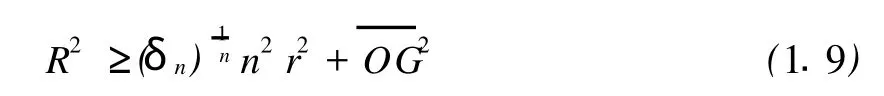
当Ωn为正则单形时等号成立。
定理1.2 对n维单形Ωn,有

当Ωn为正则单形时(1.10),(1.11)式中等号成立。
2 引理与定理的证明
为了证明上面两个定理,我们需要下面几个引理。
引理2.1[3]设 aij(1≤i 引理2.2[2]对n维单形Ωn,有 当Ωn为正则单形时等号成立。 引理2.3[4]设m个正数xi(i=1,2,…,m)的算术平均与几何平均值分别为Am(xi)与Gm(xi),X =max(xi),x=min(xi),则有 当且仅当 x1=x2=…=xn时等号成立。 引理2.4[4]设 n维单形Ωn的棱长和体积V之间有不等式 其中等号当且仅当Ωn的重心和外接球球心重合时成立。 引理2.5 对n维单形Ωn,有 当Ωn为正则单形时等号成立。 证明:应用不等式[5]: 当Ωn为正则单形时等号成立。 由(2.6)式及(2.4)式得: 即 由引理3与上式得: 由此式便得不等式(2.5)成立,易知当Ωn为正则单形时等号成立。 引理2.6[6]设 P是Ωn内部任意一点,ri表示点 P到Ωn的第i个侧面 fi的距离,V表示Ωn的体积,则有 当Ωn为正则单形时等号成立。 引理2.7[5]对n维单形Ωn,有 当Ωn为正则单形时等号成立。 引理2.8[7]对n维单形Ωn,有 当Ωn为正则单形时,式(2.9)(2.10)式中等号成立。 定理1.1的证明:由不等式(2.1)和算术-几何不等式,得: (2.11)式结合不等式(2.2),得: (2.11)式结合不等式(2.5),得: 由(2.12)式及(2.7)式便得(1.4)。 由(2.13)式及(2.7)式便得(1.5)。 定理1.2的证明:在[8]中得到不等式: 将(2.9)式结合(2.14)式得: (2.15)式结合不等式(2.9)得(1.10)。 (2.15)式结合不等式(2.10)得(1.11)。 [1] Klamkin.M.S.The circumradius-inradius inequality for a simplex,Math Magazine 52(1979),20-22. [2] 冷岗松.Euler不等式得一个加强[J].数学的实践与认识, 1995,25(2):94-96. [3] YANG Shi-guo.An Inequality for a Simplex and its Applications[J].Geometriae Dedicata,55(1995),195-198. [4] 杨世国.关于Veljan-Korchmaros不等式得改进及应用[J].纯粹数学与应用数学,2003,19(4):334-338. [5] 苏化明.关于切点单形的两个不等式[J].数学研究与评论, 1990,10(2):243-247. [6] Gerber,L..The orthocentric simplex as an extreme simplex, Pacific.J.Math,56(1975),97-111. [7] 杨世国.涉及两个n维单形的不等式[J].浙江大学学报(理学版),2006,33(3):247-249. [8] Wang Geng,Yang Shi-guo.Two Inequalities Concerning the Circumradius and Inradius of a Simplex in n-Dimensional Space [J].兰州大学学报(自然科学版),2000,36(6):18-21. Generalization of A Class of Inequalities for Simplexes QIAN Di1, YAN G Shi-Guo2 (1.School of Mathematics Sciences,A nhui University,Hef ei230039,China; 2.Department of Mathematics,Hef ei N ormal University,Hef ei230061,China) This paper discusses the improvement and application of the inequality for n-dimensional simplex in Euclidean space Enby using analytic method. Euclidean space;simplex;Euler inequality;volume O184 A 1674-2273(2010)06-0001-03 2010-03-10 安徽省高校省级重点项目(KJ2009A45) 钱 娣(1984-),女,安徽桐城人,安徽大学硕士生;杨世国(1952-),男,安徽明光人,教授,研究方向为凸几何与距离几何。