全反射平面附近的电磁真空涨落

谭美华

（湖南科技学院 电子工程系，湖南 永州 425006）

全反射平面附近的电磁真空涨落

谭美华

（湖南科技学院 电子工程系，湖南 永州 425006）

考虑了全反射平面边界附近电磁真空涨落,计算了真空涨落对带电试验粒子运动的影响,发现考虑了涨落磁场力后，试验粒子的随机运动在所有方向上都加强了，比粒子静止时更明显、更容易测量。

真空涨落；测不准关系；波包扩散；布朗运动

0 引 言

众所周知，当考虑了量子真空涨落效应时，有边界或者非平庸拓扑的平直时空与没有边界的时空（通常为闵可夫斯基时空）相比表现出不同的特征，一个著名的例子是卡西米尔 (Casimir) 效应[1]，卡西米尔效应是由于真空中两平行平面导体板改变了电磁场真空涨落引起的。真空涨落还会引起量子光锥涨落[2]。另外真空涨落还会引起真空中原子的自发辐射[3]和真空中试验粒子的布朗运动[4-6]等效应。量子涨落是任何量子场的基本特征。由于量子性质的本征属性和测不准原理，甚至在真空中量子场都存在涨落。因此我们可以期望，作为量子场涨落的结果，试验粒子将不再沿着真空中的经典轨迹运动，而是围绕平均轨迹作随机运动。类似于植物学家布朗发现的花粉颗粒在水中的无规则随机运动，所以也称荷电试验粒子的无规则随机运动为布朗运动。这种随机运动可以通过表征偏离经典平均轨迹的一些量(例如，速度和位移)的平方涨落来描述。余洪伟和Ford研究了一块全反射平面边界附近电磁真空涨落及其对荷电试验粒子运动的影响[4]和两块全反射平面导体板附近电磁真空涨落及其对荷电试验粒子运动的影响[5]，并指出了可能的实验可观测量。接着这些讨论被推广到了非平庸拓扑时空的情形，例如，空间有一维是紧致化的时空[6]。

然而，到目前为止，已有的研究都假设了试验粒子初始时是静止的。所以磁场涨落对试验粒子运动的影响被忽略了，试验粒子的位置当作了常数。如果我们去掉这些假设，并考虑到涨落磁场的贡献之后，结果将如何是非常有意思的。我们将研究在有导体平面板存在下真空量子电磁场涨落引起荷电试验粒子的布朗运动。假设试验粒子平行于平面边界以经典常速度v(例如，x方向)运动。同时考虑真空磁场涨落和电场涨落对试验粒子运动的影响。

1 全反射平面附近的电磁真空涨落

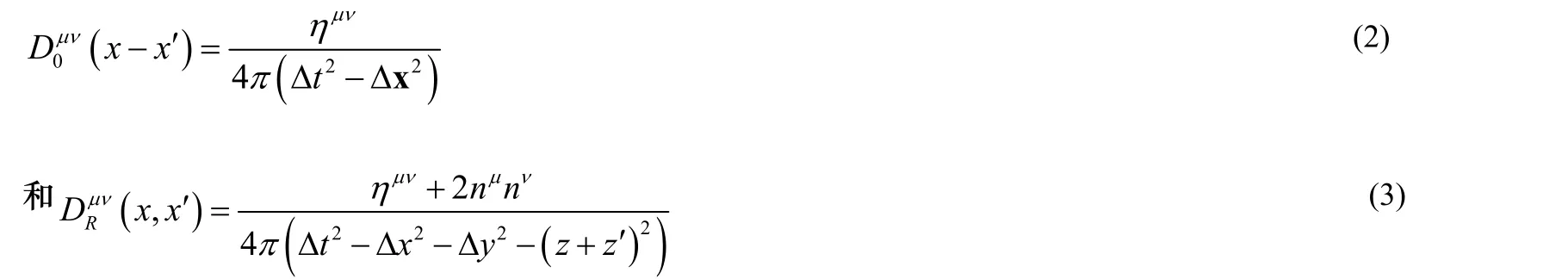
假设粒子的初始位置在(0,0,z)处，我们得到重整化之后， 电场和磁场的两点函数

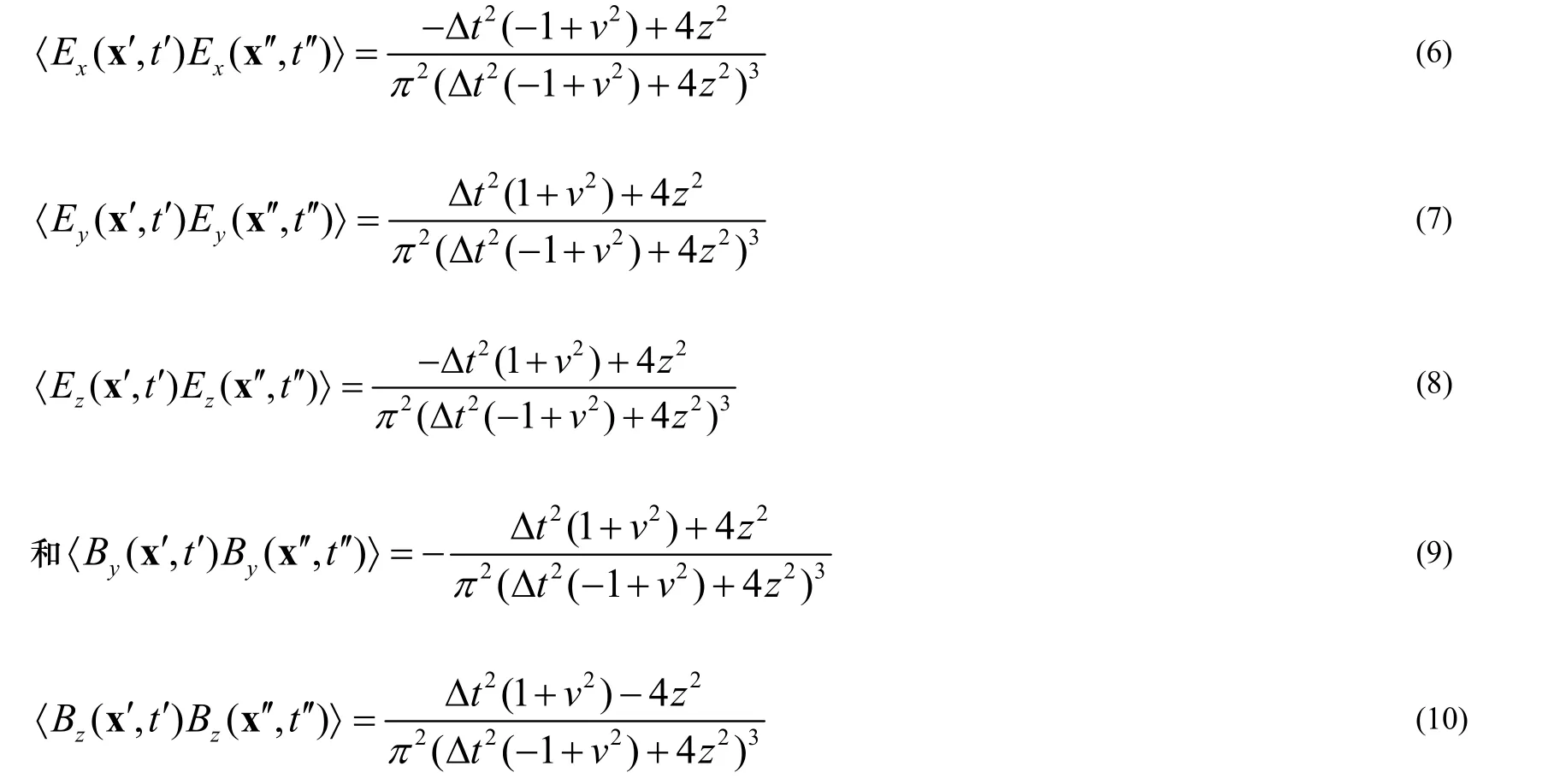
2 试验粒子的布朗运动

我们将考虑如下这种情况，即其中粒子没有明显地偏离经典轨迹，所以我们认为位置x为没有考虑量子真空涨落时的经典平均轨迹。另外，一般情况下，与相比，对磁场力的贡献可以忽略。如果粒子从开始以初速度运动，那么在t时刻速度的量子部分满足

平方速度涨落平均为

式子(13)描述粒子围绕着经典平均轨道的速度涨落。值得注意是，一般情况下，除了量子涨落场外还有可能存在经典场。把前面的两点函数(6)式～(10)式代入(13)式可得粒子围绕经典理论中平均轨道的速度涨落x方向为

相应的平均位置平方涨落x方向为

现在对上面的结果作一些解释，首先，值得注意的是，由于速度和位置涨落在纵向和横向方向都是不同的，由电磁真空涨落支配的荷电试验粒子的布朗运动是各向异性的。最明显的特征是和都是负的，这显然与直观不相符，对它的物理解释是，一个负的涨落必须表示一个不确定的减少，一种可能性是一个量子粒子的位置和速度的不确定。由于测不准原理，一个粒子的位置和速度是不能同时完全精确确定的。在量子力学中，一个有质量的粒子是用波包来描述的，它满足位置和动量的测不准原理。我们知道，随着时间的推移，波包会扩散，因此位置的不确定随着时间会增加。因此，尽管粒子原来是最小不确定波包，但是它满足测不准原理。如果我们用表示有平面边界与没有平面边界两种情况下试验粒子平方位置涨落之差，那么负的就可以理解为：波包的测不准尺度随着时间的演化比没有全反射平面的情况下的测不准尺度减小了。而在垂直于平面方向的涨落〉是正的。这说明全反射平面的存在使得在垂直于平面方向的真空涨落相对于闵氏真空中的涨落是加强的，使平行于平面方向的涨落相对于闵氏真空的涨落是减弱的。其次，与x方向和y方向的速度弥散随着时间而快速消失不同，垂直于平面边界方向的速度弥散最后趋近于非零常数。另外，与粒子静止的结果[4]相比较我们发现，含速度v的修正项与不含速度v的项有相同的符号，这表示，考虑了涨落磁场力，试验粒子的随机运动在所有方向上都加强了，这样更利于设计实验，然而，由于，与涨落电场力相比，涨落磁场力的影响一般是高阶项，因此可以忽略。最后，与经典热噪布朗运动情况不同的是，这里的平均速度平方涨落不随时间而增加，要满足能量守恒定律，因为没有使粒子获取动能的能量源。在这里不需要耗散，也不会随着时间而无限地增大，这是真空涨落量子场导致粒子的随机运动与热涨落导致的布朗运动之间明显的区别。

3 测量的可行性

值得注意是，除了涨落的量子场论力外，荷电粒子还受到一个经典点虚像电荷力的影响，虚像电荷的静电引力驱使粒子朝着全反射平面运动，并最终落向平面。为了使近似条件有意义。粒子朝着平面板的特征下落时间必须远大于z，我们可以发现条件导致，如果m表示为电子的质量，则要求，因此对于不是很轻的粒子，任何合理的实验装置都能满足条件。这里必须再次指出，我们所计算的弥散，只是描述试验粒子偏离由像电荷引起的经典轨道的位移的平均平方或速度的平均平方。

4 总 结

我们研究了一块全反射平面边界附近的真空电磁涨落及其对平行于平面以经典非零常速运动荷电试验粒子的影响，在同时考虑到涨落的电场力和磁场力时计算了带电试验粒子的位移平方的涨落和速度平方的涨落随时间变化的规律，我们的研究表明，一般的，涨落磁场对全反射平面边界附近的试验粒子速度和位置涨落的影响与涨落电场的影响相比是高阶小量，因此可以忽略。必须指出，如果速度趋近于光速时我们的结果就不再适用了，因为这时我们必须用相对论运动方程而不是非相对论运动方程了。

[1]H.B.G.Casimir. On the attraction between two perfectly conducting plates [J].Proc.Kon. Ned. Akad. Wet. B, 1948, 51(2): 793-798.

[2]Hongwei Yu, L.H.Ford.Lightcone fluctuations in flat spacetimes with nontrivial topology [J].Phys. Rev. D, 1999, 60(10): 084023.

[3]Hongwei Yu and Shi Zhuan Lu.Spontaneous excitation of an accelerated atom in a spacetime with a reflecting plane boundary[J]. Phys.Rev.D,2005,72(6):064022.

[4]Hongwei Yu and L.H.Ford.Vacuum flutuations and Brownian motion of a charged test particle near a reflecting boundary[J]. Phys. Rev.D,2004,70(9): 065009.

[5]Hongwei Yu and Jun Chen. Brownian motion of a charged test particle in vacuum between two conducting plates[J].Phys.Rev.D, 2004,70(12):125006.

[6]Chen Jun and Yu Hong-Wei.Vacuum fluctuations and motion of a charged test particle in a cylindrical spacetime[J].Chin.Phys. Lett,2004,21(12):2362-2364.

[7]Lowell S.Brown,G.Jordan Maclay.Vacuum stress between conducting plates: an image solution[J].Phys.Rev.1969,184(8): 1272-1279.

(责任编校:刘志壮)

O413.1

A

1673-2219（2010）08-0015-04

2010－5－18

湖南科技学院支持项目(08XKYTC040)。

谭美华（1980－），男，湖南郴州人，硕士，主要研究方向为天体物理。