汶川地震中高路堤的抗震响应分析

2010-09-04闵卫鲸张炳焜张建经

铁道建筑 2010年12期

闵卫鲸，张炳焜，李磊，张建经

(1.中国中铁二院工程集团有限责任公司，成都 610000;2.西南交通大学岩土工程系，成都 610031)

随着我国经济建设的飞速发展以及西部大开发战略的进一步实施，我国高等级公路建设逐渐由东部转向西部，由平原转入山区。在四川等西部山区，公路是重要的交通方式。这些地区地震频发且烈度较高，如果边坡失稳，将带来严重的后果。

目前，在工程中常利用现有规范［1-2］对高路堤边坡进行稳定性设计，大多采用拟静力法，即把地震力看作静力施加在路堤边坡上。这种方法有很大的缺陷性。由于地震荷载的随机性，以及不同的地震波有着不同的卓越周期，所以仅仅考虑峰值地面加速度 PGA(Peak ground accelearation)对结构的稳定性影响是不够的。本文利用通用大型有限元软件ABAQUS对国道213友谊隧道出口42 m高路堤边坡进行动力分析，分析比较高路堤边坡在不同地震波下的动力响应。

1 动力有限元分析理论

1.1 动力响应方程

多自由度体系在荷载下的运动方程［3］为

式中，［M］为质量矩阵;［C］为阻尼矩阵;［K］为刚度矩阵;{}为质点加速度向量;{}为质点速度向量;{u}为质点位移向量;{F(t)}是荷载随时间的函数，可以是不变量，如常荷载，也可以是可变量，如冲击荷载、谐荷载、地震荷载等。

1.2 阻尼矩阵

岩土体作为黏弹塑性体，阻尼是其重要特性。其机理十分复杂，与岩土体本身的黏性、内摩擦能量耗散等因素有关。工程实践中常用瑞利(Rayleigh)阻尼形式［8］

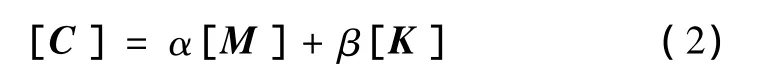
式中，α为质量阻尼系数(Alpha阻尼)，β为刚度阻尼系数(Beta阻尼)，此两系数可以通过选定岩土体的两个振型和阻尼比计算得出。联立方程为

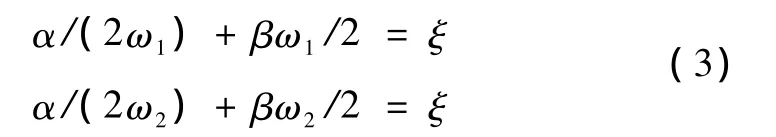
式中，ω1、ω2分别为岩土体第一、第二振型的自振频率，ξ为阻尼比。

一般情况下，可以采取简化求法，即

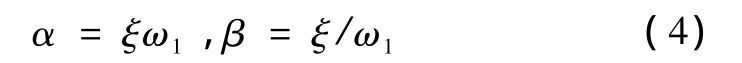
1.3 一致边界条件

边界条件在动力有限元模拟中是一个关键问题。一般认为，静力分析时选取固定边界的分析有足够的精度，但动力分析时如果边界条件仍像静力分析这样简单处理，则不能模拟出高路堤边坡的实际动力反应。地震波沿基底向上传播，到达边坡表面后产生反射，反射波向四周传播，在半无限空间中反射波可全部透射出边界，但在边界处施加位移约束后，反射波不能自由透射，再次发生反射，如此地震波在路堤体内往返反射，形成“箱效应”，导致模拟结果失真。解决“箱效应”的方法是在边界采用一致边界条件。一致边界的原理是在边界上设置弹簧—阻尼器来吸收能量和平衡位移，使其不发生再次反射。

纵波使质点沿波传播方向前后运动，剪切波使质点沿垂直波传播方向上下运动，因此，在每个边界节点处，法向切向均需设置弹簧—阻尼器［6-7］，如图1所示。

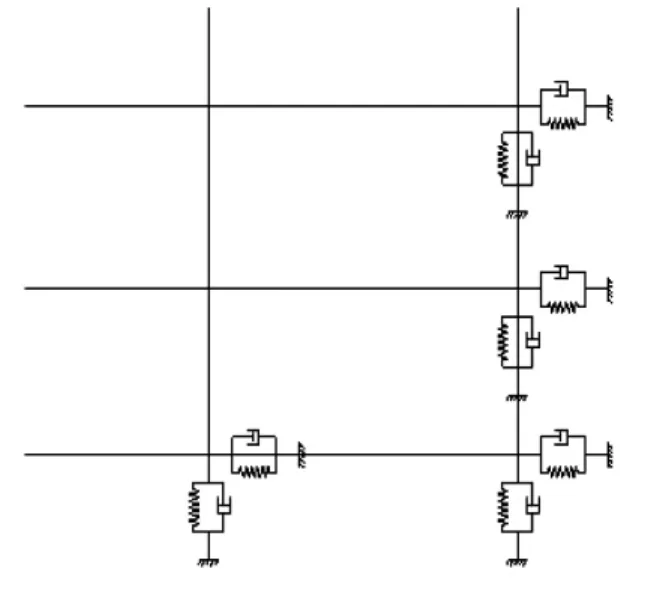
图1 黏弹性边界示意

2 高路堤边坡的材料属性

2.1 路堤填土的本构模型

Mohr-Coulomb破坏和强度准则在岩土工程和道路工程中的应用十分广泛。大量的岩土工程和道路工程设计计算都采用了Mohr-Coulomb强度准则。在本文的有限元计算中，同样采用了Mohr-Coulomb强度准则［4］。

该模型具有以下特征:①模拟材料服从经典Mohr-Coulomb屈服准则;②允许材料各向同性硬化或软化;③采用光滑的塑性流动势，该流动势在子午面上为双曲线形状，在偏应力平面上为分段椭圆形;④可与线弹性模型组合使用;⑤在岩土工程领域，可用来模拟单调荷载作用下材料的力学行为。

2.2 路堤填土的试验参数

在进行有限元分析之前，对国道213友谊隧道出口高路堤的路堤填土进行了静、动三轴试验。根据试验结果绘制动强度试验 τd/σ3c—N关系曲线，如图 2所示。

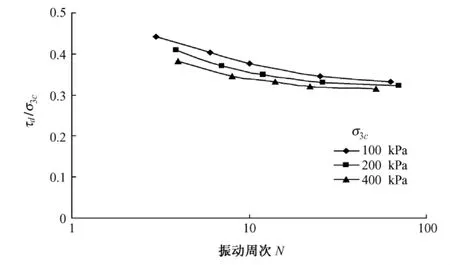
图2 动强度试验 τd/σ3c—N关系曲线

将材料对应的静三轴试验获得的抗剪强度也列于对应表1。由表1可以看出，与振动周次相对应，随地震震级增加，对应的动抗剪强度指标总体呈减小特征，且动抗剪强度指标明显低于静力抗剪强度指标。

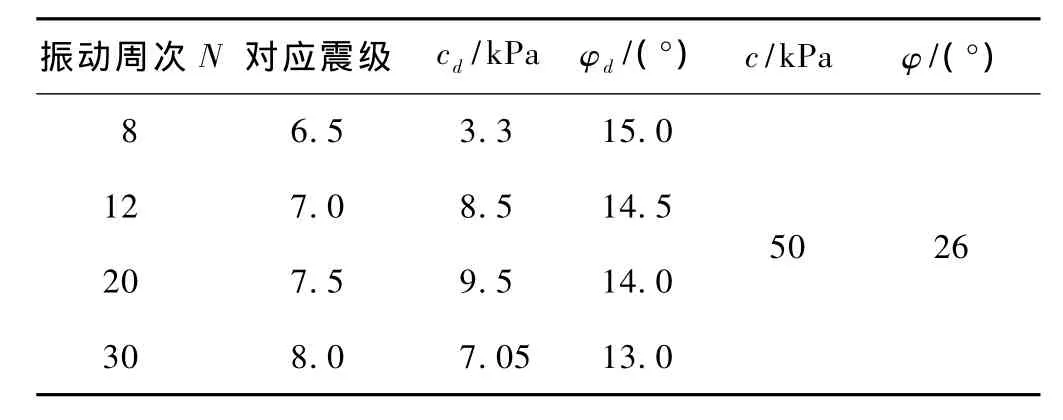
表1 材料各周次的黏聚力cd、内摩擦角φd值及静三轴黏聚力c、内摩擦角φ值

3 分析方法及模型的建立

3.1 路堤填土及下部基岩的物理力学指标

在该模型中，我们视路堤填土部分为弹塑性体，采用Mohr-Coulomb模型，将下部基岩设为线弹性体，着重考虑高路堤填土部分在强震作用下的响应问题。材料参数如表2。

表2 路堤填土及下部基岩材料参数

3.2 输入地震波的选择

本文旨在对高路堤边坡在不同特性地震波作用下的动力响应进行对比分析，故地震波的选取尤为重要。本文采用了“5.12”汶川地震中的卧龙波和1999年台湾chichi地震中的台湾波，卧龙波的 PGA=0.957 g，台湾波的 PGA约为0.4 g。为了说明高路堤在相同PGA地震波情况下的动力响应，将台湾波的加速度乘以一个系数，使其PGA=0.957 g。在此，将卧龙波和台湾波的时间分别控制在45 s和30 s，保证各自的峰值加速度在此时间段内。卧龙波和修正后的台湾波如图3。为了说明两者的不同，将两者的加速度谱绘于图4。

由图3、图4可得，卧龙波的卓越周期为0.42 s，而台湾波的卓越周期为1.14 s。由此可知，虽然两者PGA相同，但台湾波的卓越周期明显大于卧龙波。

3.3 分析模型

分析时，在ABAQUS中依照原始尺寸建立213国道友谊隧道出口处高路堤边坡模型，路堤填土高约为42 m，模型如图5。

4 分析结果及对比

4.1 高路堤边坡模态分析

图3 加速度时程曲线

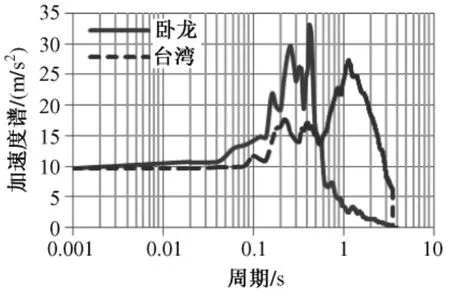
图4 卧龙波和台湾波加速度反应谱

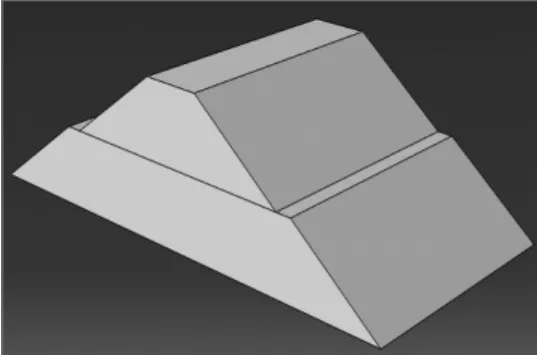
图5 高路堤动力分析的有限元模型

当材料参数和边界条件确定后，模型的特征值即确定。在对模型进行动力分析之前，先对其进行模态分析［5］，得出该路堤边坡的基频约为1 Hz，即圆频率为6.28 Hz，自振周期为1 s。可以看出，结构的自振周期与台湾波的卓越周期相近，而与卧龙波的的卓越周期相差较远。

4.2 谱加速度放大

在不同地震波下，加速度沿路堤高度的放大系数与高路堤边坡的破坏有着密切的关系。选取路堤中心线，从路堤底端中点到路面共取8个点，分别考虑每个点的谱加速度，选取 PGA、0.2 s、0.5 s、1.0 s 和 1.5 s加速度谱进行对比(以基岩上表面为基准)。结果见图6。

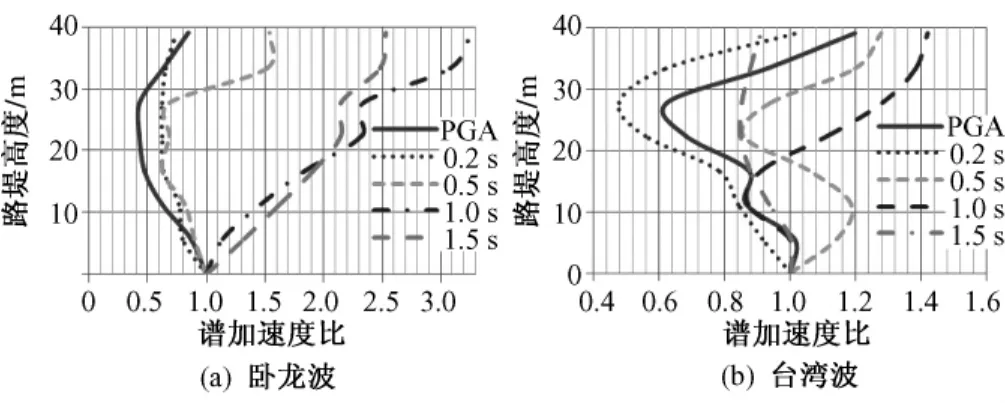
图6 至路堤中心线各点谱加速度放大比

从图6可以看出，PGA随路堤高度的变化相对于其它周期而言并不是很大，但是当周期为1 s时，加速度放大系数随路堤高度逐渐增加。而卧龙波的卓越周期为0.42 s，台湾波的卓越周期为1.14 s，其在各自加速度放大比趋势中的表现为:卧龙波，在T=0.42 s左右，其路堤面相对于基岩表面的放大比为1左右;台湾波，在T=1.14 s左右其路堤面相对于基岩表面的放大比为1.3左右。因此可以得出，在进行路堤抗震设计时，仅仅考虑PGA的作用是不够的，应当从设计谱与结构物自身特征值入手，全面权衡结构物自身特性和其所处的地域位置(是否在近缘区域和是否在地震多发带)等因素的影响。

4.3 路面竖直沉降

高速公路、铁路的沉降一直是人们关注的焦点，特别是在地震荷载作用下的不均匀沉降，将使路面结构遭到最严重的破坏。

为了对比分析结果，选取路面从左至右的若干个点，绘出路面上的竖向位移。对应于卧龙波和台湾波的路面竖向沉降见图7。

图7 卧龙波、台湾波作用下路面沉降曲线

从图7可以看出，高路堤在卧龙波下，将发生很明显的不均匀沉降，最大沉降约为22 cm，不均匀沉降量大概为15 cm。而路堤在台湾波下，不均匀沉降现象明显减弱，转而形成很明显的整体沉降，最大沉降量达到了99 cm。虽然没发生滑块的滑移破坏，但是，这也是实际工程中不允许的。

4.4 坡面水平位移

高路堤边坡坡面在地震荷载作用下所产生的水平位移也是人们很关心的问题，因为这涉及到边坡是否会发生滑坡、崩塌等灾害。该模型在卧龙波与台湾波作用下，左右坡面产生的水平位移(以基岩为基准)见图8。

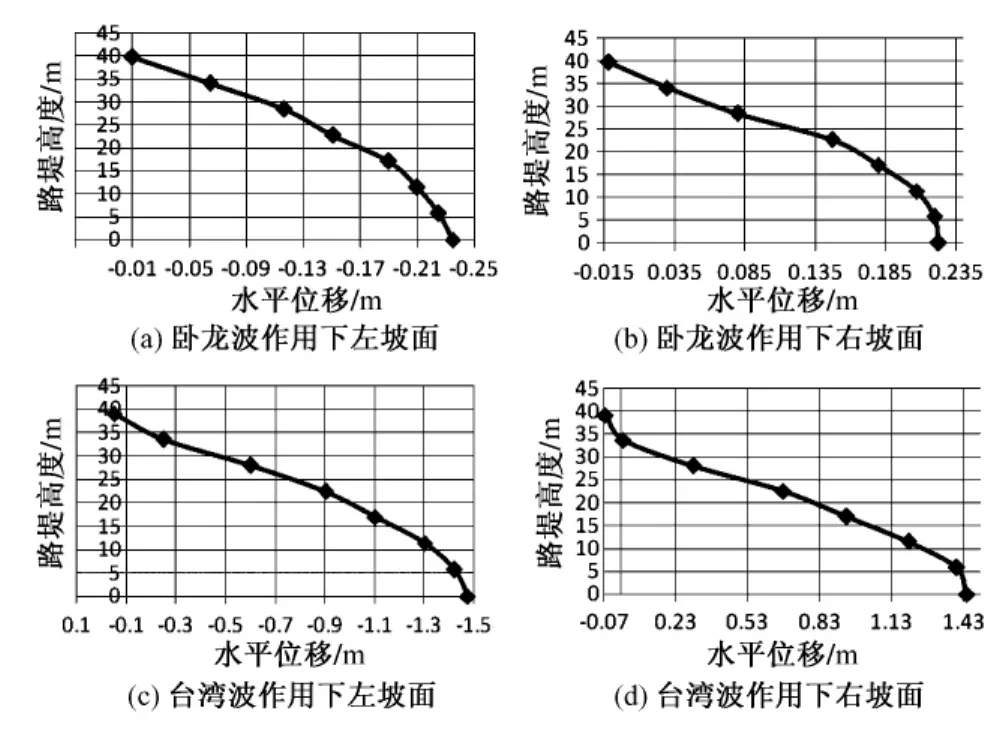
图8 卧龙波、台湾波作用下左右坡面沿高度的水平位移分布

从图8可以看出，模型左右坡面在卧龙波作用下产生水平位移较小，最大水平位移发生在坡脚处，其数值大概为23 cm;而模型在台湾波作用下，左右坡面均发生了很大数值上的水平位移，最大水平位移发生在坡脚处，数值大概为1.43 m，远远超过了工程上允许的数值范围。此时，虽然模型发生的是整体的坍塌变形，但是也视其为已经发生破坏。