基于单神经元自适应PID控制的水轮机调节系统研究

王华强, 周章海, 杨滁光

(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)

0 引 言

水轮机调节一直是水电系统中研究的重点。目前,水轮机调节系统的控制普遍采用PID控制策略。PID控制简单易行,并且能满足大多数工业过程控制的要求,但是由于水轮机的大惯性和“水锤”效应,以及各环节的非线性特性,传统的PID控制很难改善其控制品质,产生了诸如超调量大、摆动时间长、波动频繁或调节“迟钝”等现象。近几年出现了很多改进的PID控制算法,模糊控制、神经网络等智能控制技术也被应用到水轮机调节系统中,但模糊控制大多控制精度较低,多层神经网络控制理论复杂,有时难以实现。为此,本文提出了一种单神经元自适应控制方案,即在控制单元中,采用由具有自学习和自适应能力的单神经元构成PID控制器,不但结构简单,而且很好地改善了系统性能。

1 调节系统组成和基本功能

水轮机调节即随电力系统负荷变化,水轮机相应地改变导叶开度(或针阀行程),使机组转速恢复并保持为额定转速。调节的实质就是调节转速[1]。水轮机调节主要完成以下功能：

(1)随着外界负荷的变化,迅速改变机组的出力。

(2)保持机组转速和频率在规定的范围内变化。

(3)启动、停机、增减负荷,对并入电网的机组进行成组调节(负荷分配)。

水轮机调节系统主要由调节器、主接力器、引水系统及水轮发电机组等环节构成。其中,主接力器是系统的执行机构,水轮发电机组及其相关机构构成被控对象。系统结构如图1所示。

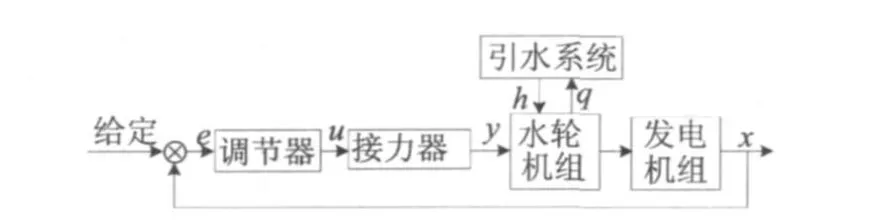
图1 水轮机调节系统结构

2 单神经元自适应PID控制策略

单神经元自适应PID控制是在常规PID控制算法的基础上,由具有自学习和自适应能力的单神经元构成自适应智能控制器[2]。单神经元PID结构简单,计算量和常规PID基本相当,实质上是一变系数的比例积分微分复合控制器。

基于单神经元自适应PID控制器的水轮机调节系统如图2所示。

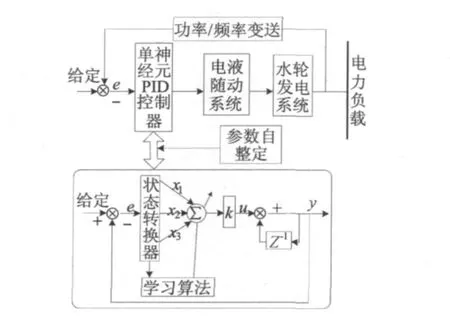
图2 水轮机的单神经元自适应PID调节原理

水轮机调节系统的主要调节量有频率和有功功率(无功功率调节由励磁系统完成)等。频率有着固定的给定值(50 Hz),而有功功率并没有固定的给定值,给定由负荷决定,当外界负荷改变时,监控工作站将根据调度需要确定当前功率调节值,然后通过网络通讯向LCU(现地控制单元)发出功率调节指令[3]。

频率调节和有功功率的调节原理基本一致,都是通过调节导叶开度调速来实现。以频率调节为例,来分析基于单神经元自适应PID控制器的水轮机调节系统的基本实现流程。

(1)当频率出现波动时,系统将进行给定频率和测量频率的比较,若两者的频率差值在一定误差范围内,则不进行频率调节控制;若两者的频率差值超过误差范围,则启动相应的频率调节控制流程。

(2)频率调节控制流程启动后,首先由单神经元自适应PID控制器实现自整定,校正控制动作,寻出最优或次优系统参数。频率误差e(k)作状态转换器的输入,状态转换器的输出即为神经元学习控制所需要的状态量：

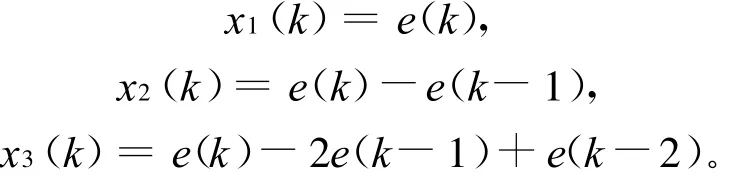
单神经元自适应控制器是通过对加权系数w(k)的调整来实现自整定,权系数的调整按有监督的Hebb学习规则实现[4,5]。有监督的Hebb学习规则是无监督的Hebb学习规则和有监督的Delta学习规则的结合。其一般性规则可描述为：

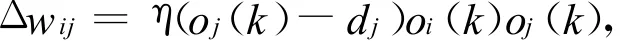
其中,wij表示神经元i和神经元j间的连接权值;oi、oj分别表示神经元i、j的激活值;dj为期望输出值。

单神经元自适应PID控制器权系数的调整是基于有监督的Hebb学习规则实现的,其控制算法及学习算法为：

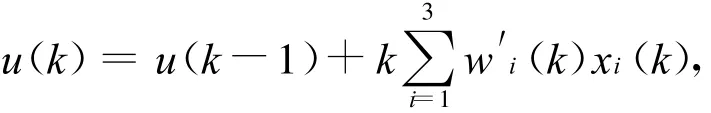
其中,

则可得：

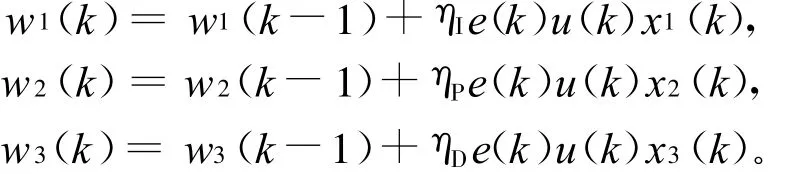
其中 ,ηI、ηP、ηD分别为积分 、比 例、微分的学习速率。

对于比例、微分、积分分别采用不同的学习速率ηI、ηP、ηD,以便对不同的权系数分别进行调整。

(3)单神经元自适应PID控制器寻出最优或次优参数后,经过运算,输出相关信号控制电液随动系统(接力器)调节导叶开度,改变机组出力恢复转速,进而保持频率的稳定。由图2及上述学习算法可知控制器的输出为：

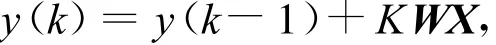
其中,K为神经元比例系数;W=[w1,w2,w3],为寻优后的权系数值;X=[x1,x2,x3],为状态向量。

综上所述,频率调节流程如图3所示。有功功率的调节过程与频率调节基本相同。

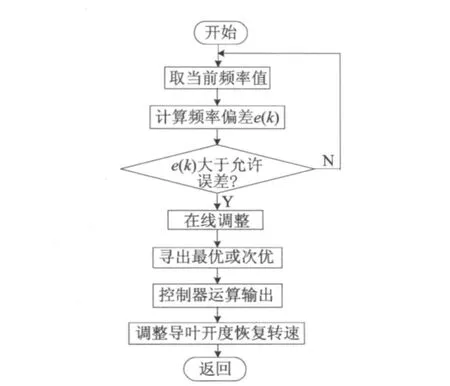
图3 水轮机的单神经元自适应PID调节流程

3 仿真分析

3.1 系统建模

一般来说,对控制系统进行计算机仿真,首先应建立系统模型,然后依据模型编制仿真程序,再对其进行动态模拟并显示结果。水轮发电机组是一个具有非线性和复杂动态性的受控对象,建立精确数学模型几乎是不可能的,但借助神经网络的建模方法和对水轮机组的简化分析,在小波动工况下,可建立系统的线性化模型[6,7]。其中转速对导叶开度的传递函数可表示为：

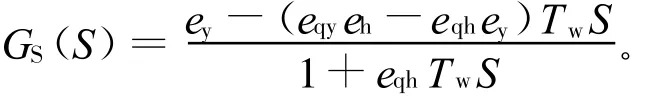
电液随动系统和发电机组可简化为一阶惯性环节,分别表示为 1/(TyS+1)和1/(TaS+en),则水轮机调节系统被控对象模型的传递函数为：

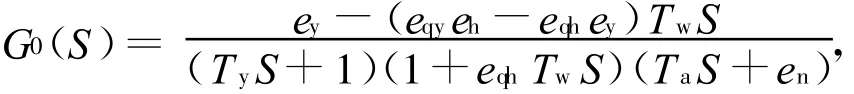
其中,Ta为机组惯性时间常数;Tw为水流惯性时间常数;Ty为主接力器时间常数;eh为水轮机力对水头的传递系数;ey为水轮机力矩对导叶开度的传递系数;en为水轮机自调整系数;eqy为水轮机流量对导叶开度的传递系数;eqh为水轮机流量对水头的传递系数。

各参数随工况的不同而发生变化,常见工况下各参数值见表1所列[8](α为导叶开度)。

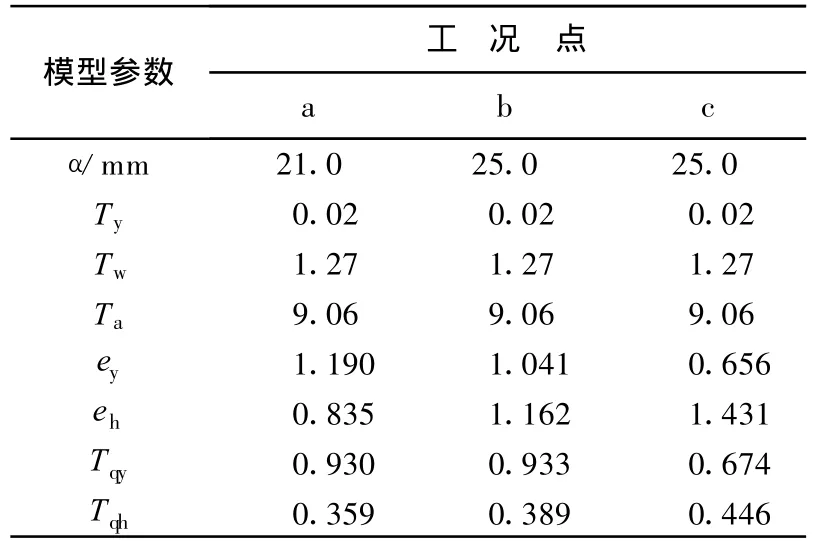
表1 某水电站工况参数表

3.2 单神经元PID和常规PID仿真分析

取导叶开度为21.0 mm(工况a)下的各参数值代入G0(S),en=0.5,传统PID控制器整定参数为KP=0.5,KI=0.2,KD=0.03;单神经元PID控制算法中的初始权值均选为0.2,比例系数K=100,学习速率 ηP=220,ηI=100,ηD=50。仿真结果如图4所示。

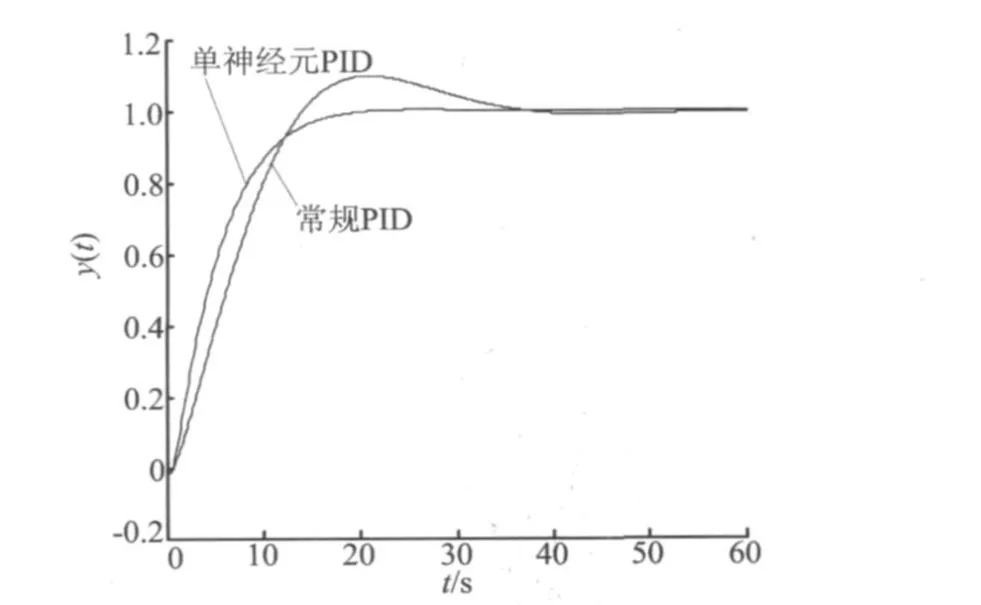
图4 单神经元PID和常规PID的仿真曲线

由图4可以看出,常规PID控制有约18%的超调量,单神经元PID控制几乎没有超调量;两者响应时间基本相同,但单神经元PID调节时间比常规PID大幅缩短。可见,相比常规PID控制,单神经元自适应PID控制系统具有更好的响应速度和动态特性。

3.3 单神经元PID和BP神经网络PID仿真

单神经元PID控制器本质上是一变系数的比例、积分、微分复合控制器,并不具备任意函数的逼近能力。多层神经网络对于复杂的非线性系统和不确定性系统,是一种解决问题的有效途径。它具有逼近任意连续有界非线性函数的能力,且具有较好的泛化功能,只要有足够多的隐层和隐节点,就可实现任意复杂的映射关系。但多层神经网络PID控制同时也存在着收敛速度慢、局部极值、隐层和隐节点难以确定等主要缺点。以典型的BP神经网络为例进行仿真说明,在水轮机调节系统中(工况a下)单神经元PID和BP神经网络PID的仿真结果如图5所示。其中BP神经网络采用3层结构,学习速率为0.26,惯性系数为0.05,加权系数初始值取区间[-0.5,0.5]上的随机数。

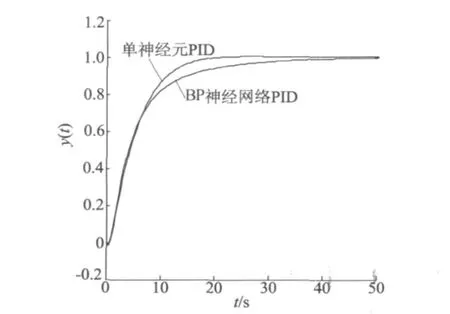
图5 单神经元PID和BP神经网络PID的仿真曲线

由图5可以看出,单神经元自适应PID和神经网络PID都取得了较好的控制效果,但神经网络PID控制的收敛速度略慢。对于复杂的非线性系统和不确定性系统,虽然神经网络PID可以逼近任意的非线性函数,但收敛速度慢的缺点将使它难以满足具有适应功能的实时控制的要求。

针对本文所讨论的水轮机调节系统,相比于较为复杂的神经网络PID控制,单神经元PID就可以很好地实现对系统的自适应控制,且算法简单明确,易于实现,收敛速度优于神经网络PID。所以对本系统而言,单神经元 PID控制更为合适。

4 结束语

由于水轮机的时变不确定性等特征,常规PID控制难以改善其控制品质,而基于单神经元自适应PID控制器的水轮机调节系统,通过在线寻优实现自适应自整定,很好地改善了系统性能,动态特性好,且相比于BP神经网络PID控制,结构简单,易于实现,是一种可行的控制策略,具有一定的工程价值。

[1]沈祖诒.水轮机调节[M].北京：中国水利水电出版社,1998：1-7.

[2]赵国山,仇性启.自适应PID的发展概况[J].化工自动化及仪表,2006,33(5)：1-3.

[3]伍 奎,李润方,蒋 卫.水电站计算机监控系统的模糊PID功率调节 [J].重庆大学学报：自然科学版,2004,27(5)：17-20.

[4]张 静.M ATLAB在控制系统中的应用[M].北京：电子工业出版社,2007：317-321.

[5]Du Chunyan,Wu Aiguo,Zheng Aihong.The application of single neuron adaptive PID method to the speed control of isothermal forging processes[C]//Proceeding s of the 6th Wo rld Cong ress on Intelligent Controland Automation,2006：21-23.

[6]王正林,王胜开,陈国顺.M ATLAB/Simulink与控制系统仿真[M].北京：电子工业出版社,2005：6-10.

[7]郭 君,董朝霞.基于神经网络的水轮发电机组的建模分析[J].电力系统及其自动化学报,2003,15(6)：37-39.

[8]张志学,李峥嵘,李朝晖.水轮机调速系统的 PID参数模糊整定[J].水电自动化与大坝监测,2002,26(1)：34-36.