反舰导弹飞行仿真方法
2010-09-02付新胜
符 燕,付新胜
(1.92941部队装备部,辽宁 葫芦岛 125001;2.92493部队 辽宁 葫芦岛 125001)
飞行仿真不仅可以精确地预测反舰导弹飞行性能,还可以在极端的战术条件下,以高置信度详尽地研究导弹性能。使用仿真方法可以减少飞行试验次数和导弹研制时间、费用,暴露系统缺陷,增大飞行试验的成功率,同时还可以获得飞行试验无法获得的飞行数据。因此,导弹研制是否从一个阶段转入下一个阶段的决策,在很大程度上是基于仿真试验的结果。与飞行试验相比,它更详细和成熟,弥补了飞行试验的不足。同时在改进导弹技术、消除错误、早期暴露其不足等方面也发挥着重要作用。
反舰导弹组成如图 1所示。主要由制导与控制、战斗部、发动机、弹体等部分组成;制导部分包括寻的装置和自动驾驶仪。
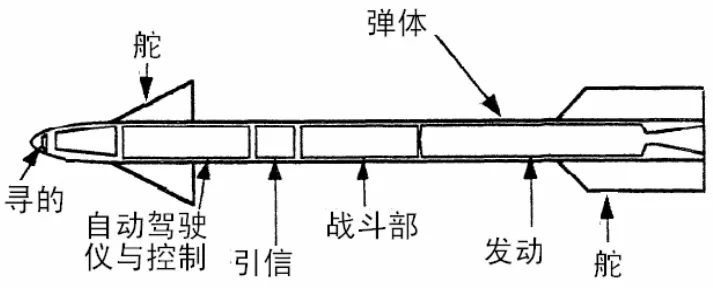
图1 反舰导弹组成框图
寻的探测目标,确定其位置,自动驾驶仪将其转换成控制指令,控制舵机偏转,使导弹向着目标方向机动。飞行仿真就是采用数学模型代替导弹的部件功能,加入环境背景、重力、空气动力学模型、目标运动模型、干扰模型,仿真导弹在作战环境中的飞行过程,检验导弹的性能。
1 仿真方法
作用在导弹上的力引起导弹产生直线加速度、转动加速度、速度和位移,这些力包括用于控制导弹飞向目标的空气动力。使用导弹运动和环境的数学模型,可以估计、预测导弹的飞行轨迹。因此需要建立制导和控制模型,作用力模型和导弹的惯性模型等,如图2所示。
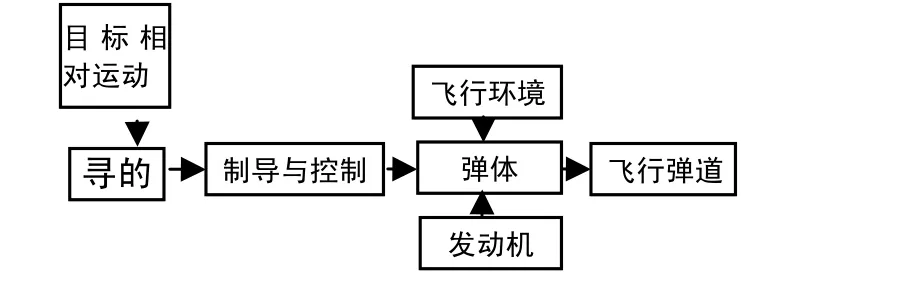
图2 导弹模型结构图
1.1 控制和制导
导弹制导程序包含寻的模型,响应由目标寻的感知的导弹与目标的相对运动产生一个导弹机动指令,送到自动驾驶程序,变换机动指令为控制指令;送到控制系统程序,计算偏转量;与空气动力学模型联合计算作用到弹体上的空气动力和力矩,进而计算导弹攻击角和空气动力升力、导弹飞行路径变化。
1)寻的
寻的模型,要求输入目标特征数据,目标场景数据,如背景、诱饵、干扰等。导弹到目标视线方向确定的目标特征数据,可以通过查表或计算得到。视线矢量、视线角,以及由寻的模型产生的目标场景特征数据,用于确定目标寻的瞬间指向。目标跟踪数据送到制导率模型中,产生制导指令。
2)自动驾驶仪与控制
自动驾驶仪和控制系统程序,通过函数变换来仿真这些分系统功能,输出为舵偏角。但在不太复杂的仿真中,不计算舵偏角,自动驾驶仪和控制系统函数模型直接转换机动指令为攻击角指令。它允许在机动指令和弹体响应之间有适当的时间延迟,以适应舵偏角、攻击角和侧向机动加速度的变化。
1.2 导弹和目标运动
导弹运动仿真的计算模型是用于计算施加在弹体上的推力、空气动力、重力和弹体运动。飞行仿真最关心的是导弹的飞行细节,而不是目标。因此目标运动往往被预先计算,它的时间序列以表格形式输入,或用非常简单的算法如直线、圆、正弦函数等表达,用于计算目标飞行轨迹。
当力加到导弹和目标的瞬间,在其质心产生一个瞬时加速度,加速度的方向与力的方向一致。如果不通过质心,将产生平移和转动。瞬时转动加速度与力的作用点到质心的力矩成比例。比例常数是转轴的力矩倒数,可以用熟悉的数学模型表示,即

式中,F为作用到导弹上的力;单位为N;m为导弹的质量,单位kg;a为平移加速度;单位 m /s2;M为作用在导弹上的力矩,单位 N.m;I为导弹的惯性力矩,单位 kg. m2;ω˙为角加速度,单位 rad /s2。
1)重力
假设坐标系固定在非转动的地球表面,x,y轴定义在地球上发射点所在平面内,假设重力矢量在运动方程中可以简化,重力矢量指向地心,幅度经过偏心修正。
2)推力
指火箭发动机作用在弹体上的力。假设推力矢量通过导弹的质心,不产生转动力矩。对于使用固态推进火箭发动机,导弹推力除时间和大气压外,所有参数的改变是独立的。推力值是在特定参考压力下时间的函数,以表格形式提供,每做一次仿真,从表中选出合适的推力值,当落在两个推力值之间时,采用插值的办法补充。当导弹高度变化时,周围大气压、导弹推力要用当前高度的大气压与参考压力进行修正,修正参数通常在参数表内,不需要计算。
对于使用其它推进方式的导弹,推力仿真更复杂,如导弹使用冲压发动机时,必须考虑速度和周围大气条件的影响。
3)空气动力
作用在导弹上的空气动力和力矩是导弹飞行速度和周围空气压力的函数。空气动力FA和力矩MA相对于这些参数的关系可以表示为:

式中,CF为空气动力系数,无量纲;CM为空气动力矩系数,无量纲;d为弹体空气动力参考长度,单位m;FA为空气动力,单位N;MA为空气动力矩,单位mN.;Q为动态压力参数,单位Pa;S为参考面积,单位m2。
CF,CM是马赫数MN和导弹控制面偏转角度的函数。而动态压力系数Q可以表示为:
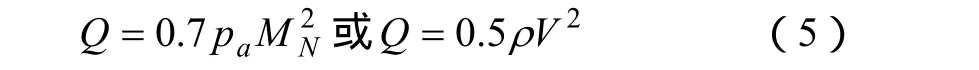
式中,pa为大气压;V为空气相对导弹弹体的速度,单位m/s;ρ为大气密度,单位kg/m2。
CFS表示每动态压力中的空气动力。参考面积S对给定的导弹,它们是常数,为导弹弹体的截面积,参考长度一般为导弹的直径。CF和CM是在亚音速条件下,相对于马赫数定义的。这些参数来源于导弹风洞试验或实际的飞行试验,是马赫数和控制面转动角度的函数。CM也取决于雷诺数,表示流体中运动惯性力与粘滞力之比,在反舰导弹仿真中,一般不予考虑。
4)弹体响应
导弹在空间里被认为是刚体,是一个有6自由度的动态系统,定义为速度的6个分量,3个为平移,3个为转动。有时根据仿真需要,忽略1个转动分量,形成5自由度模型,忽略3个转动分量形成3自由度模型。
在6自由度或5自由度仿真中,计算的每个周期内,响应自动驾驶仪指令的舵偏量都要计算。
在3自由度仿真中,不同于6自由度模型,直接假设攻击角响应寻的模型产生的侧向加速度指令。一般地,认为导弹瞬态响应特性是已知的,或可以假设,使用传递函数代替详细的空气动态响应,可以获得足够的逼真度。将攻击角指令输入到传递函数,在输出获得一个攻击角。如使用2阶系统的传递函数,允许调整指令响应时间和响应攻击角指令的攻击角值,使导弹响应特性与飞行试验数据相匹配。
1.3 仿真计算
图3为典型反舰导弹飞行仿真流程图。典型初始条件包括目标初始位置、速度矢量和导弹的位置。输入包括目标特征信号、机动参数,抗干扰参数。环境条件输入包括标准和不标准大气参数、大气变换参数。
初始化包括计算发射指向,自控飞行弹道,初始寻的指向,扫描速度,搜索角度范围。
通过查表确定大气压、空气密度和当前高度上的导弹速度。这些参数用于计算导弹的马赫数和动态压力参数。导弹发射并完成自控段飞行后,寻的开始捕获目标。导弹位置和速度矢量通常用于计算与目标速度相关的相对位置和速度,以确定导弹是否向目标接近。如果显示已经到达最近距离,停止计算,否则继续计算。要计算目标相对视线矢量的视线角,以确定跟踪误差和寻的新的指向点。把寻的输出送到制导率程序模块,产生导弹机动指令,送自动驾驶仪和控制程序模块产生舵偏角。
空气动态力矩和动力是基于当前的速度矢量、导弹高度、控制面偏差角、马赫数和动态压力参数计算的,要用周围大气压力修正当前的推力值。
导弹运动方程用于计算导弹加速度分量,将力、力矩、导弹质量、惯性力矩、角速度和重力加速度矢量等带入计算。
对导弹速度积分,计算当前时刻导弹平移、转动速度和位置。对于目标高度、速度、位置,使用相对简单的方程计算或查表。如果配置了诱饵,它们的位置、速度也要计算。在计算时间间隔内,推力分量与导弹质量减少成比例,惯性力矩和质心位置也要适当调整。当程序计算时间T超过最大飞行时间Tmax或导弹飞行高度小于地面高度时,停止程序,否则继续程序运行。

图3 反舰导弹飞行仿真流程图
2 飞行仿真中需注意的问题
在导弹研发中,研究的侧重点不同,仿真方法也不同。对目标寻的、导弹的瞬态控制、机动响应等仿真的详细程度要有所区别。如研究目标寻的跟踪方法,一般有从假设已经正确跟踪上目标,到使用实际目标寻的硬件观察在环境中辐射电磁能量的仿真目标等多种情况。研究导弹运动的方法,有简单2维模型和复杂逼真的6自由度模型等。
由仿真目的确定仿真模型,如控制面偏转,包含高频分量,需要在非常短的计算周期内进行寻的信号处理。因为处理速度慢,时间可能远大于导弹实际飞行时发生的时间,在不要求实时性的情况下是可行的。当用数学方程代替实际导弹的某些硬件时,模型在仿真计算中必须能够完成实际硬件的功能。
在导弹飞行仿真中不必要的细节可能带来大的代价,也增加了在实际中可能不出现的误差,还可能模糊一些重要仿真结果,减少程序内部相互作用的透明度,使结果分析、解释变得复杂,降低了仿真的效用,增加系统建立时间和计算运行时间。相反地,如果忽略了重要的细节,可能达不到仿真的目的,或导致对仿真结论的怀疑。这些都需要综合衡量。
3 结束语
本文给出的反舰导弹飞行仿真方法在海上靶场已经得到应用。根据不同的研究目的,建成了相应的仿真系统,成为反舰导弹研制、试验的重要工具,获得了实际飞行试验无法获得的数据,有效地减少靶场试验次数、降低试验成本。与少量的实际飞行试验相结合,可更全面地检验导弹性能和战技指标,提高了试验鉴定质量,在靶场反舰导弹试验中发挥着越来越重要的作用。
[1][俄]A.A.德米特里耶夫斯基,Л.Н.雷申科,С.С.波哥吉斯托夫. 外弹道学[M].北京:国防工业出版社,2000.
[2]赵善友,尚秉民. 防空导弹武器寻的的制导控制系统[M].北京:国防工业出版社, 1991.
[3]R. Brochu,R. Lestage. Three-Degree- of -Freedom(DOF) Missile Trajectory Simulation Model and Comparative Study with a High Fidelity 6DOF Model[J]. Defence R&D Canada - Valcartier,Technical Memorandum DRDC Valcartier TM 2003-056, December 2003.
[4]Bradford S. Canova, Peter H. Christensen, Michael D.Lee. Simulation to Support Operational Testing a Practical Application[C]. Proceedings of the 1999 Winter Simulation Conference,1071-1078, Phoenix AZ,USA, 1999.
