改进的天然气储产量生命旋回预测模型

何琰陆家亮唐红君段永刚彭炎

1.西南石油大学 2.中国石油勘探开发研究院廊坊分院

改进的天然气储产量生命旋回预测模型

何琰1陆家亮2唐红君2段永刚1彭炎1

1.西南石油大学 2.中国石油勘探开发研究院廊坊分院

何琰等.改进的天然气储产量生命旋回预测模型.天然气工业,2010,30(4):54-57.

生命旋回预测方法是目前运用最为广泛、技术成熟的油气田储产量趋势预测方法。但目前所使用的生命旋回模型在预测中难以考虑多个与储产量增长息息相关因素的影响,使得预测效果不好、精度不高。针对目前的生命旋回模型预测中存在的不足,通过储产量数据序列优化技术降低了异常数据带来的预测风险,并提出了在传统生命旋回预测模型中引入储产量增长影响因素的新方法。采用上述新方法对某气区天然气储量进行了预测,结果表明:改进的生命旋回模型对天然气的储量增长趋势预测有着很好的效果,预测结果与实际情况吻合度更高。

天然气 储量 产量 预测 生命旋回法 静态 数据 优化

1 传统生命旋回模型的弊端

传统的生命旋回模型[1-7](翁氏模型、龚帕兹模型、哈伯特模型等)预测储产量的方法,能有效控制有效资源的生命发展规律,对于中长期预测具有较好的指导作用,但存在以下不足:①均以历史数据拟合为基础,天然气储产量增长影响因素考虑有限,这种仅仅依赖历史数据序列进行单纯的数学模型拟合难免脱离生产实际;②天然气储产量增长是一个复杂的综合工程,地质条件等客观因素及认识程度、工作量等人为因素对其影响很大,如果没有把这些与储量增长息息相关的动、静态因素考虑进去,则预测效果不好,预测精度不高。

2 历史数据优化处理

由于油气田勘探开发是一项很复杂的工程,与很多不确定因素有关,因而天然气新增储产量的跃动很大,部分时间段的数据根本不能有效反映全局趋势,对预测模型构成扰动,因而本研究采用选段拟合预测的方式。在此基础上,对储产量原始历史数据进行优选及平滑预处理,达到对储产量数据整体趋势的有效把握,进而得到可靠预测结果。

2.1 分段优选

根据专家意见,选取储产量原始历史数据中对未来发展趋势有代表性的时间段,利用选取的数据段进行预测及相关分析计算。在该过程中主要注意两个方面:①数据选取段应根据当地实际生产的历史规律,将异常点尽量排除;②由于资源量的有限性,在选段计算的过程中,应当考虑排除选取段之前的探明资源量或者累计产量。

2.2 均值平滑

传统生命旋回模型是依靠研究对象的数据序列历史拟合而建立的,对历史数据序列是否平滑依赖度很高。但天然气的勘探、开发及销售等环节受到多种影响因素制约,天然气储产量时间数据序列规律性明显不强,仅仅依靠储产量历史数据拟合很难得到可靠的发展趋势。为了能更符合实际生产的发展规律,在运用传统生命模型对天然气储产量趋势预测之前,有必要对实际时间数据序列进行初步平滑优化。

以翁氏模型预测天然气储产量为例,假设天然气储产量原始历史数据序列为 Q={q1,q2,…,qn},通过历史数据拟合建立起初始模型及初步预测结果为Qt={,,…,,…}。

计算初步预测结果与原始历史数据的误差均值为:

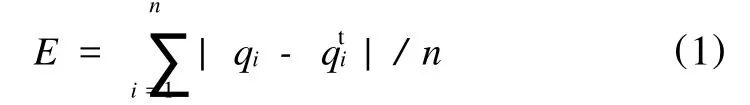
逐一考察原始历史数据序列Q中每个数据点,进行预处理:如果|qi-|>E,那么 di=;如果|qi-|≤E,那么 di=qi,其中i=1,2,…n。该点误差超出误差均值范围,则认为该点的历史数据为异常点,即不符合数据应有的整体趋势。

原始历史数据序列Q={q1,q2,…,qn}经过平滑预处理后,得到一个新的时间数据序列 D={d1,d2,…, dn},再利用生命旋回模型对新时间数据序列 D进行预测,将得到规律性更强的预测结果:QT={,,…,,…}。

3 生命旋回模型改进

3.1 影响因素权重确定

对于 Hubbert模型、广义翁氏等模型而言,静态影响因素不具备时间序列属性,模型中无法直接引进影响因素的时间序列。通过采用统计分析法给出影响因素对预测变量的权重估计,结合层次分析法等专家干预手段确定最终的影响权重。这样不仅保证了预测变量历史发展的规律性,也将专家意见有效引入,确保预测的有效性和权威性。

假设:Q(i)为时间序列上某一年的年新增储产量实际值,Qa(i)为其传统预测模型预测值,如果预测精度达到100%,那么有:

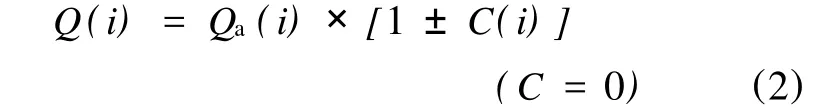
事实上,预测误差幅度C(i)≠0,而预测误差幅度C(i)是由影响因素产生的。系统通过误差幅度序列平均值作为引入影响因素,修正误差权重参考值,有效降低预测误差。如何确定系统给定的影响因素权重范围呢?

令 E∈[-e,+e],E即为影响因素权重。则年新增储产量实际时间序列值为:Q={Q(1),Q(2),…, Q(n)};年新增储产量预测时间序列值为:Qa= {Qa(1),Qa(2),…,Qa(n)}。那么,

3.2 影响因素权重分配

通过上述方法确定权重的范围后,专家可根据经验指定影响因素总体权重,但是不能超出该权重的变化范围,否则视为误操作。在此基础上,采用层次分析法对影响因素进行权重分配。

3.2.1 建立层次结构模型

所建立层次结构模型见图1。

图1 层次分析法结构示意图

3.2.2 构造成对比较矩阵

设储产量预测中共有 n个影响因素,那么 X= {x1,x2,…,xn},在实例中,x1是资源量,x2为探明程度,xn为勘探思路及勘探技术。构造判断矩阵[8]:A= (aij)n×n。比较每个因素对上一层某一准则(或目标)的影响程度,确定各因素在该层中相对于某一准则所占的比重,即aij表示第i个因素相对于第j个因素对目标层的影响重要程度,若 ai和aj同等重要为1,ai比aj稍微重要为3,ai比aj重要为5,以此类推,若处于其中,可取2、4、6、8,令

可得成对比较判断矩阵:

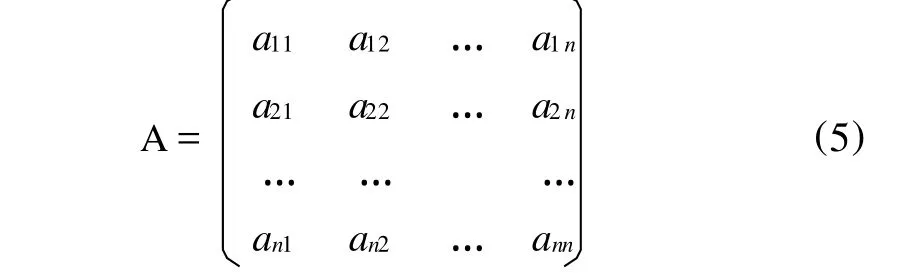
3.2.3 影响因素权重分配

用定义计算矩阵的特征值和特征向量相当困难,特别是阶数较高时;成对比较矩阵通过定性比较得到结果,对它进行精确计算没有必要。鉴于此,采用最为常用的“求和法”计算成对比较矩阵的相关值。具体办法如下[8]。

1)将矩阵列向量归一化

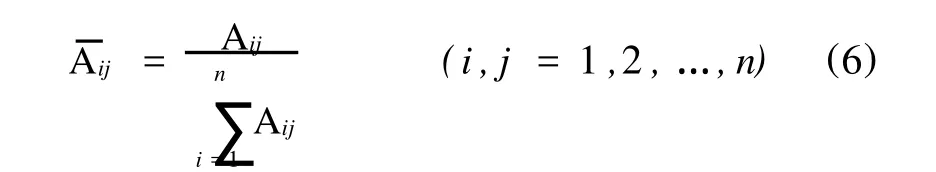
2)将归一化的判断矩阵按行相加

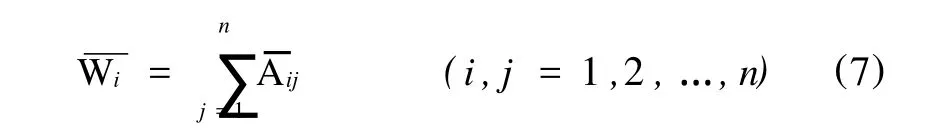
3.3 影响因素敏感性分析

基于科学假设,认为模型误差完全由全部影响因素所致,具体体现在模型的误差均值中,对于给出的影响因素在中的程度由层次分析法得到。不同的影响因素及权重系数可以得到不同的 ET,即得到更为合理的拟合数据序列。

具体分析过程如下。

第一步:对原始时间数据序列进行分段优选,得到分析时间数据序列段Q={q1,q2,…,qn}。

第二步:进行第一次校正拟合,得到初始预测序列Qt={,,…,,…}。

第三步:应用历史数据序列段优化方法,得到新的时间数据序列QT={q1T,q2T,…,qnT}。其中qiT根据 E/n得到,如果|qi-|>E,其中i=1,2,…,n,那么 qiT=,否则 qiT=qi。

第四步:根据影响因素(气藏地质条件、市场需求、政策等),运用层次分析法,得到 ET= EW=w/n,其中 ET为专家赋予权重的数据修正范围,W为权重方案。

第五步:根据因素影响程度的大小,可分为影响因素正向极大、正向较大、正向较小、负向极大、负向较大、负向较小等多种层次,运用层次分析法即可得到多个权重方案(W1,W2,Wk),根据第三、四步,可以得出对应的多种权重方案下的多个更具合理的修正序列。

气藏条件正向极大:Q1={q11T,q12T,…,q1nT}。

气藏条件正向较小:Q2={q21T,q22T,…,q2nT}。

气藏条件负向较小:Q3={q31T,q32T,…,q3nT}。

运用预测模型对上述多种影响程度下优化序列进行模拟预测,得到多种预测趋势(体现在模型参数变化中),进而得到综合分析中影响因素变化下的多种趋势预测结果。

4 改进方法预测实例

根据上述方法,在WINDOWS下基于ORACL E、ACCESS数据库,用VB.NET语言开发了一套天然气储量产量中长期变化趋势预测的软件系统。通过该软件系统,将上述方法应用到国内某气区,通过探明储量预测实例来检验改进方法的适用性。

4.1 资源量(地质因素)的影响

由图2不难看出,资源量越大,预测模型曲线的凹凸性越显著,年新增储量达到峰值的时间越靠后,峰值也越大。因此,同样的原始数据,使用同样的模型,资源量不同时预测结果是不同的。因此,在储产量预测时一定要考虑资源量(地质因素)对预测结果的影响。

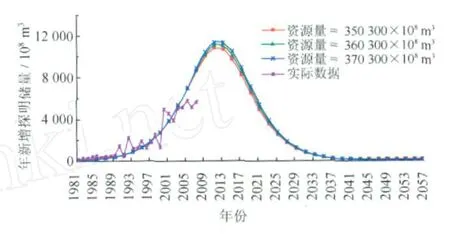
图2 同种模型中不同资源量及相同资源探明率的预测图

4.2 探明程度(地质因素)的影响

从图3不难看出,较高探明程度时,年新增探明储量的峰值更高、达到峰值的时间越长。在相同经济技术状况下,探明程度为35%的预测曲线显示,天然气年新增探明储量在2009年达到峰值6325.8×108m3;探明程度为45%的预测曲线显示,天然气年新增探明储量2010年达到峰值8123.2×108m3;探明程度为55%的预测曲线显示,天然气年新增探明储量大致将在2011年达到峰值9930.5×108m3;探明程度为65%的预测曲线显示,天然气年新增探明储量大致将在2012年达到峰值11748.0×108m3。探明程度越大,峰值越大,达到峰值的时间越长。因此,同样的原始数据,使用同样的模型,探明程度不同时预测结果是不同的。因此,在储产量预测时一定要考虑探明程度对预测结果的影响。

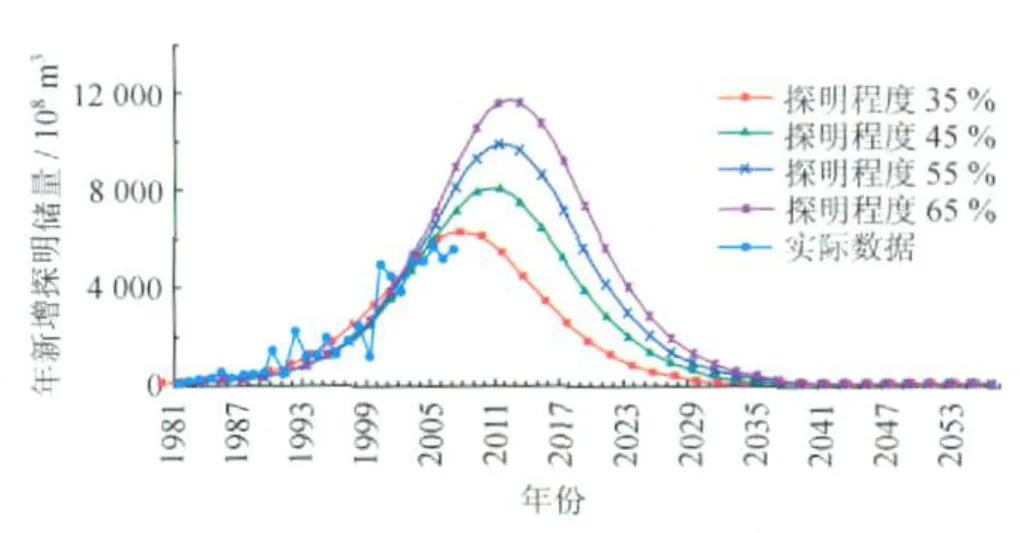
图3 不同探明程度下的预测数据结果曲线对照图

4.3 市场需求、新技术等因素的影响

每一个影响因素对储产量都会产生正向或负向的影响。利于储产量增长的因素,在一定程度上应该加快其峰值的到来时间,而弊于储产量增长的,在一定程度上则会延缓顶峰到来的时间。新技术、市场需求、工作量、国家政策等因素均具有双重性,将利于储量增长的,称为储量增长正向影响因素,反之为储量增长负向影响因素。本实例仅以“新技术”为例,结合层次分析法,将其引入传统生命旋回预测模型中,说明其对新增探明储量的影响。

从图4可以看出,在正向影响因素(新技术)增大的情况下,龚帕兹曲线更早达到峰值。也就是说,正向的影响因素(如市场需求增大等)会迫使人们采取相关措施加大勘探力度(增大工作量),使用新的勘探技术等。这些因素的必然结果就会使得天然气探明气区面积增加、探明程度提高,当然储量增长就加快,在其他条件相同的情况下,峰值到达时间就越早;反之,市场需求变小,新增探明储量的峰值时间自然会适当延后。

图4 相关影响因素(新技术)敏感度预测图示

以上分析可以看出,新技术、市场需求、工作量等因素均会影响预测结果。因此,在进行储产量中长期预测时应考虑这些因素的影响。

4.4 常规模型与改进后模型的对比

从表1可以看出,进行了数据处理以及引入影响因素的改进模型比常规的生命旋回模型的相关度好,峰值时间与实际情况也更吻合。

表1 某气区天然气新增储量传统模型与改进模型预测结果对比表

5 结论

1)资源量越大,预测模型曲线的凹凸性越显著,年新增储量达到峰值的时间越靠后,峰值也越大。

2)探明程度越高,年新增探明储量的峰值越高、达到峰值的时间越长。

3)正向的影响因素(比如市场需求增大,勘探力度加大,新技术的开发使用,勘探思路的转变等),这些因素影响的必然结果就会使得天然气探明气区面积增加、探明程度提高,当然储量增长加快;在其他条件相同的情况下,峰值到达时间就越早;反之,市场需求变小,新增探明储量的峰值时间自然会适当延后。

4)从以上分析可以看出,地质因素(资源量、探明程度)、新技术、市场需求、工作量等因素均会影响预测结果,因此,在进行储产量中长期预测时应考虑这些因素的影响。从预测结果可以看出,进行了数据处理以及引入影响因素的改进模型比常规的生命旋回模型的相关度好,峰值时间与实际情况也更吻合。

[1]翁文波.预测论基础[M].北京:石油工业出版社,1984.

[2]陈元千.广义翁氏预测模型的推导与应用[J].天然气工业,1996,16(2):22-26.

[3]张抗.油气田的生命周期和战术战略接替[M].北京:地质出版社,2000.

[4]王思聪,冯连勇,赵林.石油峰值问题及油气田生命周期理论研究——中外石油专家石油峰值理论要论评析[J].石油科技论坛,2006(2):27-32.

[5]张抗,周总瑛,周庆凡.中国石油天然气发展战略[M].北京:地质出版社,2002.

[6]董蔚凯,靳涛,王屿涛,等.准噶尔盆地油气储量、产量增长趋势预测[J].新疆石油地质,2007(5):622-624.

[7]隋风贵,罗佳强.应用翁氏旋回模型预测济阳凹陷的最终勘探储量[J].成都理工大学学报:自然科学版,2003(2):175-177.

[8]演克武,朱金福,何涛.层次分析法在多目标决策中的不足与改进[J].统计与决策,2007(9):10-11.

DOI:10.3787/j.issn.100020976.2010.04.012

He Yan,associate professor,was born in1971.He holds a Ph.D degree and working as a postdoctoral at the station,being engaged in comprehensive research in petroleum geology.

Add:No.8,Xindu Avenue,Xindu District,Chengdu,Sichuan610500,P.R.China

Tel:+86228283032276 E2mail:swpuheyan@163.com

An improved lifecycle model for predicting natural gas reserves and production

He Yan1,Lu Jialiang2,Tang Hongjun2,Duan Yonggang1,PenYan1
(1.Southwest Petroleum University,Chengdu,Sichuan610500,China;2.L angf ang B ranch,Research Insti2tute ofEx ploration and Development,PetroChina,L angf ang,Hebei065007,China)

At present,the life2cycle model is a mature technology and has been widely used for forecasting oil and gas reserves and production trend.However,the life2cycle model currently used cannot take account of many influencing factors closely interrelated to reserves and production growth,so it will result in low accuracy and bad results in prediction.Therefore,aiming at the deficiencies in the current life2cycle model,an optimization technique on reserves and production data array has been used to mitigate the forecas2ting risk brought by the abnormal data.Moreover,a new method has been proposed,which introduces the influencing factors of re2serves and production increment into the traditional life2cycle model.A case study in a gas field was performed by this improved life2cycle model with good forecasting results,which showed a good coincidence with the actual results.

natural gas,reserves,production,prediction,life2cycle model,static data,optimization

book=54,ebook=369

10.3787/j.issn.1000-0976.2010.04.012

2009-11-09 编辑 韩晓渝)

中国博士后基金项目(编号:国201,中博基字〔2006〕17号20060400307);国家重大专项基金项目(2008ZX05007)。

何琰,1971年生,副教授,博士,在站博士后;从事石油地质综合研究工作。地址:(610500)四川省成都市新都区新都大道8号。电话:(028)83032276。E-mail:swpuheyan@163.com

NATUR.GAS IND.VOLUME30,ISSUE4,pp.54257,4/25/2010.(ISSN100020976;In Chinese)