单位圆上调和拟共形映照的复特征估计

朱剑峰

（华侨大学数学科学学院，福建 泉州 362021）

单位圆上调和拟共形映照的复特征估计

朱剑峰

（华侨大学数学科学学院，福建 泉州 362021）

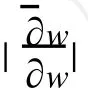
调和映照；拟共形映照；伸缩商；偏差估计

单叶调和函数与单叶函数论、调和分析、拟共形映照理论都有密切的联系.近年来，对单位圆上单叶调和函数的研究非常活跃，特别是w=P［f］（z）在何种条件下成为调和拟共形映照，有很深入的研究.文［1-3］给出了w=P［f］（z）成为调和拟共形映照的充要条件，但对其复特征模的估计没有涉及；文［4-7］研究了w为调和k-拟共形映照的的一些相关性质；文［8-9］估计了两类单叶调和映照的偏差估计.本文研究w的边界函数，给出w为拟共形映照时其偏导数及复特征模的估计.

1 基本假定

以下不另做声明，均假设f（x）=exp［iγ（x）］.定义w=u+iv为平面区域Ω上的单叶调和函数.若Ω为单连通区域，则存在h（z），g（z）为Ω上的解析函数，使得w=h+.

则由Lewy定理可知，w=P［f］（z）是单位圆D内的单叶调和函数.

令f（x）=exp［iγ（x）］，x∈R，满足f（x±2π）=exp［iγ（x±2π）］=f（x）.如果γ（x）在区间［0，2π］绝对连续，则对于几乎所有的x∈［0，2π］，有

2 主要结果及其证明

证明 设w=P［f］（z）=u+iv，则由式（1）可知，对于任意的z=rexp（iγ）∈D，有

而且有

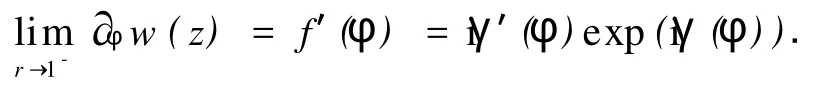
于是，有

注意到u（exp（iφ））=cosγ（φ）及v（exp（iφ））=sinγ（φ），所以有

式（4）中，K（x，φ）=γ′（φ）-γ′（φ）cos（γ（φ）-γ（x））≥0.因为有

所以，利用w（0）=0，可得到

另一方面，如果|f′（x）|≤A，则有如下引理.

证明 由式（4）可知

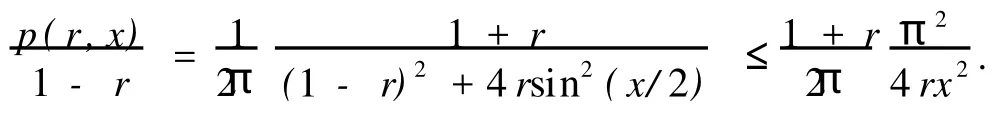
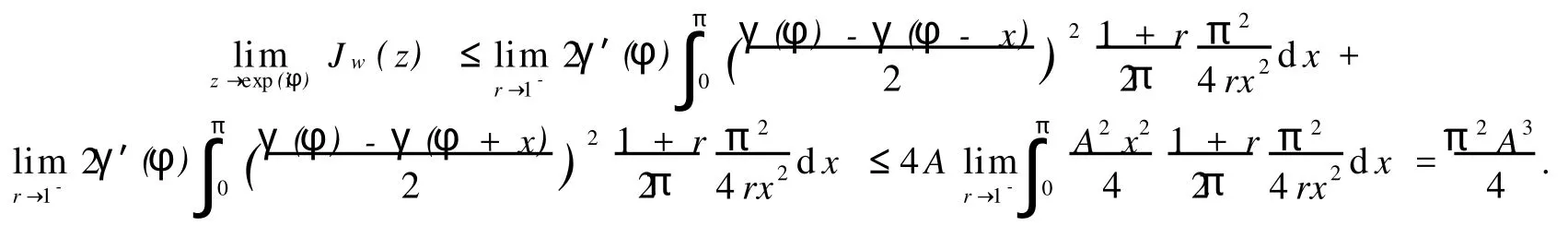
有了引理1，引理2，下面证明两个主要结果.

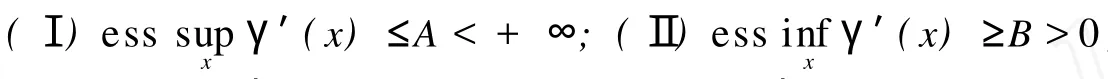
证明 由式（2），（3）可得

且

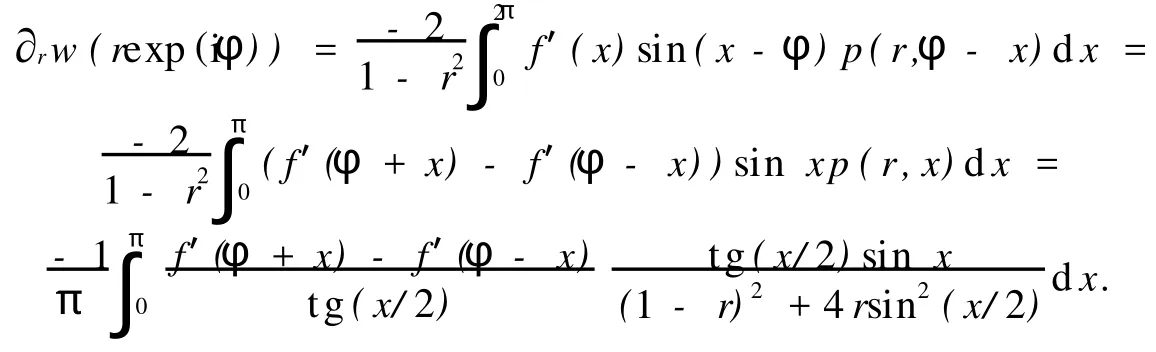
所以，有

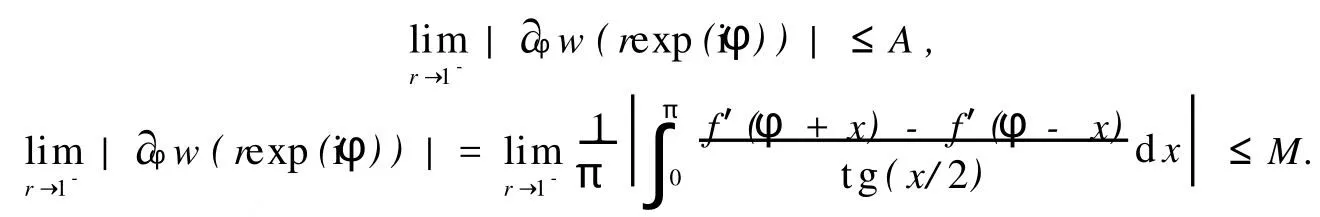
人为因素也是影响畜牧养殖业动物发病的一个重要原因，由于农户的科学养殖意识不高，对养殖设施的设置不全面以及用药和管理不当等，都是造成动物发病的重要人为因素。同时，农户在进行养殖前选址不当也是造成动物发病率较高的一个因素。在动物疾病的防控中，很多养殖人员缺乏专业的动物疾病防控知识，出现疫情乱用药等也会加重疫情的传播，导致不良后果的出现。另外，养殖中缺乏专业的消毒措施也是使目前动物疫情频发的重要人为原因。

对于定理1中的3个条件，文［1］已证明了w具有拟共形的性质，也就是说，条件（Ⅰ），（Ⅱ），（Ⅲ）是w为调和拟共形映照的充要条件.但是，文［1］中没有涉及到对|h′（z）|及一些相应量的估计.针对以上一些量的估计，进一步的研究得到如下的定理.

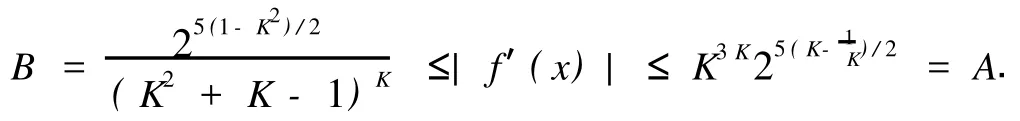
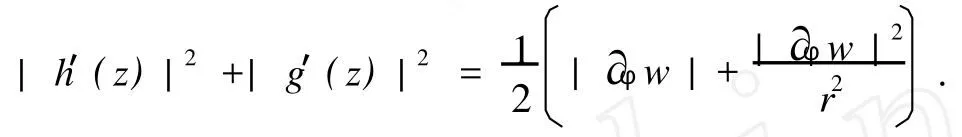
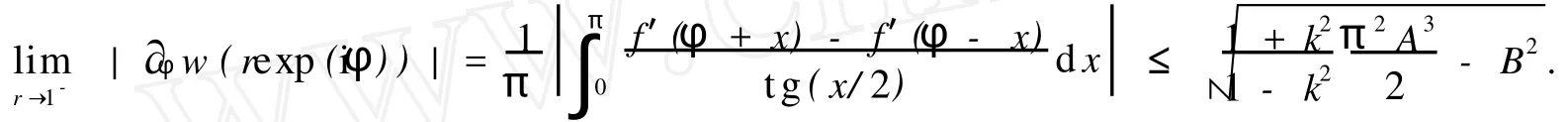
证毕.

［1］PAVLOVIC M.Boundary correspondence under harmonic quasiconformal homeomorphisma of the unit disk［J］.Ann Acad Sci Fenn（Series A1）：Math，2002，27（2）：365-372.

［2］KALAJD.Quasiconformal harmonic functions between convex domains［J］.Publications De L’Institut Mathématique，2004，76（90）：3-20.

［3］PARTYKA D，SAKAN K.On an asymptotically sharp variant of Heinz’s inequality［J］.Ann Acad Sci Fenn（Series A1）：Math，2005，30（1），167-182.

［4］PARTYKA D，SAKAN K.On bi-lipschitz type inequalitites for quasiconformal harmonic mappings［J］.Ann Acad Sci Fenn（Series A1）：Math，2007，32（2）：579-594.

［5］BEUELING A L，AHLFORS V.The boundary correspondence under quasiconformal mapping［J］.Acta Math，1956，96（1）：124-142.

［6］L ETHO O.Univalent functions and teichmuller spaces［M］.New York：Spring-Verlag，1987.

［7］CLUNIE J，SHEILl-SMALL T.Harmonic univalent functions［J］.Ann Acad Sci Fenn（Series A1）：Math，1984，9（1）：3-25.

［8］吴瑞溢，黄心中.Salagean类单叶调和函数的特征［J］.华侨大学学报：自然科学版，2008，29（2）：308-311.

［9］韩雪，黄心中.两类单叶调和函数的偏差估计［J］.华侨大学学报：自然科学版，2008，29（4）：618-621.

Estimate for the Dilatation of Harmonic Quasiconformal Mappings in the Unit Disk

ZHU Jian-feng
（School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China）

Letf（x）=exp（iγ（x））be a sense-preserving homeomorphism of the unit disk，w=P［f］（z）be a harmonic mapping of the unit disk onto itself with boundary valuesf（x）.In this article，by studying the boundory functionf（x），we obtain a good estimate forJw.Ifwis a harmonic quasiconformal mapping，the complex dilatation ofw.

harmonic mapping；quasiconformal mapping；dilatation；distortion estimate

O 174.55

A

1000-5013（2010）04-0476-04

（责任编辑：陈志贤 英文审校：张金顺，黄心中）

2008-09-14

朱剑峰（1980-），男，讲师，主要从事函数论的研究.E-mail：flandy@hqu.edu.cn.

华侨大学科研基金资助项目（08HZR19）