采用积累弦长法拟合3次NURBS曲线
2010-08-30叶丽谢明红
叶丽,谢明红
(华侨大学机电及自动化学院,福建 泉州 362021)
采用积累弦长法拟合3次NURBS曲线
叶丽,谢明红
(华侨大学机电及自动化学院,福建 泉州 362021)
根据已知的3次非均匀有理B样条(NURBS)曲线型值点,采用效果较好的积累弦长参数化方法构造节点矢量,从而得到B样条基;利用带权控制顶点的矩阵计算出全部控制顶点,最后拟合出所要求的曲线.拟合结果表明,该方法可以反映数据点按弦长的分布情况,适用于构造任意次非均匀有理B样条曲线节点矢量参数的计算,较好地适合于工程实践的应用.
非均匀有理B样条;积累弦长;参数化;型值点;控制顶点;曲线拟合
CAD系统在设计自由曲面零件时,由于缺乏传统方法的触觉和视觉优势,因此常采用粘土等材料进行传统的手工设计,然后利用曲线曲面反求技术将其转化为计算机可用的CAD模型.反求技术可以极大地缩短产品周期,更重要的是可以快速赶上或超过世界先进生产技术水平.STEP(Standard Exchange of Product Data Model)国际标准中关于工业产品几何定义的统一数学方法——非均匀有理B样条(NURBS)方法为标准解析形式的初等曲线曲面、自由型曲线曲面的精确表示和设计提供了一个公共的数学表示.NURBS曲线曲面在实际应用中可以分为两种形式[1]:一种是已知控制点求解曲线曲面上的点,称为正算问题;另一种情况是已知曲线曲面上的型值点求解曲线曲面的控制点,称为反算问题.本文只讨论3次NURBS曲线问题.
1 3次NURBS曲线
由n+1个多边形控制顶点定义的1条k次NURBS曲线[2],可以表示为1条分段有理多项式矢函数,即
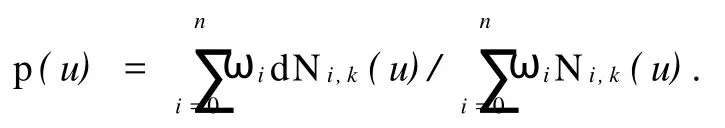
式中:ωi(i=0,1,…,n)为权或者权因子,分别与控制顶点d(i=0,1,…,n)相联系;首、末权因子ω0,ωn>0,其他ωi≥0,顺序k个权因子不同时为零,以防止分母为零,保留凸包性质,曲线不致因权因子而退化为一点.Ni,k(u)是由节点矢量U=[u0,ui,…,un+k+1],按德布尔-考克斯递推公式决定的k次规范B样条基函数.其递推公式为
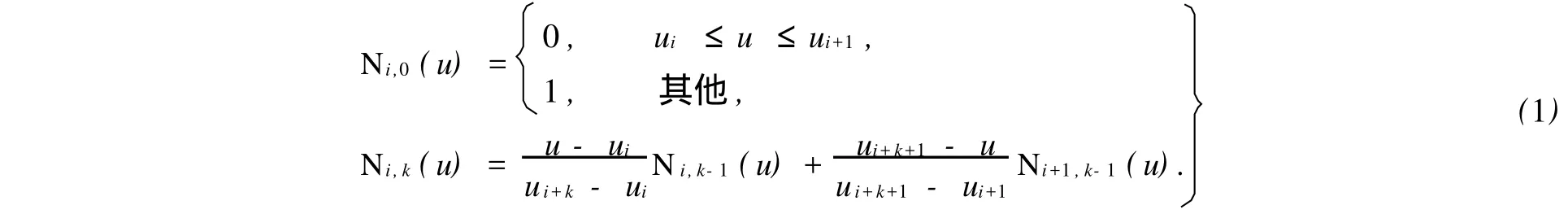
u0=u1=…=uk,un+1=un+2=…=un+k+1.
在大多数实际应用里,端节点值分别取为0与1,因此有曲线定义域u∈[uk,un+1]=[0,1].给定一组有序数据点qi(i=0,1,…,n),要求构造一条NURBS曲线,顺序通过这些数据点,也就是要从给定的数据点,求出定义该NURBS曲线的控制顶点,进而拟合加工出NURBS曲线.
2 3次NURBS曲线拟合
2.1 参数值的计算
同一组型值点,即使采用同样的插值(逼近)法,若选择不同的参数化方法[3],将得到不同的插值(逼近)曲线.型值点的参数化应尽可能反映被插值(逼近)曲线的性质,或设计员欲用型值点所构造的曲线的性质.对型值点的基本参数化方法,主要有均匀参数化、积累弦长参数化、向心参数化等.
均匀参数化就是使每个节点区间长度是一个常数,即节点在参数轴上呈等距分布.这种参数化方法仅适合于型值点多边形各边(弦长)接近相等的场合.当相邻段弦长相差悬殊的情况下,生成插值曲线后,弦长较长的那一段曲线显得较扁平,弦长较短的那段曲线则容易出现尖点或自交.积累弦长参数化法,可以反映数据点按弦长的分布情况,适用于构造的任意k次非均匀有理B样条曲线节点矢量,即参数的计算适合于工程实践的应用.
假定一条k次NURBS曲线通过的数据点为qi(i=0,1,…,n),其参数值的计算为
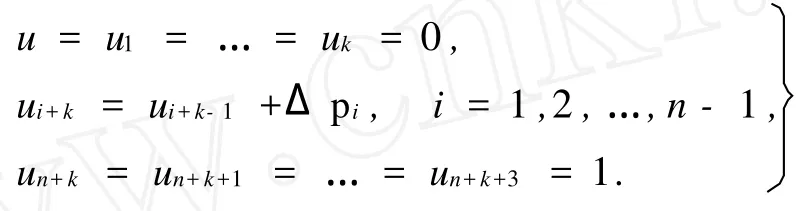
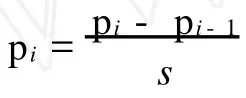
对于3次NURBS曲线,则有
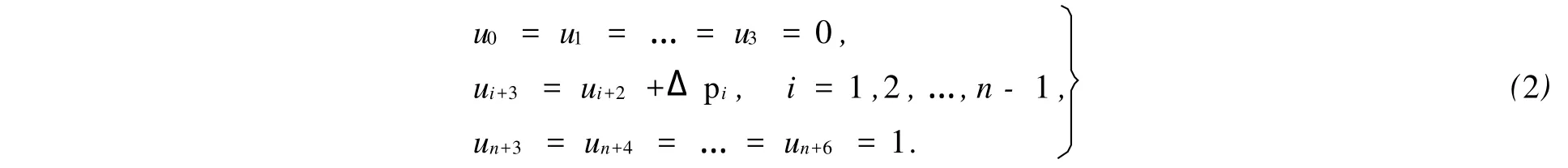
由此可准确算出每一个参数值,并得到其节点矢量U,以便继续后面的运算.
2.2 控制顶点的定义
一条NURBS曲线通过一组给定的数据点qi(i=0,1,…,n),要使其首、末端点分别与首、末数据点一致.即曲线的分段连接点依次与曲线定义域内的节点一一对应[4],qi点有节点值uk+i(i=0,1,…,n).该NURBS曲线由n+2个控制顶点di(i=0,1,…,n+2)与节点矢量U=[u0,u1,…,un+6]来定义,即控制顶点数目要比数据点数目多2个,共有n+2个未知顶点.对于一条通过数据点qi(i=0,1,…,n)的3次NURBS曲线(k=3),其节点值为u3+i(i=0,1,…,n),节点矢量为U=[u0,u1,…,un+6],对应的控制顶点为di(i=0,1,…,n+2).
2.3 3次B样条基的计算
对于周期3次NURBS曲线,首、末数据点q0=qn.由于数据点是作为NURBS曲线的分段连接点,因此由NURBS曲线的性质可知,这些数据点仅由其前后相邻的3个带权控制顶点决定[5].
设带权控制顶点为di(i=0,1,…,n+2).其中:每一个di都是用齐次坐标表示,而带权数据点qi,i=0,1,…,n亦转化为齐次坐标表示.它们之间关系为
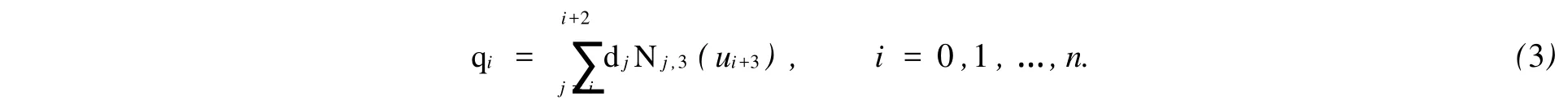
由上述NURBS曲线基本理论可知,Ni,3(u)叫做3次规范B样条基函数,是由节点矢量U=[u0,u1,…,un+6]按德布尔-考克斯递推公式决定的,即式(1).
对于3次NURBS开曲线,常将两端节点的重复度取为4,即
u0=u1=…=u3,un+3=un+4=…=un+6.
在大多数实际应用里,端节点值分别取为0与1.因此,有曲线定义域u∈[u3,un+3]=[0,1].于是,3次NURBS曲线有
u0=u1=…=u3=0,un+3=un+4=…=un+6=1.
当u∈[ui,ui+1],u=ui,i=0,1,2,…,n时,只有Ni+3,0(u)=1,其余均为0.这样就将B样条基中所有包含分母为0的项全部去掉了.经整理,其公式为

2.4 控制顶点的计算
式(1)共含n+1个方程,对于C2连续的3次NURBS闭曲线,因首、末数据点相重,q0=qn,不计重复,方程数减少1个,剩下n个.又由于首、末3个控制顶点依次相重[7],即dn=d0,dn+1=d1,dn+2=d2,则未知控制顶点数少了3个,也剩下了n个.因此,可从n个方程构成的线性方程组中求解出n个未知控制顶点.
将上述计算的3次B样条基的结果代入,得到求解带权控制顶点的矩阵表达式为
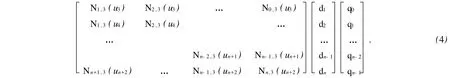
式(4)中:系数矩阵中的元素均为B样条基函数的值,只与节点值有关,采用更直接方便的矩阵形式,有
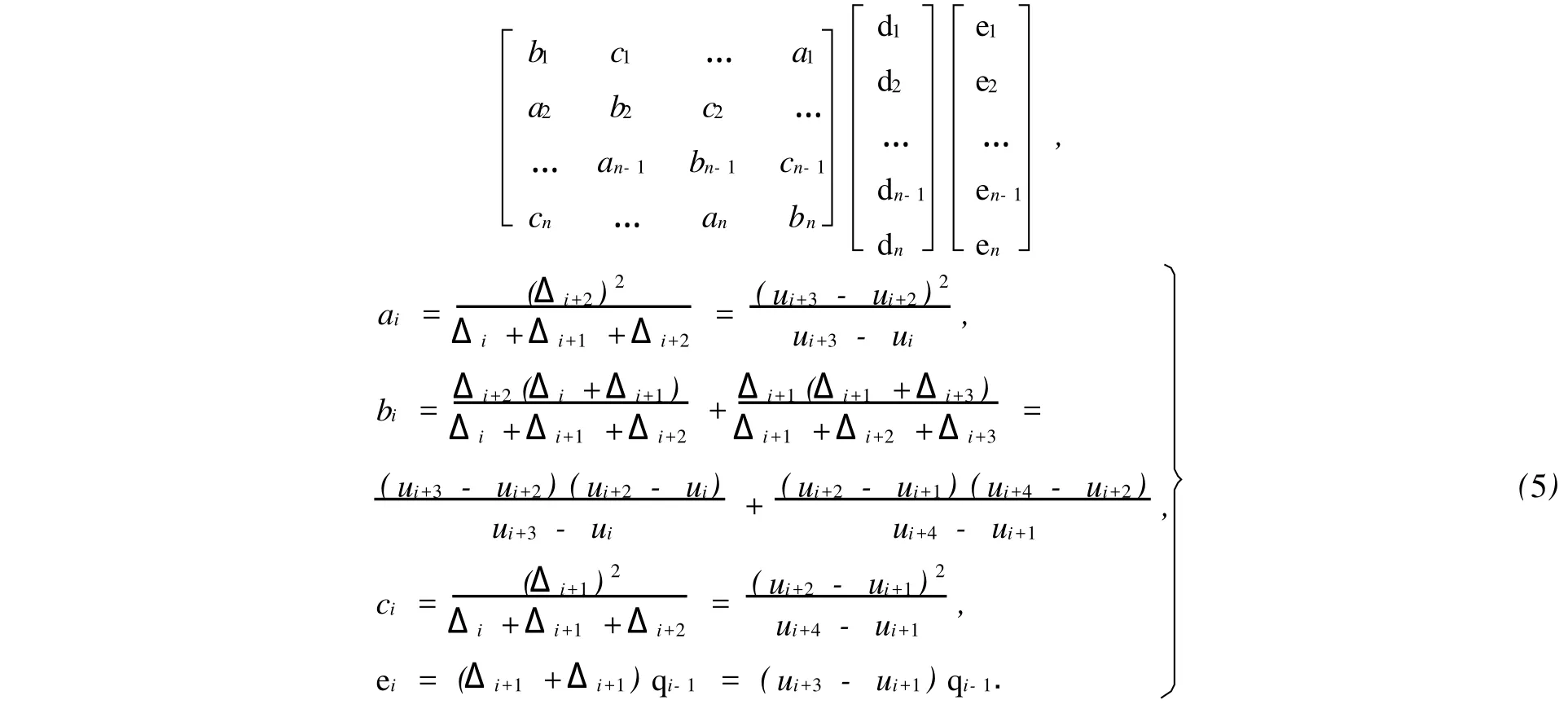
由此,可求出全部未知控制顶点.
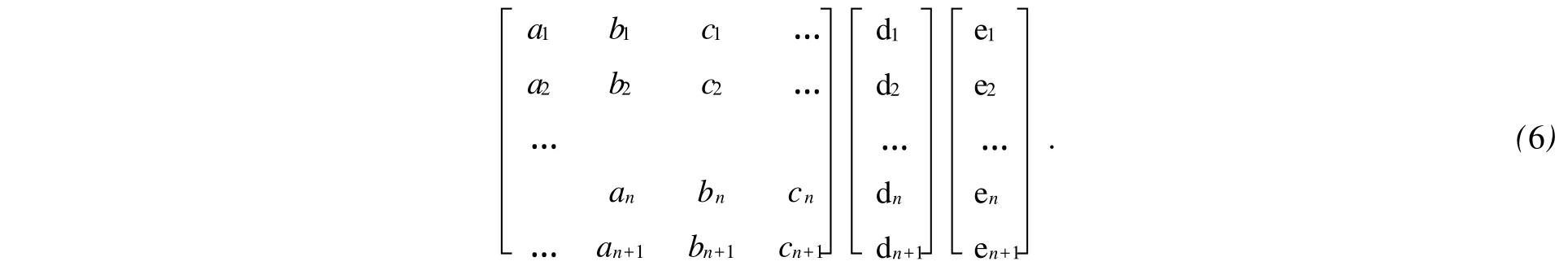
对于3次NURBS开曲线,以及不要求在相重的首、末数据点q0=qn处C2连续的闭曲线,方程组(2)中的n+1个方程,不足以解决其中包含的n+3个未知控制顶点,还必须增加2个通常有边界条件给定的附加方程.这时,求解拟合曲线未知控制顶点的线性方程组,可写成矩阵形式,有式(6)中:系数矩阵中首行非零元素a1,b1,c1与右端列阵中矢量e1表示了首端点边界条件;系数矩阵中末行非零元素an+1,bn+1,cn+1与右端列阵中矢量en+1表示了末端点边界条件;其余各行元素ai,bi,ci(i=2,3,…,n)与闭曲线情况相同.较为常用的是切矢边界条件[8],即节点矢量两端为4重节点和给定曲线两端端点条件.
当取首、末端节点重复度为4时,在四维空间中3次NURBS曲线首、末控制顶点就是首、末数据点,即d0=q0,dn+2=qn,且曲线在首、末端点处分别有切矢,即
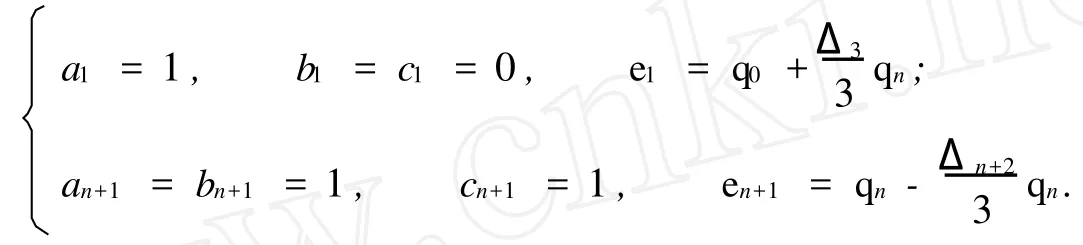
其中:q0与qn分别为给定的首、末数据点q0与qn处的切矢,即端点切矢;其余元素的值同式(5).
由节点矢量可求出系数矩阵,代入式(6),即可求出全部未知控制顶点.
2.5 3次NURBS曲线拟合流程图
在3次NURBS曲线拟合的过程中,首先根据已知的型值点,采用积累弦长参数化化法求出各个参数值;然后,求得节点矢量.根据节点矢量的节点集分别计算B样条基函数,带入带权控制顶点矩阵,求解线性方程组.最后,经计算可得到所有的控制顶点,并拟合出曲线.这个功能可以很方便的用C++语言编程实现,插补流程图,如图1所示.
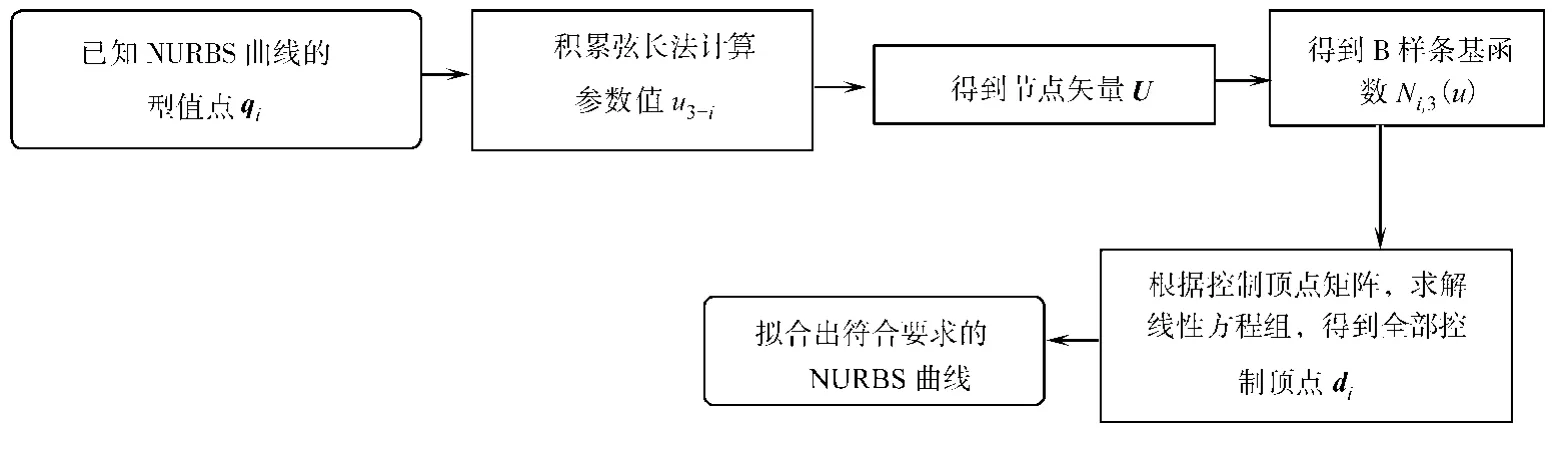
图1 3次NURBS曲线拟合流程图Fig.1 Flow chart of third-order NURBS curve fitting
3 NURBS曲线拟合实例
设qk={(-80,-60),(-40,20),(-20,10),(-10,20),(30,-20),(50,40),(70,30)},采用3次曲线来重构qk.其分段弦长分别是

则总弦长是266.所以,有节点矢量的值为
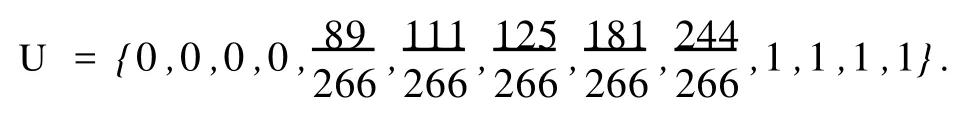
将节点矢量代入线性方程组,再结合式(5),可算出全部控制顶点,所拟合出的曲线,如图2所示.
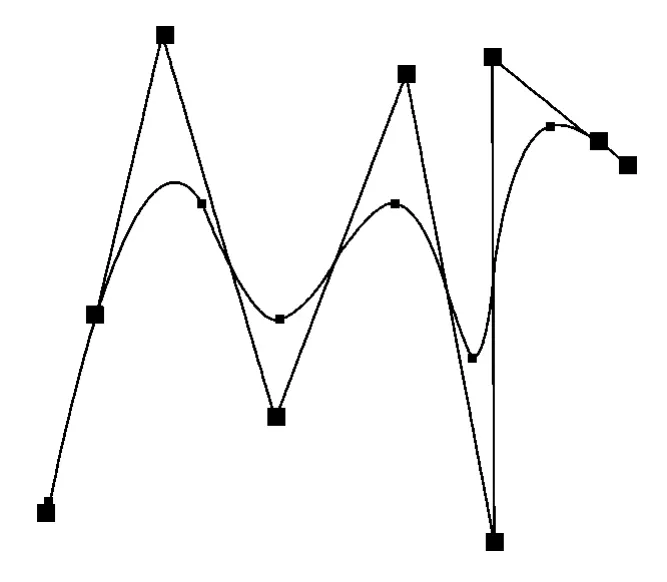
图2 3次NURBS曲线拟合Fig.2 Third-order NURBS curve fitting
4 结束语
在反算控制点过程中,用的参数化方法不同,最后的结果也有差别.所以,在实际应用中要根据数据点的分布情况,选择合适的参数化方法来反算控制点.比较而言,采用积累弦长参数化法最合适.积累弦长参数化法如实反映了数据点按弦长的分布情况,克服了数据点按弦长分布不均匀情况下采用均匀参数化所出现的问题,一直被认为是最佳参数化法,拟合出的NURBS曲线符合要求.
[1]朱心雄.自由曲线曲面造型技术[M].北京:科学出版社,2000.
[2]施法中.计算机辅助几何设计与非均匀有理B样条[M].北京:高等教育出版社,2001.
[3]BRADLEY C,VICKERS G W.Automated rapid prototyping utilizing laser scanning and free-form machining[J].CIRP Annals,1992,41(2):37-40.
[4]吕丹,童创明,邓发升,等.3次NURBS曲线控制点的计算[J].弹箭与制导学报,2006,26(4):357-359.
[5]ZHANG Ying-jie,LIU Shang-ning.Feature extraction from slice data for reverse engineering[J].Frontiers of Mechanical Engineering,2007,2(1):25-31.
[6]韩庆瑶,赵保亚,谭建鑫,等.NURBS曲线曲面重构的方法[J].机械设计与制造,2006,3(3):137-139.
[7]SHAMSUDDIN S M,AHMEDL M A,SAMIAN Y.NURBS skinning surface for ship hull design based on new parameterization method[J].The International Journal of Advanced Manufacturing Technology,2006,28(9):936-941.
[8]YEH Syh-Shiuh,SU Hsin-Chuan.Implementation of online NURBS curve fitting process on CNC machines[J].The International Journal of Advanced Manufacturing Technology,2009,40(5/6):531-540.
Third-Order Non-Uniform Rational B-Spline Curve Fitting Based on Method of Accumulating Chord Length
YE Li,XIE Ming-hong
(College of Mechanical Engineering and Automation,Huaqiao University,Quanzhou 362021,China)
According to a given set of data points of the third-order non-uniform rational B-spline(NURBS)curve,the parametrization method of accumulating chord length which is more effective is used to construct the knot vectors to obtain the B-spline basis.All of the control points are calculated using the matrix of the control points with powers to fit the required curve finally.The final result reveals that data distribution according to the chord length can be shown by this method.This method can be used in parameter calculation during construction of the knot vector of any order NURBS curve,and can be better fit for engineering practice.
non-uniform rational B-spline;accumulating chord length;parameterization;data point;control points;curve fitting
TB 115;TP 391.7
A
1000-5013(2010)04-0383-05
(责任编辑:陈志贤 英文审校:郑亚青)
2008-12-12
谢明红(1968-),男,研究员,主要从事于数控技术、CAD/CAM及计算机视觉的研究.E-mail:xmh3721@tom.com.
福建省自然科学基金计划资助项目(E0640007)
