SRC柱-RC梁混合节点非线性有限元分析

朱奇云，郭子雄

（华侨大学土木工程学院，福建 泉州 362021）

SRC柱-RC梁混合节点非线性有限元分析

朱奇云，郭子雄

（华侨大学土木工程学院，福建 泉州 362021）

在SRC柱-RC梁混合节点试验的基础上，采用通用有限元分析软件Ansys，建立考虑材料非线性的有限元分析模型.在单调加载作用下，对6个SRC柱-RC梁混合节点进行非线性数值模拟.改变梁纵筋配筋率和节点核心区配箍率，通过对荷载-位移曲线的分析，并与试验结果的对比，研究强节点系数对SRC柱-RC梁混合节点的破坏形式、承载力、延性等影响.结果表明，有限元模拟得到的荷载-位移曲线与试验结果吻合较好，从而验证采用有限元数值模拟开展SRC柱-RC梁混合节点研究的可行性.

SRC柱-RC梁混合节点；强节点系数；非线性；有限元分析

型钢混凝土（SRC）组合结构是今后多高层建筑应用的主要结构形式之一.由于钢筋混凝土造价较低，SRC柱和RC梁的组合形式较适合在我国的工程实践中推广应用.目前，对SRC柱-RC梁混合节点的研究主要采用试验手段，有限元分析较少.在试验研究的基础上，借助有限元数值模拟，可为试验研究提供佐证，补充和丰富试验研究结果.由于型钢混凝土节点的复杂性，对型钢混凝土结构的数值模拟主要集中在型钢混凝土梁［1］、型钢混凝土柱［2］等单个构件的研究，所以有必要开展SRC柱-RC梁混合节点的有限元数值模拟研究.本文以SRC柱-RC梁混合节点为研究对象，以Ansys软件为有限元分析手段，对6个SRC柱-RC梁混合节点进行非线性数值模拟.

1 试验概况

1.1 试验设计

6个SRC柱-RC梁混合节点［3-4］柱反弯点之间距离为1.8m，梁反弯点之间距离为2.4m，柱截面尺寸均为250mm×250mm，柱型钢均采用HW125mm×125mm×6.5mm×9mm（Q235），截面纵筋均为4Φ12mm，箍筋φ6@100.试件SRCJ1～SRCJ4的梁截面尺寸为200mm×250mm，梁截面配箍φ6＠100；试件SRCJ5～SRCJ6的梁截面尺寸为250mm×270mm，梁截面配箍φ8@100.梁柱纵筋均采用HRB335钢筋，箍筋采用HPB235钢筋，混凝土强度等级C45.

通过改变梁纵筋配筋率和节点核心区配箍，实现不同的强节点系数.试件参数如表1所示.表1中：ηj为强节点系数，即节点的抗剪承载力与根据节点两侧梁端屈服承载力计算得到的节点剪力的比值；n为柱轴压比.

节点核心区型钢采用柱贯通式，RC梁外侧纵筋连续穿过节点，内侧纵筋在型钢翼缘处截断，与柱型钢翼缘相应位置伸出的连接钢板进行可靠焊接.在柱型钢腹板上连接钢板对应位置设置水平加劲肋传递应力.

试验采用柱端施加水平荷载方式，考虑P-Δ效应.施加水平荷载前，柱顶先由液压千斤顶施加轴向荷载至预定值，并在试验过程中保持恒定；然后，通过MTS电液伺服加载系统施加水平荷载，整个加载过程采用位移控制.各位移幅值在试件屈服前循环1次，在试件屈服后循环3次，直至试件承载力下降至最大荷载的85％停止加载.采用导杆引伸仪量测梁柱塑性铰区域的弯曲变形和节点核心区的剪切变形，采用电阻应变片及应变花重点量测梁端纵筋、节点核心区箍筋和型钢腹板的应变.

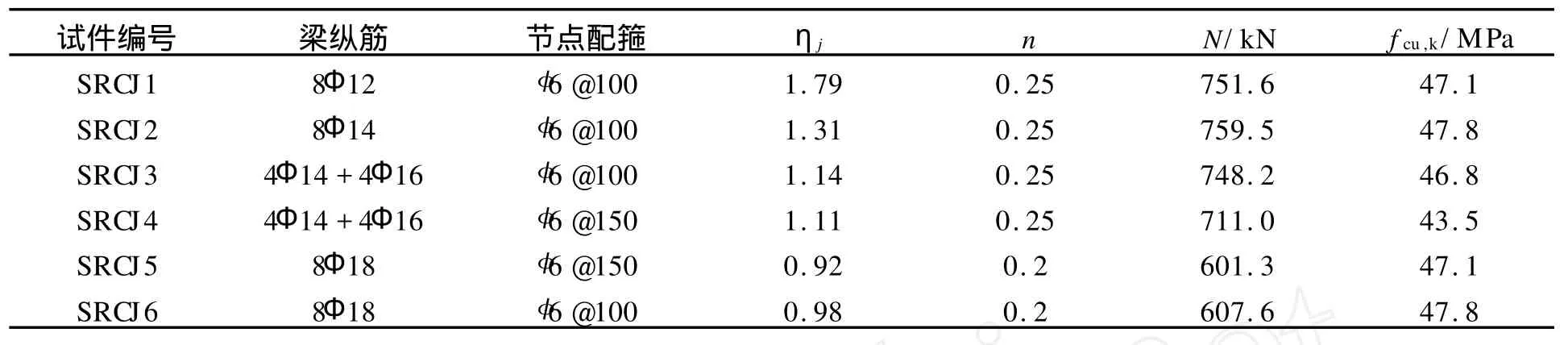
表1 试件参数Tab.1 Parameters of specimens

1.2 主要试验现象

对于强节点系数较大的试件SRCJ1和SRCJ2，在试验过程中裂缝发展主要集中于梁端，如梁端纵筋屈服、表层混凝土剥落、梁端形成塑性铰，而节点核心区裂缝发展较少，型钢腹板和箍筋应变较小，最终呈现“梁端弯剪”的破坏形态，如图1（a）所示.

试件SRCJ3和SRCJ4在加载过程中梁端出现弯曲裂缝和斜向剪切裂缝，同时节点核心区出现交叉斜裂缝，型钢腹板主拉方向达到屈服，破坏从梁端转向节点核心区，呈现"梁端弯剪-节点剪切"的破坏形态，如图1（b）所示.

强节点系数较小的试件SRCJ5和SRCJ6在试验过程中主要在节点核心区形成X型剪切裂缝，且梁端与节点核心区接触面产生粘结滑移裂缝.核心区型钢腹板与箍筋均达到屈服后，节点剪切破坏迅速加剧，导致核心区混凝土剥落，试件以节点剪切破坏为主，如图1（c）所示.

综上所述，强节点系数是影响SRC柱-RC梁节点破坏形态的主要因素.

图1 破坏形态Fig.1 Failure modes

2 有限元模型

2.1 参数定义

2.1.1 混凝土 混凝土采用Solid 65单元，实常数中的配筋率均取0，其材料性质如表2所示.表2中：E0为混凝土弹性模量；f′c，ft分别为单轴抗压强度和单轴抗拉强度；混凝土的泊松比为0.2；张开裂缝的剪力传递系数βt为0.35；闭合裂缝的剪力传递系数βc为0.9.

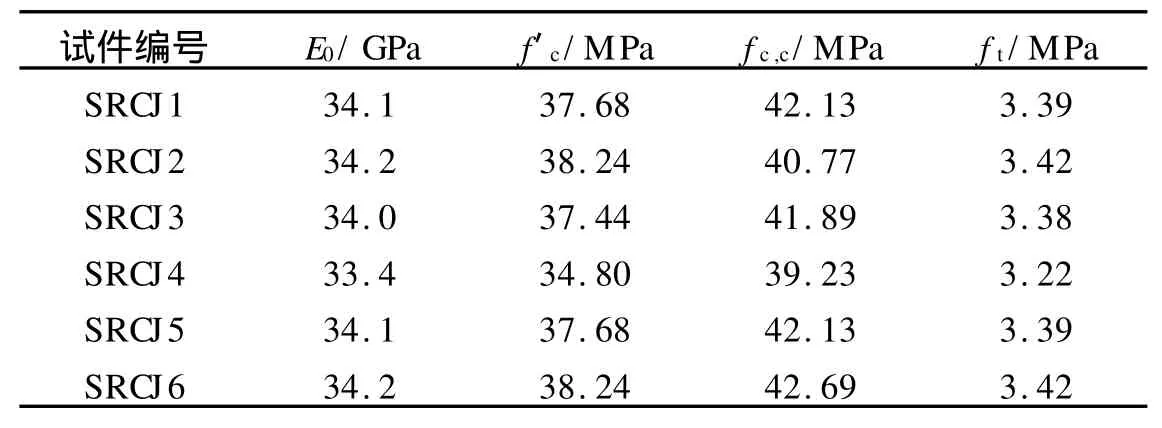
表2 混凝土的材料性质Tab.2 Material properties of concrete

在Ansys分析中，混凝土破坏采用William-Warnke五参数破坏准则，混凝土材料本构关系按非线性弹性材料模型（MELAS）输入.将SRC柱截面混凝土划分为两个区，如图2所示.箍筋外的保护层混凝土视为近似无约束区；考虑到箍筋和型钢对混凝土的约束作用，箍筋内的混凝土视为约束区.

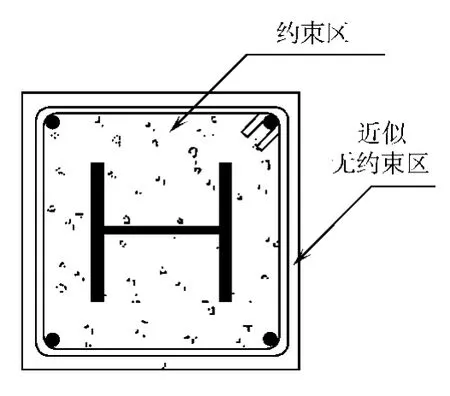
图2 截面划分Fig.2 Section division

选取Saenz模型模拟箍筋外无约束区混凝土单轴受压应力-应变关系.箍筋内的混凝土处于多轴受力状态，可等效为单轴受压应力状态，故采用Priestley等［5］改进的Mander［6-7］约束混凝土模型.即

2.1.2 钢材 型钢和支座处弹性垫块采用无需设置实常数的Solid 45单元；纵筋和箍筋均采用Link 8单元模拟，根据钢筋的面积输入实常数.型钢、纵筋和箍筋采用多线性随动强化模型（MKIN），钢材单轴应力状态下应力-应变曲线按考虑硬化的三折线模型输入.钢材的弹性模量根据规范取值，泊松比取0.3，钢材的屈服强度和极限强度均采用材性试验实测值，强化段的斜率取0.05Es.钢材的材料性质，如表3所示.

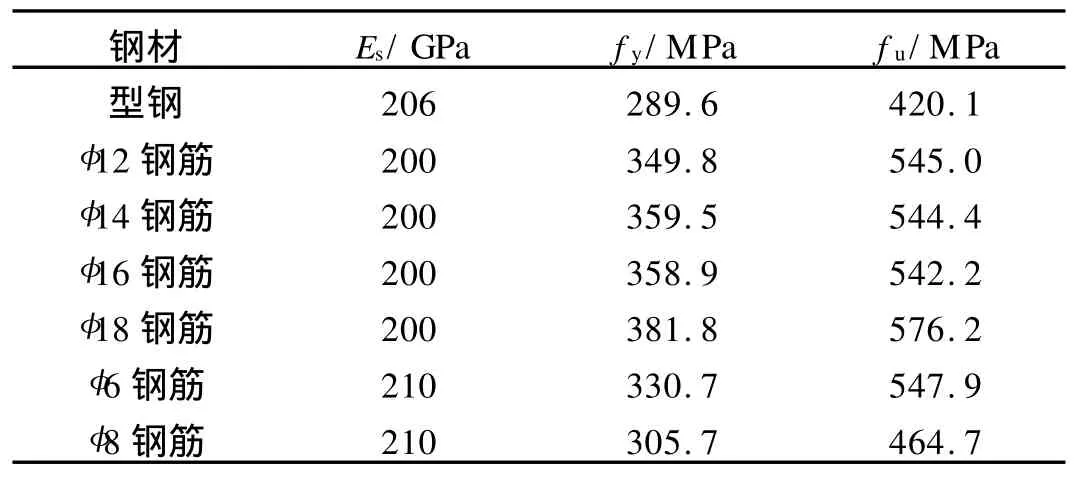
表3 钢材的材料性质Tab.3 Material properties of steel

2.2 模型建立

不考虑型钢、钢筋与混凝土之间的粘结滑移，采用实体建模方法.首先根据梁柱混合节点的几何尺寸生成梁与柱的块体，运用布尔操作将几个实体胶合成整体.然后，在型钢翼缘、腹板、加劲肋、钢筋等关键位置处，用工作平面切分实体模型.最后，为型钢和混凝土块体赋予相应的材料属性，选择合理的网格密度对实体模型进行六面体单元映射网格划分，以实现计算效率和精度的平衡.

选择梁柱钢筋所在位置的线，根据型钢、混凝土单元的大小划分网格，生成钢筋单元.钢筋与混凝土单元共用节点，建立的有限元模型如图3所示.采用APDL参数化命令程序编写命令流，通过在命令流中改变试件研究参数，能方便地实现不同研究参数试件的Ansys有限元数值模拟.

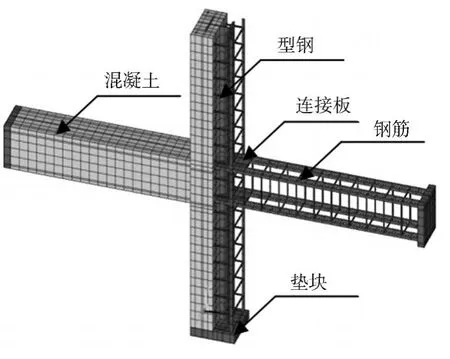
图3 有限元模型Fig.3 Finite element model

2.3 加载求解

根据试验中试件的实际约束边界，柱底通过连接板与球铰支座紧固连接，梁端与铰接连杆上端通过连接件铰接，以模拟梁柱反弯点处的铰接.如果直接在柱底中部一排节点上约束3个平动自由度，会导致应力集中.将柱底所有节点约束3个平动自由度，不能真实地反映柱底铰接.因此，在柱底设置弹性垫块，约束垫块中间一排节点的3个平动自由度.同理，在左右梁端均设置弹性垫块，约束Y，Z向平动自由度.

加载过程分两个荷载步.第一荷载步在柱顶施加恒定的轴向压力.轴压力通过对柱顶截面施加均匀面压力模拟.采用此加载形式与试验过程轴向压力加载方式相同，轴向荷载始终垂直柱顶平面.

第二荷载步施加柱顶位移.考虑到水平荷载直接施加在柱头节点可能会引起局部应力集中，且运算不收敛.因此在第二荷载步水平位移施加前，先对柱顶所有节点耦合水平加载方向的平动自由度；然后，对耦合后的主节点施加位移.这种加载形式能够很好地避免应力集中.为使运算更好地收敛，打开自动时间步长、线性搜索和自由度预测.

3 计算结果分析

在Ansys中输入APDL参数化设计语言编制的命令流，提取柱底节点的总反力和柱顶位移值，形成Ansys数值模拟的荷载-位移曲线.将其与试验结果骨架曲线对比，结果如图4所示.

从图4可以看出，6个试件的Ansys有限元分析得到的荷载-位移曲线与试验的骨架曲线总体吻合较好，与试验结果表现出一致的规律.

图4 数值计算与试验结果对比Fig.4 Comparison between calculation and test results

根据荷载-位移曲线计算所得的主要特征点值，如表4所示.表4中：e为误差值.为了与试验结果相比，极限位移取水平荷载下降至最大荷载85％的点所对应的位移值；而屈服荷载、屈服位移则由能量等值法确定.

表4 特征点计算结果与试验结果对比Tab.4 Comparison between calculation and test results at characteristic points

从表4可以看出，Ansys有限元计算所得的屈服荷载和最大荷载与试验结果相比较为接近，两者相对误差在10％以内.但是，极限位移小于试验结果.这主要是由于试验加载后期，梁纵筋在节点核心区滑移引起附加的柱端位移，而有限元计算中未考虑梁纵筋与混凝土之间的滑移，致使有限元计算所得的极限位移偏小.

对于强节点系数较大的试件SRCJ1和SRCJ2，以梁端弯曲破坏为主，节点承载力与梁端纵筋配筋率有关.对比SRCJ3和SRCJ4，SRCJ5和SRCJ6的曲线，核心区配箍率较小的试件下降段相对较陡，节点核心区的箍筋配置对试件强度影响不大，对试件后期延性有一定影响，而且对于强节点系数较小的试件影响尤为显著.

4 结束语

采用的数值模拟技术，可较好地实现Ansys有限元软件对SRC柱-RC梁混合节点从加载到屈服，直至达到极限的全过程分析.通过对不同强节点系数的SRC柱-RC梁混合节点在单调加载作用下的非线性有限元模拟表明，有限元分析结果与试验结果吻合较好.梁纵筋在节点核心区内的粘结滑移对SRC柱-RC梁混合节点变形的影响不可忽略，建议在今后的节点数值模拟过程中，应考虑梁纵筋在节点核心区混凝土内的粘结滑移.

［1］杨勇，郭子雄，聂建国，等.型钢混凝土结构Ansys数值模拟技术研究［J］.工程力学，2006，23（4）：79-85.

［2］王妙芳，郭子雄.型钢混凝土柱的Ansys数值模拟技术［J］.华侨大学学报：自然科学版，2009，30（2）：195-199.

［3］庄云.SRC柱-RC梁混合节点抗震性能试验研究［D］.泉州：华侨大学，2007.

［4］刘轩.SRC柱-RC梁节点抗剪性能及节点加固试验研究［D］.泉州：华侨大学，2008.

［5］PAULAY T，PRIESTL Y M J N.Seismic design of reinforced concrete and masonry muildings［R］.NewYork：John Wiley＆Sons Inc，1992.

［6］MANDER J B，PRIESTL EY M J N，PARK R.Theoretical stress-strain model for confined concrete［J］.Journal of Structural Engineering，1988，114（8）：1804-1826.

［7］MANDER J B，PRIESTL EY M J N，PARK R.Observed stress strain behavior of confined concrete［J］.Journal of Structural Engineering，1988，114（8）：1827-1849.

Nonlinear Finite Element Analysis of SRC Column-RC Beam Hybrid Joints

ZHU Qi-yun，GUO Zi-xiong
（College of Civil Engineering，Huaqiao University，Quanzhou 362021，China）

Based on the experimental results of steel reinforced concrete（SRC）column-RC beam hybrid joints，the finite element model considering material nonlinear is established by Ansys software.Nonlinear numerical simulation of six SRC column-RC beam hybrid joints under the monotonic loading is carried out.According to the analysis of load-displacement curves and comparison with experimental results，the influence of strength ratio of joint to beam on the failure modes，strength and ductility of specimens is investigated for different longitudinal reinforcement ratios of beam and stirrup ratios of joint core.The analysis results indicate that the load-displacement curves of six specimens are in good agreement with the experimental results，so the finite element numerical simulation of SRC column-RC beam hybrid joints is feasible.

SRC column-RC beam hybrid joints；strength ratio of joint to beam；nonlinear；finite element analysis

TU 375.102

A

1000-5013（2010）04-0453-05

（责任编辑：钱筠 英文审校：方德平）

2009-12-10

郭子雄（1967-），男，教授，主要从事工程结构抗震的研究.E-mail：guozxcy@hqu.edu.cn.

国家自然科学基金资助项目（50978107）；福建省自然科学基金资助项目（E0810021）；厦门市科技计划项目（3502Z20093029）