复杂系统风险分析的模拟方法

王敬，王全凤

（1.中冶建筑研究总院有限公司，北京 100088；2.华侨大学土木工程学院，福建 泉州 362021）

复杂系统风险分析的模拟方法

王敬1，王全凤2

（1.中冶建筑研究总院有限公司，北京 100088；2.华侨大学土木工程学院，福建 泉州 362021）

采用粗糙集理论进行知识约简并选择主要风险因素，应用神经网络理论方法寻找主要风险因素与总体风险之间的模糊关系模型.最后，采用蒙特卡罗方法模拟系统总体风险的概率分布，形成复杂系统风险分析的集成模拟方法.通过水利生态系统实例验证，证明该方法是合理且可行的.

知识约简；粗糙集；风险分析；神经网络；蒙特卡罗仿真

对复杂系统的风险分析，主要是解决以下3个方面的问题：（1）风险因素的辨识及主要风险因素的确定；（2）如何根据主要风险因素的水平来表达系统整体风险的水平，即整体风险的评估；（3）如何寻找系统风险的概率分布，对风险的重要性作出判断.近年来，我国已经实施或者正在规划一系列流域生态环境恢复水资源保障计划.对水利生态系统分析的目标，就是寻求系统的最优发展路径.这个目标具有一定的模糊性和不确定性，无法用简单的函数表达.水利生态系统初始状态向目标状态转移的路径集合中，各条路径成为最优路径概率不同，因此需要将不同路径的风险水平引入系统可持续发展测度的计算中.即将研究目标转化为评估系统不同发展路径的风险水平，并以此进行水利生态系统的可持续状态分析.本文通过近代数学方法，对水利生态复杂多样的系统进行风险分析.

1 基于知识约简的风险因素分析

粗糙集是一种处理不精确、不确定与不完全数据的新的数学理论［1-5］.知识约简是粗糙集理论的核心内容之一.通过知识简约可以在复杂、繁多、变化的知识库中进行知识挖掘，寻找并确定解决问题所需的充分必要的条件（因素），为解决问题提供基础依据.文中所研究的问题为完备信息系统，因此，只讨论完备信息系统的知识约简问题.

1.1 完备信息系统的知识约简［2］

定义1 设S=（U，A，F）是一个信息系统，其中U为对象集，A为属性集，A=｛a1，a2，…，am｝，F为U与A之间的关系集，即F=｛fl∶U→Vl｝，其中Vl为al（l≤m）的值域.

定义2 设S=（U，A，F），至少存在一个α∈A T，使得Vl含有空值，则称知识表达系统S为不完备信息系统；否则，称S为完备信息系统.

对于完备信息系统，通过建立区分矩阵来计算区分函数，由区分函数的值确定信息系统的约简与核，从而实现信息系统的知识约简.

（1）区分矩阵与区分函数.

定义3 设S=（U，A，F），则区分矩阵是一个n×n的对称矩阵，矩阵中的任意元素为

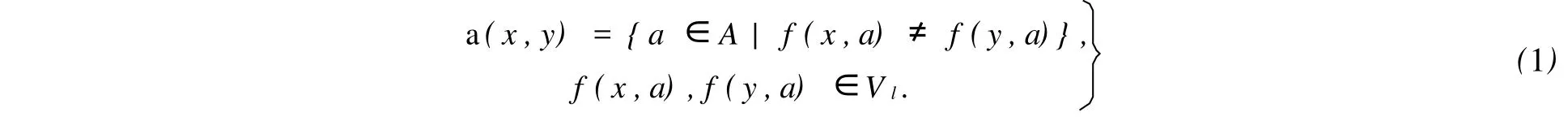
定义4对每一个属性a指定一个布尔变量α，若α（x，y）=｛α1，α2，…，αk｝≠Φ，则令α（x，y）=1.区分函数可定义为

（2）约简与核.区分函数Δ的极小析取范式中，所有合取式是属性集A的所有约简.核是区分矩阵中所有单个元素组成的集合，即

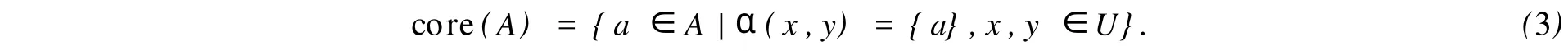
定理1 定义red（A）为A的所有约简，由此可得核与约简的关系为

core（A）=∩red（A）.

1.2 知识约简步骤

在整个模型的运行过程中，存在着以下不同环节的风险.这些环节包括［6］：（1）制度设计与执行环节；（2）水利-生态系统供需水量优化配置环节；（3）社会-生态-经济绩效及发展状态分析环节.

这些环节涉及自然、社会、经济、工程、管理等多种因素，汇集所有的风险因素，就构成了水利生态系统的风险因素集.这些因素主要包括以下16项：（1）可调用水量，包括来水的不确定性因素；（2）水利生态工程对径流的控制能力；（3）水库对生态供水的调控能力；（4）水土流失风险；（5）法律、法规风险因素；（6）生态系统需水量；（7）水利生态绩效分析方法的科学性；（8）生态用水价格变化；（9）各相关部门的协调管理风险因素；（10）水利生态系统运行所需资金的筹措和使用风险；（11）社会道德风险.（12）人口总量及增幅对生态系统的消耗；（13）牲畜总量及增幅对生态系统的消耗；（14）生态水权的定位和执行风险；（15）生态系统服务功能价值计算体系的完善程度；（16）跨流域调水量，即对于使用跨流域调水量需要考虑跨流域调入水量存在的风险.

对于不同的水利生态系统，以上风险因素根据具体情况有所不同，应该按照实际情况考虑.文中的案例没有跨流域调水量，因此，去掉需要考虑跨流域调入水量存在的风险，则确定该水利生态系统的风险由其余的15个评价指标构成.即A=｛a1，a2，…，a15｝.按照风险因素对系统目标的影响程度，取风险评语集为V=｛很大，大，中，小｝，并按照上述理论进行知识约简.

按照该水利生态系统的具体情况，根据不同的来水频率（η）、调水方案（A：水源独立供水；B：水源独立供水；A+B：水源联合调度）、生态补水路线（3条）、生态水权状态、生态需水量（V）大小等，可形成多种运行方案.选取其中9个方案进行分析，U=｛x1，x2，…，x9｝，如表1所示.

表1 方案简表Tab.1 Projects

通过专家调查、打分，获得各个方案风险因素的评语集，如表2所示.为说明问题及节省篇幅，以下取x1，x2，x3方案进行详细分析.

表2 方案与风险因素关系表Tab.2 Relationship between project and risk factor

（1）依据给定的关系表，计算区分矩阵中各元素的值，列出区分矩阵为

由区分矩阵，计算区分函数，有

（2）根据区分函数的值，找出信息系统的所有约简为｛a1｝，｛a6｝，｛a9｝，｛a10｝，｛a11｝，｛a14｝，｛a15｝.

（3）从信息系统所有约简中，按照找出信息系统的核.由于从所有信息系统的约简中找不出核，所以约简后信息系统的属性取为a1，a6，a9，a10，a11，a14，a15.

（4）根据定义，按照核或约简中包含的元素，列出约简后的关系表（限于篇幅，略去）.

通过9个方案约简后，最终属性集合变为A=｛a1，a6，a9，a10，a11，a14｝，即该属性集合中的元素是主要风险因素.

2 风险估计的神经网络模型

主要风险因素确定后，即可建立其与整体风险水平的关系.采用风险效用来表示系统的整体风险［7］.风险效用是指对主要风险因素所导致系统可能偏离目标程度的判断.如果用U表示风险效用，用Z=（z1，z2，…，zn）表示主要风险因素，则两者之间的关系为

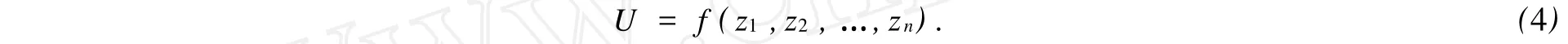
一般情况下，由于项目的复杂性，以及各种因素的相互作用等影响，主要风险因素与项目总体风险之间并不能直接用数学表达式（函数式）表达，即f一般无法得到具体的关系.为了形成一种具有普遍意义的方法，采用神经网络方法建立主要风险因素与风险效用之间的关系.

2.1 主要风险因素标准化与概率分析

2.1.1 主要风险因素量化 因素属性分为效益型、成本型等多种类型.类型不同，对属性值的要求也不相同.为了更好地进行神经网络训练与模拟，对涉及的两种主要风险因素进行标准化分析.

（1）效益型.其量化值计算方法为

（2）成本型.其量化值计算方法为

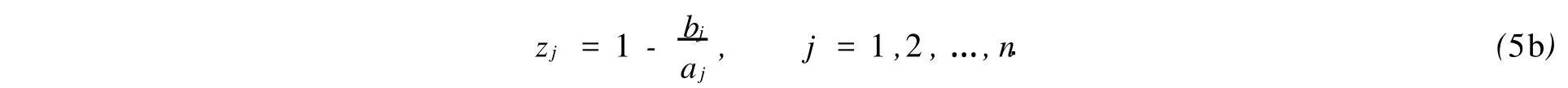
上两式中：Zj，aj分别为风险因素的第j个量化标准值和评估值，n为方案数量；bj=max（aj）或bj=，而为因素的理想点.

2.1.2 主要风险因素的概率分析 确定风险事件的概率分布通常有3种方法［6］，即根据历史资料确定风险事件的概率分布、利用理论概率分布和主观概率法.对于具有长系列资料的因素，通过分析，可直接选用概率统计中的概率分布进行风险估计.当没有足够的资料来确定风险事件概率分布时，可利用理论概率分布或主观估计的方法对其进行估计.

水资源风险估计中常用的概率分布有正态分布、对数分布、皮尔逊Ⅲ型分布等.在获得的信息不够充分的条件下，需要根据主观判断和近似的方法来确定概率分布.由于水利生态实践的时间较短，对风险因素概率的分布研究缺乏足够的统计资料和数据分析成果，因此可以采用推断、主观判断和理论概率分布等方法表达各因素的概率分布.文中风险因素的概率分布主要采用［0，1］均匀分布，如z1，z2，z3，z4，z5，以及［0，1］区间内分段取定值分布，如z6.

2.2 效用-风险因素关系神经网络模拟模型

2.2.1 风险模拟的神经网络结构［8］选择基本的BP网络作为解决实际问题的工具，通过对训练样本的学习、误差反馈、逐渐逼近并形成模型，其结构关系是通过组织输入层与隐含层、隐含层与输出层间的连接关系来实现的.输入层中，神经元个数与主要风险因素个数n相同；输出层中，风险效用U即输出层的神经元个数为1；隐含层神经元的个数尚无统一的确定方法，视具体情况由训练过程确定.

2.2.2 网络学习样本的确定及网络训练

（1）学习样本的输入.经过知识约简后，取可调用水量，生态系统需水量、各相关部门的协调能力、水利生态建设、运行所需资金的筹措和使用风险、社会道德风险生态水权等6个为主要风险因素.将其作为输入向量，经过排序、量化、归一化后，结果如表3所示.

表3 风险因素相对数值Tab.3 Relative values of risk factor

（2）学习样本的输出.根据上述9个方案的主要风险因素的取值，采用专家调查方法，可分别获得9个方案x1～x9的风险效用U：0.305 3，0.523 5，0.911 2，0.813 4，0.751 1，0.755 6，0.278 9，0.356 7，0.400 1.

（3）神经网络收敛结果.以表3及风险效用值为样本，采用Matlab程序库中函数训练的BP网络模型，建立输入层为6个单元，隐含层为2个单元，输出层为1个单元的BP神经网络模型.神经网络训练收敛过程，如图1所示.图1中：T为精度值；n为循环次数.

图1 神经网络训练收敛过程Fig.1 Convergence process of training of neural network

2.3 基于蒙特卡罗模型的风险概率模拟

水利生态可持续发展方案风险分析是多因素多目标风险问题，直接由各主要风险因素的概率分布组合求出风险目标的理论概率分布很困难.这是因为确定各主要风险因素的理论概率分布存在困难；而且对于多因素的联合概率分布的确定就更困难.鉴于此，采用蒙特卡罗模拟技术［9］进行风险目标的概率分布分析.

设效用与主要风险因素之间函数关系如式（4），按照主要风险因素的概率分布，抽取一组随机变量（z1，z2，…，zn）的值，按照训练完成的神经网络模型确定U的值.反复独立抽样（模拟）多次，便可得到函数的一批抽样数据.当模拟次数满足预定的精度要求时，便可给出与实际情况相近的函数U的概率分布及其数字特征，即完成了系统的风险估计.模拟得到的水利生态系统的风险概率分布图，如图2所示.

2.4 系统风险评价

在风险估计的基础上，通过系统风险效用值及系统风险的概率分布对系统的风险状态进行综合分析，可以得到不同方案水利生态系统的风险水平.风险水平可定义为

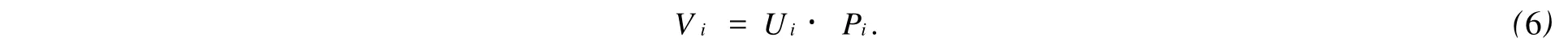
对于给定的方案i，其风险效用值为Ui（由神经网络模型得到），频率为Pi（由图2给出），则该方案的风险水平为Vi.Vi反映了风险的相对严重性.Vi越小说明系统的风险水平越低，系统越可靠；反之亦然.有时风险的效用值Ui很大，但由于出现的概率较低，风险水平并不高；而有时效用值Ui并不大，但由于出现的概率较高，风险水平并不低，系统的可靠性不高.

对于上述案例，通过模拟可得到不同方案风险的相对排序为

V2＞V9＞V8＞V1＞V6＞V5＞V7＞V4＞V3.

说明，方案3的风险水平最低，而方案2的风险水平最高.

3 结束语

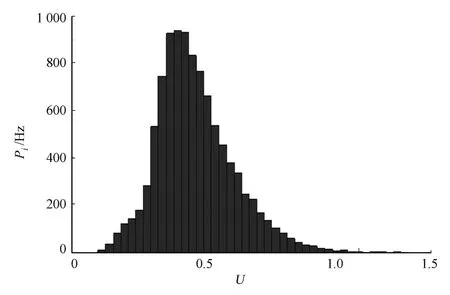
图2 水利生态系统的风险概率分布图Fig.2 Distribution of risk probability for water conservancy ecosystem

复杂系统一般都具有多属性、空间尺度和时间延伸性共同作用，以及在系统运行过程中多环节、多主体的特点，导致对这种系统的风险评价十分复杂.文中以水利生态系统风险分析为例，通过粗糙集理论、神经网络和蒙特卡罗等方法的集成，形成一种基于知识简约、神经网络模型和蒙特卡罗模拟的复杂系统的风险分析方法.水利生态系统风险分析的验证结果表明，通过不同方案风险水平的计算，可直观地比较不同方案的风险影响程度，为复杂系统的风险分析提供一种新方法.

［1］MI Ju-sheng，WU Wei-zhi，ZHANG Wen-xiu.Approaches to knowledge reduction based on variable precision rough set model［J］.Information Sciences，2004，159（3/4）：255-272

［2］张文修，仇国芳.基于粗糙集的不确定决策［M］.北京：清华大学出版社，2005.

［3］YAHIA M E，MAHMOD R，SULAIMAN N.Rough neural expert systems［J］.Expert Systems with Applications，2000，18（2）：87-99.

［4］张文修，吴伟志，梁吉业，等.粗糙集理论与方法北京［M］.北京：科学出版社，2001.

［5］方千山.粗糙集理论在模糊隶属函数辨识中的应用［J］.华侨大学学报：自然科学版，2003，24（1）：33-38.

［6］王敬.水利生态系统可持续发展研究［D］.北京：华北电力大学，2007.

［7］沈建明.项目风险管理［M］.北京：机械工业出版社，2003.

［8］楼顺天，施阳.基于MATLAB的系统分析与设计：神经网络［M］.西安：西安电子科技大学出版社，1999.

［9］LIU J S.科学计算中的蒙特卡罗策略（英文影印版）［M］.北京：世界图书出版社，2005.

Simulation Method for Risk Analysis in Complex System

WANG Jing1，WANG Quan-feng2
（1.Central Research Institute of Building and Construction CO.L TD.MCC Group，Beijing 100088，China；2.College of Civil Engineering，Huaqiao University，Quanzhou 362021，China）

The rough set theory（RST）is used as knowledge reduction and the selection of main risk factors.The fuzzy relationship model between main risk factors and overall risk is established by artificial neural network（ANN）.The probability distribution of overall system risk is simulated by Monte Carlo method，an integrated simulation method is proposed for complex system risk analysis.The method is reasonable and feasible by verification of water conservancy ecosystem.

knowledge reduction；rough set；risk analysis；artificial neural network；Monte Carlo simulation

TV 213.4；TP 18

A

1000-5013（2010）03-0337-05

（责任编辑：黄仲一 英文审校：方德平）

2009-05-05

王全凤（1945-），男，教授，主要从事土木工程的研究.E-mail：qfwang@hqu.edu.cn.

水利部水利生态绩效审计评价基金资助项目（040310）