异步电机三角形接法时空间矢量脉宽调制技术分析
2010-08-28许连丙张爱玲武德祥李天波
许连丙, 张爱玲, 武德祥, 李天波
(1.太原理工大学,山西太原 030024;2.阳城国际发电责任有限公司,山西晋城 048102)
0 引言
在高性能全数字控制的交流伺服驱动系统中,通常采用数字脉宽调制(Pulse Width Modulation,PWM)方法来代替传统的模拟PWM。近年来出现的空间矢量脉宽调制(Space Vector Pulse Width Modulation,SVPWM)技术与传统的正弦脉宽调制(Sin-Wave Pulse Width Modulation,SPWM)技术相比,在直流电压利用率等方面,其存在着明显的优势,因此在电机控制上得到了广泛应用。例如,在异步电机矢量控制系统中,根据需要计算出所需电压的α、β分量后,再用SVPWM技术确定需要施加的基本电压空间矢量,从而确定逆变器的开关状态。但是,SVPWM技术是对电机的相电压进行调制的。分析表明,在异步电机采用Y和△接法两种情况下,逆变器相同的开关状态合成的基本电压空间矢量的大小和相位并不相同,如果不对电机的绕组接法进行判断而采用相同的调制方法,将会导致错误的控制结果。文献[1-5]给出的调制算法均基于电机Y接法,本文分析了△接法情况下,逆变器不同开关状态对应的空间矢量的幅值和相位,以及扇区的划分方法,并与Y接法的情况进行了对比。
1 电机Y接与△接的空间矢量合成
1.1 逆变器的开关状态
图1是典型的三相电压型桥式逆变电路。图中V1~V6是6个全控型开关器件,同一桥臂的开关器件呈相反的开关状态。设上桥臂导通为1,下桥臂导通为0,则逆变器的工作状态共有8种,分别是000,100,110,010,011,001,101,111。其中,000与111使逆变器输出电压为零,称为零矢量,其余6种对应6个基本的电压空间矢量。在绕组采用Y及△接法两种情况下,它们的大小及相位不同,分述如下。
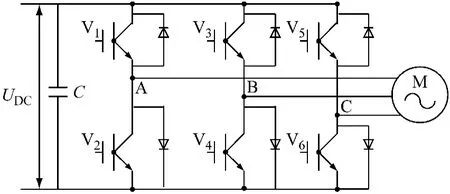
图1 电压型逆变器
1.2 电机绕组Y接法时的电压空间矢量及扇区划分
定义三相电压矢量在各自绕组的轴线上,如图2所示;6个基本电压空间矢量的幅值和相位如表1所示;相位分布及扇区划分如图3所示。
表1 中:Ua、Ub、Uc分别是 A、B、C 三相绕组的相电压(ABC坐标系的数值);Uα、Uβ是各开关状态对应的基本电压矢量分解到αβ坐标系上的分量;Us为合成的基本电压空间矢量的大小,Us相位表示基本电压空间矢量的相位。
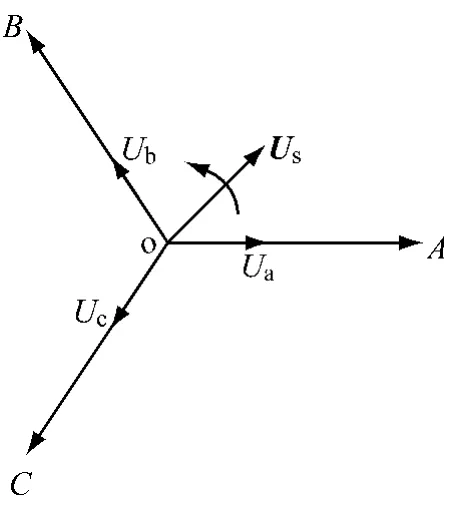
图2 电压空间矢量

表1 星型接法下基本电压空间矢量、各绕组的相电压及其合成矢量αβ坐标轴的分量(功率不变)
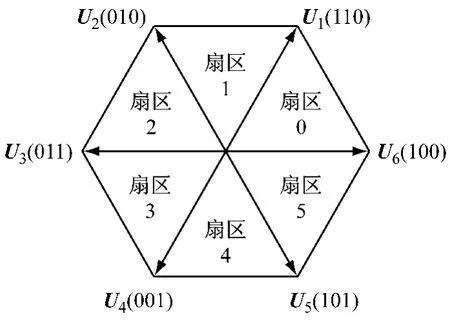
图3 星型接法基本电压空间矢量及扇区划分
1.3 电机绕组△时的电压空间矢量合成及扇区划分
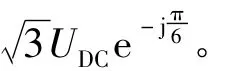
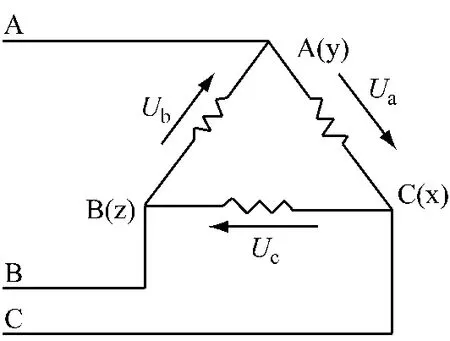
图4 绕组三角形接法
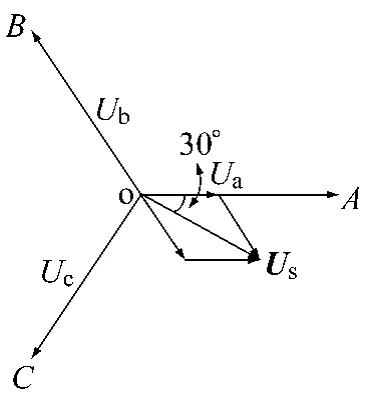
图5 状态100时的向量合成(ABC坐标系)
图6表示的是开关状态为110时空间矢量的大小与相位。按照同样的方法可得其他空间矢量的大小及相位(见表2和图7)。对比图3、7及表1、2可见,两种接法时6个基本电压空间矢量的相位不同,△接法比Y接法时合成的空间矢量相位滞后π/6(逆时针为正方向),并且前者幅值是后者的倍(ABC坐标)。表2给出了不同开关状态对应的相电压(ABC坐标系)及其合成在αβ坐标系的分量(功率不变)。对比表1、2可见,两种接法对应的相电压也不相同。

表2 三角形接法下各绕组的相电压及基本空间矢量及其合成矢量在坐标轴下的分量(功率不变)
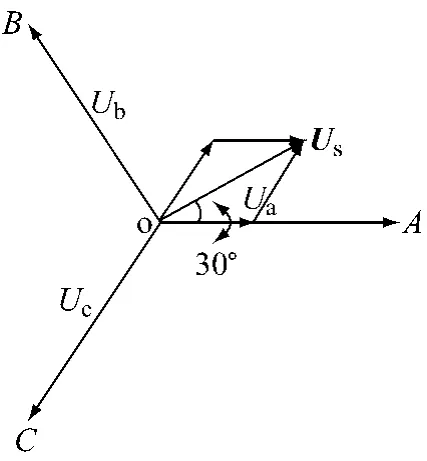
图6 状态110时的向量合成(ABC坐标系)
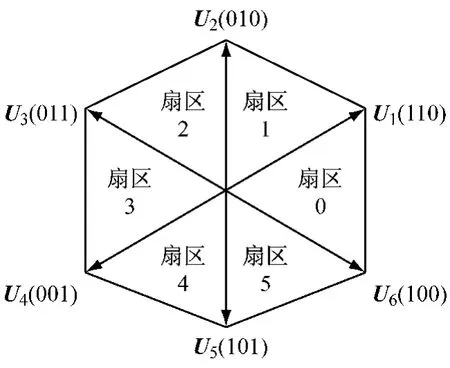
图7 △接法基本电压空间矢量及扇区划分
2 △接法扇区划分及扇区号确定
SVPWM控制中需要选用相邻的电压空间矢量合成所需要的输出电压矢量,并使其端点轨迹近似为圆形,从而使形成的磁链轨迹也接近于圆形。因此,首先需要判断所需电压的空间位置,即所处扇区,其次选用对应的基本电压空间矢量。电机Y及△接法两种情况下扇区划分不同,Y接法时扇区划分的方法不再适用于△接法。△接法时扇区的划分方法如下。
为计算和判断扇区方便,将ABC坐标系的各量转换到αβ两相静止坐标系中,取α轴与A相绕组的轴线重合,β轴超前α轴π/2。选择坐标变换前后的输出功率不变,则变换矩阵为
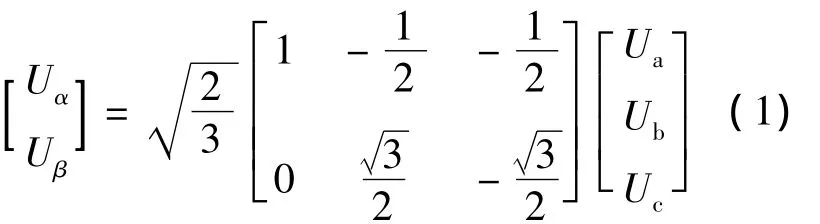
各开关状态对应△接法时的相电压(abc坐标)及其基本电压空间矢量在αβ坐标系的分量如表2所示。
确定扇区的方法有两种。
第一种,当输出电压以αβ坐标系上的分量形式Uα、Uβ给出时,先用式(2)计算B0、B1、B2:
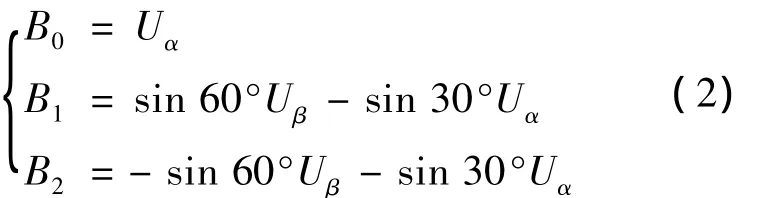
再用式(3)计算P值:
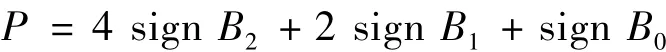
式中:sign(x)是符号函数。如果x>0,sign(x)=1;如果x<0,sign(x)=0。然后,根据P值查表 3即可确定扇区号。

表3 P值与扇区号的对应关系
第二种,当输出电压以幅值和相角的形式给出时,可直接根据相角来确定它所在的扇区。在实际系统中使用第一种更方便。
3 三角形接法存在的问题
SVPWM的实质是基波加三次谐波,当电机的绕组为三角形接法时,其电压中的三次谐波在绕组内部形成通路,造成环流。
图8、9分别为电机△接法且速度开环空载时的相电流及线电流波形,图10是Y接法且空载时的相电流波形。对比图8~10可见,与Y接法相比,△接法时不论是相电流还是线电流波形都存在着明显的谐波,使得电流波形发生畸变,且相电流比线电流的谐波含量更高。因此,在采用SVPWM方法时,电机绕组最好采用Y接法。
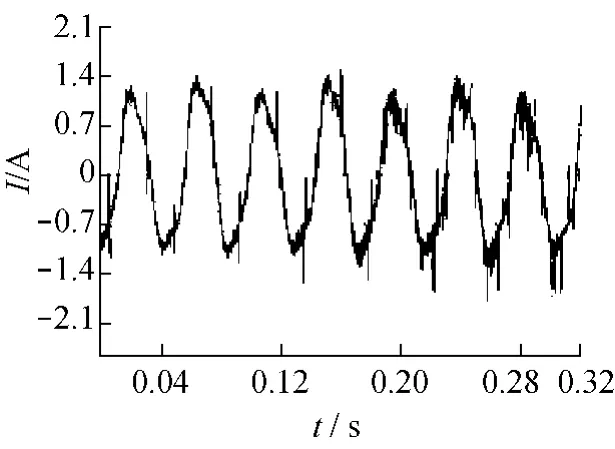
图8 △接时的相电流
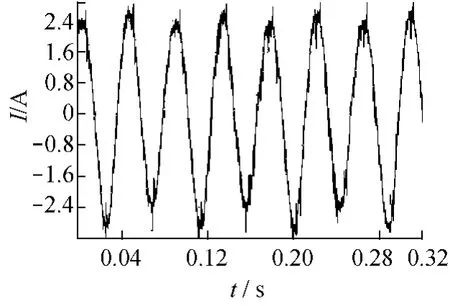
图9 △接时的线电流
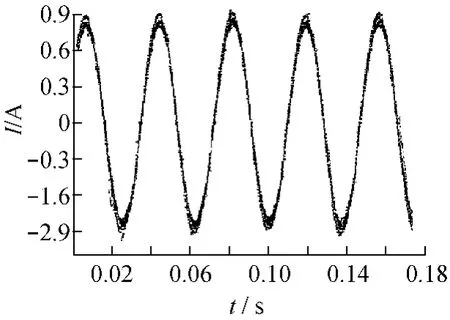
图10 Y接时的相电流
4 结语
本文从基本电压空间矢量的合成入手,分析了电机三角形接法和星型接法在采用SVPWM时的不同点,对两种接法下基本电压空间矢量的大小和相位做了详细说明,并在此基础上对三角形接法下空间矢量的扇区进行了重新划分,给出了扇区号的确定方法。
[1]王晓明,王玲.电动机的 DSP控制——TI公司的DSP应用[M].北京:北京航空航天大学出版社,2004.
[2]Satoshi Ogasawara.A novel PWM scheme of voltage source in-veters based on space vector theory[C]∥EPE Aachen,1989:1199-1202.
[3]TICorporation.TMS320LF240X Datasheet[G].2000.
[4]李波,安群涛,孙兵成.空间矢量脉宽调制的仿真研究及实现[J].电机与控制应用,2006,33(6):40-44.
[5]杨贵杰,孙丽,崔乃政,等.空间矢量脉宽调制技术的研究[J].中国电机工程学报,2001(5):226-231.
[6]郎宝华,刘卫国,周熙炜,等.空间矢量脉宽调制的仿真研究及应用[J].电机与控制应用,2007(34):6-9.
[7]李永东.交流电机数字控制系统[M].北京:机械工业出版社,2003.
